博弈论们：
-
Nim 博弈：
两个人以最优策略在玩游戏，有 \(n\) 堆石子，第 \(i\) 堆有 \(a_i\) 个，每人每次能从一堆石子中取任意多个石子但不能不取，不能拿的人输，请问先手与后手谁必胜？
-
先手，后手：第一个，第二个行动者。
-
必胜，必败：指先手必胜或必败。
-
定理：Nim 博弈先手必胜，当且仅当：$$\bigoplus_{i=1}^nA_i\ne 0$$
证明：反证法假设 \(A_i'=A_i\) 得出矛盾。（懒，咕了，有机会再说）
-
-
SG 函数
-
mex 运算：
对于一个非空数集: \(S\)
我们将 $$mex{ S }$$ 定义为不属于数集的最小非负整数，如 \(mex\{0,1,3\}\) 为 \(2\) 。 -
SG 函数：
对于每种可能状态的后继状态 \(y_i\)，我们将当前状态 \(x\) 的 SG 函数定义为：$$SG(x)=mex { SG(y_1),SG(y_2)......SG(y_n) }$$ -
SG 定理：
只有当：$$\bigoplus_{i=1}^n{SG_i}\ne 0$$
时，有先手必胜局面。
证明：放在有向图上，剩下基本一样。（懒，咕）
-
-
有向图游戏：
在一个有向无环图有一枚棋子，两个人轮流操纵棋子沿有向边移动，知道有一方不能移动后游戏结束，并此一方失败。
-
有向图游戏的和的 SG 函数值与其各子游戏的 SG 值的异或和相等。
-
有向图游戏必胜当且仅当当前局面的 SG 函数值大于 \(0\)。
-
有向图游戏必败当且仅当当前局面的 SG 函数值等于 \(0\)。
实际上任意的公平组合游戏均能转化成为有向图游戏，具体只要抽象出游戏的每个可能局面，以合法行动为局面之间连边。
-
-
威佐夫博弈：
两个人以最优策略在玩游戏，有 \(2\) 堆石子，每人每次可以拿走任意一堆中任意数量的石子或在两堆石子中拿走相同数量的石子，不能拿的人输，请问先手与后手谁必胜？
我们首先考虑必败局面，我们不妨将其称之为“奇异局面”，\((0,0)\) 与 \((1,2)\) 显然是一组“奇异局面” 那么我们考虑将这两种“奇异局面”中的一堆石子加减任意数，或同时加减任意数，得到“非奇异局面”，那便筛去了 \((k,2)\)，\((1,k)\)，\((0,k)\)，\((k,0)\)，\((k,k)\)，\((k,k+1)\) 这几种局面。
这样，我们就可以推出接下来的几种”奇异局面“：\[(0,0),(1,2),(3,5),(4,7),(6,10),(8,5)...... \]观察可知，”奇异局面“ \((x,y)\) 中，\(x\) 为前几种局面中数集取 \(mex\) 操作，而 \(y=x+k_{局面数}\)。
绘制函数，在坐标系中考虑，问题就抽象为了在坐标系中轮流进行游戏，每人可以向左（或向下）移动若干步，也可以向左下移动若干步，那我们把可以一步到达“奇异局面点”的坐标全部打标记，这些点均为“必胜局面”，如下：
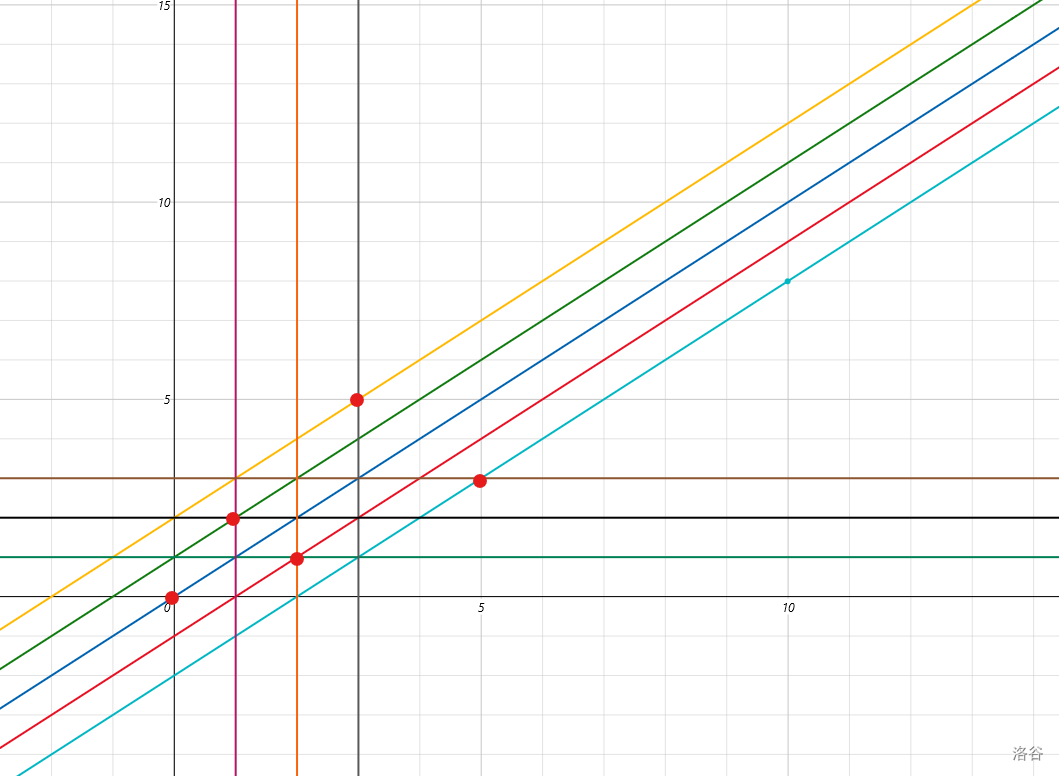
那么下一个“奇异局面”也就对应两个横纵坐标最小的未被染色的点。
-
beatty 定理：
设 \(a\)，\(b\) 是正无理数且 \(\frac{1}{a}+\frac{1}{b}=1\) 。记 \(P=\{\lfloor na\rfloor \mid n\in \mathbb N\}\)，\(Q=\{\lfloor nb \rfloor\mid n\in\mathbb N\}\)，则 \(P\) 与 \(Q\) 是 \(\mathbb N^+\) 的一个划分，即\(P\cap Q=\varnothing\) 且 \(P\cup Q=\mathbb N^+\)。（来自百度百科）
（不会证，但会用，先咕）
我们发现，相邻奇异局势的第一个数的差值是 \(1\) 或 \(2\) ,但分布过于玄学，所以我们可以认为第一个数被表示成 \(\lfloor an\rfloor\)，\(n\) 为任意正整数，\(a\) 为一无理数。我们将每种局面的前一个数与后一个数分别构成一个谱（\(Spec\)），可知它们满足 \(beatty\) 定理的条件，即构成自然数集的一个划分。
这样，第二个数可以被表示为\(\lfloor(a + 1)n\rfloor\)（已证）
根据 \(beatty\) 定理：
\[\frac{1}{a}+\frac{1}{a+1}=1 \]\[a^2-a-1=0 \]解得：
\[a=\frac{1\pm\sqrt 5}{2} \]我们取 \(a=\frac{1+\sqrt 5}{2}\) 为根，这显然是黄金分割比，因此，我们就得到了两“奇异局面”数之间的关系。
-
-
斐波那契博弈：
两个人在以最优策略玩游戏，有一堆石子，先手第一次可以拿任意多个但不能全拿走也不能不拿，之后每个人最少拿一个，最多拿前一个人两倍那么多个，谁取到最后一个谁就能获胜，请问先手后手谁必胜？
先不去考虑正解证明，我们来大力手玩一下（\(n=1\) 不做考虑）：
-
当 \(n=2\) 时，显然有先手必败。
-
当 \(n=3\) 时，先手不论抓几个，均面临必败局面。
-
当 \(n=4\) 时，先手以最优策略抓一个，后手至多只能抓两个，局面向 \(n=3\) 连边。
-
当 \(n=5\) 时，先手不论抓几个，后手均能将当前局面连向前局面，先手必败。
-
当 \(n=6\) 时，先手以最优策略抓一个，则当前局面向 \(n=5\) 连边，先手必胜。
\(\cdots\)
我们似乎可以得出：如当前石子数为斐波那契数，则当前局面先手必败。
正确否？
我们考虑证明，但那之前，先看这样一个定理：
-
Zeckendorf 定理：
对于任意一个正整数 \(n\)，都可以视作若干个不相邻的斐波那契数之和。
证明（我不会）
知道了它，我们开始证明：
- 假设当前石子数为斐波那契数 \(f_i\)，那么 \(f_i\) 一定可以拆分为 \(f_{i-1}+f_{i-2}\) 的形式，现在假设所取石子数小于等于 \(\frac{f_i}{3}\) 那么必然先手失败，若取得石子数大于了 \(\frac{f_i}{3}\) 显然此时先手必败。
- 假设当前石子数为非斐波那契数，利用 \(Zeckendorf\) 定理，那么先手的策略是：拆分后取走最小的斐波那契数，后手面对下一个斐波那契数没有办法一次取走，取完这个部分的仍旧是先手，依次直到石子全部取走。先手必胜。
-
