走迷宫(可使用激光)
题目描述:
给定一个 n×m 的迷宫,迷宫由 "#" 与"." 两种字符组成。其中 "#" 代表障碍物,"." 表示空地。迷宫中还有一个起点 "S" 和一个终点 "E" ,它们都可以视为空地。
由于近期迷宫发生了塌方,导致起点和终点之间可能并不连通。幸运的是,你拥有一种超能力——在迷宫中移动时(移动方向为上、下、左、右四个方向之一),可以在当前位置朝任一方向(上、下、左、右四个方向之一)释放激光。激光能够清除该方向上所有的障碍物,并且这种超能力至多只能使用一次。
现在,你需要判断是否能利用这种超能力成功从起点到达终点。
输入描述:
第一行给定两个正整数n,m,(2<=n,m<=1000),分别表示迷宫的行数和列数。
下面 n 行,每行 m 个字符,描述迷宫的具体布局。字符只包含 "#"、"."、"S" 和 "E",并且起点与终点有且仅有一个。
输出描述:
能够到达终点输出 YES ;否则输出 NO
思路1:使用DFS暴力搜索,在搜索的过程中一但遇到障碍物就使用激光,然后接着搜索.
#include<bits/stdc++.h>
using namespace std;
int m,n;
char maz3[1010][1010];//这个是迷宫
bool visited[1010][1010];//判断走过的地方防止无限递归
int sx,sy,ex,ey;//起始点和终止点
//使用激光清除障碍物,为了方便撤回操作,使用感叹号代替障碍物
void usetrick(int x,int y,int dir){
while(0 <= x and 0 <= y and x < m and y < n){
if(maz3[x][y] == '#') maz3[x][y] = '!';
if(dir == 0) x--;
if(dir == 1) y++;
if(dir == 2) x++;
if(dir == 3) y--;
}
}
void unusetrick(int x,int y,int dir){
while(0 <= x and 0 <= y and x < m and y < n){
if(maz3[x][y] == '!') maz3[x][y] = '#';
if(dir == 0) x--;
if(dir == 1) y++;
if(dir == 2) x++;
if(dir == 3) y--;
}
}
//DFS递归搜索
bool ch3ck(bool trick,int x,int y){
if(x == ex and y == ey) return true;
bool flag = false;//能不能走到E点
for(int i=0;i<4;++i){//四个方向
int nx = x,ny = y;//现在的坐标
if(i == 0) nx--;
if(i == 1) ny++;
if(i == 2) nx++;
if(i == 3) ny--;
if(0 <= nx and 0 <= ny and nx < m and ny < n and !visited[nx][ny]){//没走过并且在迷宫内
visited[nx][ny] = true;
if(maz3[nx][ny] != '#'){//不是障碍物的话就往个下走
if(ch3ck(trick,nx,ny)) flag = true;
}
else if(trick){//如果是障碍物就清除并且标记使用了trick,trick在之后的递归就不能用了
trick = false;
usetrick(x,y,i);
if(ch3ck(trick,nx,ny)) flag = true;
unusetrick(x,y,i);
trick = true;//这两行是递归回溯
}
visited[nx][ny] = false;
}
}
return flag;
}
int main(){
cin >> m >> n;
for(int i=0;i<m;++i){
for(int j=0;j<n;++j){
char ch;
cin >> ch;
maz3[i][j] = ch;
if(ch == 'S'){
sx = i;
sy = j;
}
if(ch == 'E'){
ex = i;
ey = j;
}
}
}
bool trick = true;
if(ch3ck(trick,sx,sy)){
cout << "YES";
}
else{
cout << "NO";
}
return 0;
}
由于该算法的复杂度为O(n*n*m*m),显然超时了(10^12)
思路2:使用队列BFS代替递归DFS
#include<bits/stdc++.h>
using namespace std;
int m,n;
char maz3[1010][1010];
bool visited[1010][1010];
int sx,sy,ex,ey;
void usetrick(int x,int y,int dir){
while(0 <= x and 0 <= y and x < m and y < n){
if(maz3[x][y] == '#') maz3[x][y] = '!';
if(dir == 0) x--;
if(dir == 1) y++;
if(dir == 2) x++;
if(dir == 3) y--;
}
}
void unusetrick(int x,int y,int dir){
while(0 <= x and 0 <= y and x < m and y < n){
if(maz3[x][y] == '!') maz3[x][y] = '#';
if(dir == 0) x--;
if(dir == 1) y++;
if(dir == 2) x++;
if(dir == 3) y--;
}
}
bool check(int x,int y){
int dx[] = {-1,0,1,0};
int dy[] = {0,1,0,-1};
queue<pair<int,int>> q;
q.push({x,y});
visited[x][y] = true;
while(!q.empty()){
pair<int,int> pnow = q.front();q.pop();
int x = pnow.first,y = pnow.second;
if(x == ex and y == ey) return true;
for(int i=0;i<4;++i){//四个方向
int nx = x+dx[i],ny = y+dy[i];
if(nx >= 0 and ny >= 0 and nx < m and ny < n){
if(maz3[nx][ny] != '#' and !visited[nx][ny]){
visited[nx][ny] = true;
q.push({nx,ny});
}
}
}
}
return false;
}
bool ch3ck(){
int dx[] = {-1,0,1,0};
int dy[] = {0,1,0,-1};
queue<pair<int,int>> q;
q.push({sx,sy});
visited[sx][sy] = true;
while(!q.empty()){
pair<int,int> pnow = q.front();q.pop();
int x = pnow.first,y = pnow.second;
if(x == ex and y == ey) return true;
for(int i=0;i<4;++i){//四个方向
int nx = x+dx[i],ny = y+dy[i];
if(nx >= 0 and ny >= 0 and nx < m and ny < n){
if(maz3[nx][ny] != '#' and !visited[nx][ny]){
visited[nx][ny] = true;
q.push({nx,ny});
}
else{
usetrick(nx,ny,i);
bool visitedTmp[1010][1010];
memcpy(visitedTmp,visited,sizeof(visited));
if(check(nx,ny)) return true;
memcpy(visited,visitedTmp,sizeof(visited));
unusetrick(nx,ny,i);
}
}
}
}
return false;
}
int main(){
cin >> m >> n;
for(int i=0;i<m;++i){
for(int j=0;j<n;++j){
char ch;
cin >> ch;
maz3[i][j] = ch;
if(ch == 'S'){
sx = i;
sy = j;
}
if(ch == 'E'){
ex = i;
ey = j;
}
}
}
if(ch3ck()){
cout << "YES";
}
else{
cout << "NO";
}
return 0;
}
在ch3ck函数中若使用激光,进入check函数搜索,虽然这两个函数都是O(m*n),但嵌套之后跟上一个代码复杂度是一样的.
思路3:从起点和重点分别做BFS搜索,找出从起点和重点能到达的地方,这一部分的复杂度是O(2*m*n) = O(m*n)
做完这一部分之后,存入两个二维数组里,方便后续工作.
例如:
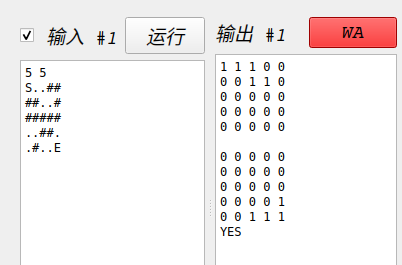
很直接的能想到,如果在这个5*5迷宫里有横的一条线或者竖的一条线,这线上既有S能到的地方,又有E能到的地方,不就是能到达吗(使用激光).或者是更简单的情况不使用激光也能到达.
但是使用激光后开出来的路可能从两边走可能到达终点!!
所以解法是在比较时同时比较S能到达的一条线和E能到达的三条线
AC代码如下:
#include<bits/stdc++.h>
using namespace std;
int m,n,sx,sy,ex,ey;
int maz3[1010][1010][3];
void chSck(){
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
queue<pair<int,int>> q;
q.push({sx,sy});
maz3[sx][sy][1] = 1;
while(!q.empty()){
int x = q.front().first,y = q.front().second;q.pop();
for(int i=0;i<4;++i){
int nx = x+dx[i],ny = y+dy[i];
if(nx >= 0 and ny >= 0 and nx < m and ny < n){
if(maz3[nx][ny][0] != '#' and !maz3[nx][ny][1]){
maz3[nx][ny][1] = 1;
q.push({nx,ny});
}
}
}
}
}
void chEck(){
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
queue<pair<int,int>> q;
q.push({ex,ey});
maz3[ex][ey][2] = 1;
while(!q.empty()){
int x = q.front().first,y = q.front().second;q.pop();
for(int i=0;i<4;++i){
int nx = x+dx[i],ny = y+dy[i];
if(nx >= 0 and ny >= 0 and nx < m and ny < n){
if(maz3[nx][ny][0] != '#' and !maz3[nx][ny][2]){
maz3[nx][ny][2] = 1;
q.push({nx,ny});
}
}
}
}
}
bool ch3ck(){
for(int i=0;i<m;++i){
int ToS = 0;
int ToE = 0;
for(int j=0;j<n;++j){
ToS += maz3[i][j][1];
ToE += maz3[i][j][2];
if(i>0)ToE += maz3[i-1][j][2];
if(i<m-1)ToE += maz3[i+1][j][2];
}
if(ToS and ToE) return true;
}
for(int j=0;j<n;++j){
int ToS = 0;
int ToE = 0;
for(int i=0;i<m;++i){
ToS += maz3[i][j][1];
ToE += maz3[i][j][2];
if(j>0)ToE += maz3[i][j-1][2];
if(j<n-1)ToE += maz3[i][j+1][2];
}
if(ToS and ToE) return true;
}
return false;
}
int main(){
cin >> m >> n;
for(int i=0;i<m;++i){
for(int j=0;j<n;++j){
char ch;
cin >> ch;
maz3[i][j][0] = ch;
if(ch == 'S'){
sx = i;
sy = j;
}
if(ch == 'E'){
ex = i;
ey = j;
}
}
}
chEck();
chSck();
// for(int i=0;i<m;++i){
// for(int j=0;j<n;++j){
// cout << maz3[i][j][1] << ' ';
// }
// cout << endl;
// }
// cout << endl;
// for(int i=0;i<m;++i){
// for(int j=0;j<n;++j){
// cout << maz3[i][j][2] << ' ';
// }
// cout << endl;
// }
if(ch3ck()) cout << "YES";
else cout << "NO";
return 0;
}





