二分查找时间复杂度推导

　　二分查找是一个非常常用且简洁的查找算法，相信很多人也知道它的时间复杂度是logN，但是我看网上的大多数博客给出的所谓推导过程都十分不严谨，于是我花了些时间自己写了推导过程。

首先上二分查找的代码：

    public int find(int x, int[] data) {
        return find(x, data, 0, data.length - 1);
    }

    /**
     * 查找元素下标，没找到返回-1
     * @param x 待查找元素
     * @param data 有序的元素数组
     * @createTime：2017年3月4日 
     * @author: gaojiabao
     */
    private int find(int x, int[] data, int low, int high) {
        int mid = (low + high) >> 1;
        if (x == data[mid]) {
            return mid;
        } else if (x > data[mid]) {
            low = mid + 1;
        } else if (x < data[mid]) {
            high = mid - 1;
        }

        if (low == high) {
            if (x == data[low]) {
                return low;
            } else {
                return -1;
            }
        } else {
            return find(x, data, low, high);
        }
    }

下面是推导过程：

假设数据的规模为N(即每次调用时的high-low)，程序执行的比较次数表示为C(N)，假设程序查找的是一个不存在的数据，则此时执行的次数是最多的：

执行第一次时，有：

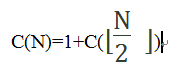
1代表执行了一次x和data[mid]的比较过程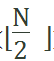，代表下一次递归调用find方法时high-low的值，也就是新的数据规模每次较少一半以上。

递归上面的公式，有：

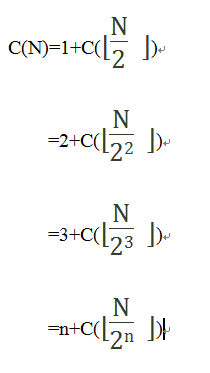
我们知道每一个整数都可以表示为2ⁱ+k的形式，如1=2⁰+0，5=2²+1，10=2³+2，因此

设N=2ⁱ+k

令上面公式的n=i，则有：

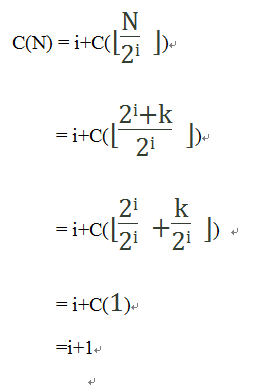
因为N=2ⁱ+k，则有i=⌊lgN⌋，因此：

 

 

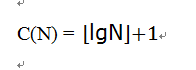
因为我们一直以来的假设是要查找到的元素是找不到的，所以现在的情况是C(N)最大的情况，对于一般情况，则有：

 

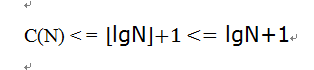
因此二分查找的时间复杂度是logN。