LCA学习笔记

目录

1. 前言
2. LCA简介
3. 倍增求LCA
4. 树剖求LCA
5. LCA在树形结构题中的妙用

1.前言

应老师要求，来写一篇关于LCA的学习笔记

2.LCA简介

两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。
画张图理解一下：

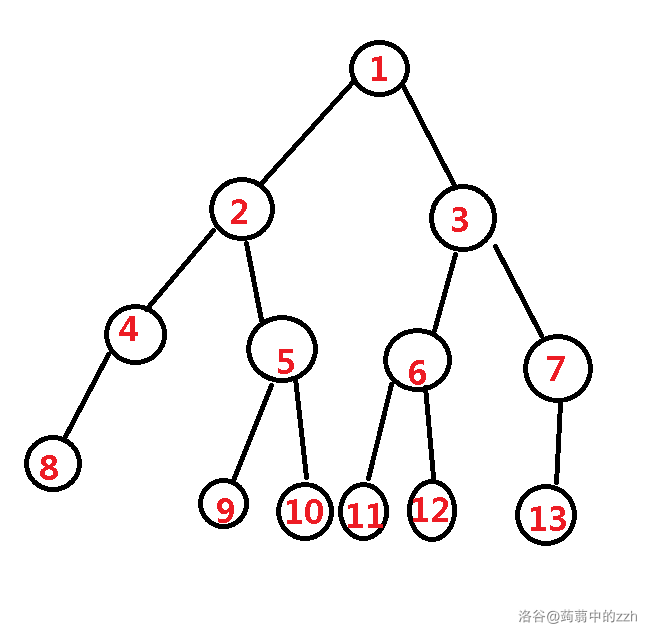
如图，10与8的LCA是2，13与3的LCA是3
那么怎么求LCA呢？

3.倍增求LCA

想到求LCA，我们极易想到一个朴素算法：
每次找深度比较大的那个点，让它向上跳。显然在树上，这两个点最后一定会相遇，相遇的位置就是想要求的 LCA。
在最坏情况下，朴素算法每次查询的时间为 \(\mathcal{O}(n)\)，显然不行。
这时候我们可以用倍增算法。
倍增算法是最经典的 LCA 求法，是朴素算法的改进算法。
倍增算法的思想是：预处理 \(fa[x][i]\) ，表示 \(x\) 的第 \(2^i\) 个祖先。
先将要求节点 \(u,v\) 跳转到同一高度
然后如果 \(fa[u][i] ≠ fa[v][i]\) ，则 \(u=fa[u][i]\) ，\(v=fa[v][i]\)
结果为 \(fa[u][0]\) 。
代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5000007;
struct node
{
	int to,next;
}edge[N];
int n,m,fa[N][101],s,dep[N],head[N],lg[N],cnt;
void add(int a,int b)
{
	edge[++cnt].to=b;
	edge[cnt].next=head[a];
	head[a]=cnt;
}
void dfs(int x,int y)
{
	fa[x][0]=y;
	dep[x]=dep[y]+1;
	for(int i=1;i<=lg[dep[x]];i++)
		fa[x][i]=fa[fa[x][i-1]][i-1];
	for(int i=head[x];i;i=edge[i].next)
		if(edge[i].to!=y)
			dfs(edge[i].to,x);
}
int lca(int x,int y)
{
	if(dep[x]<dep[y]) swap(x,y);
	while(dep[x]>dep[y]) x=fa[x][lg[dep[x]-dep[y]]-1];
	if(x==y) return x;
	for(int i=lg[dep[x]]-1;i>=0;i--)
		if(fa[x][i]!=fa[y][i])
			x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}
int main()
{
	cin>>n>>m>>s;
	for(int i=1;i<=n-1;i++)
	{
		int x,y;
		cin>>x>>y;
		add(x,y);
		add(y,x);
	}
	for(int i=1;i<=n;i++)
		lg[i]=lg[i-1]+(1<<lg[i-1]==i);
	dfs(s,0);
	while(m--)
	{
		int x,y;
		cin>>x>>y;
		cout<<lca(x,y)<<endl;
	}
	return 0;
}

4.树剖求LCA

与倍增求 LCA 类似，树剖求LCA是每次跳到所在重链的顶端，当跳到同一条重链上时，深度较小的结点即为 LCA。
要注意的是，向上跳重链时需要先跳所在重链顶端深度较大的那个。
代码：

#include<bits/stdc++.h>
#define ll long long
#define endl "\n"
using namespace std;
const int N=5e6+7;
struct edge
{
	int to,nxt;
}e[N];
int head[N],cnt;
void add(int u,int v)
{
	e[++cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
int n,m,s;
int fa[N],siz[N],son[N],dfn[N],id[N],top[N],dep[N];
void dfs1(int x)
{
	dep[x]=dep[fa[x]]+1;
	siz[x]=1;
	for(int i=head[x];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa[x]) continue;
		fa[v]=x;
		dfs1(v);
		siz[x]+=siz[v];
		if(!son[x]||siz[x]>siz[son[x]])
			son[x]=v;
	}
	return ;
}
int cnt1;
void dfs2(int x,int d)
{
	top[x]=d;
	dfn[x]=++cnt1;
	id[dfn[x]]=x;
	if(son[x]) dfs2(son[x],d);
	for(int i=head[x];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(fa[x]!=v&&son[x]!=v)
			dfs2(v,v);
	}
}
int LCA(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]>dep[top[y]]) x=fa[top[x]];
		else y=fa[top[y]];
	}
	if(dep[x]<dep[y]) return x;
	else return y;
}
int main()
{
	cin>>n>>m>>s;
	for(int i=1;i<n;i++)
	{
		int x,y;
		cin>>x>>y;
		add(x,y);
		add(y,x);
	}
	dfs1(s);
	dfs2(s,s);
	while(m--)
	{
		int x,y;
		cin>>x>>y;
		cout<<LCA(x,y)<<endl;
	}
	return 0;
}

5.LCA在树形结构题中的妙用

LCA最大的用处就是：求路径。
在一棵树上，\(u\) 到 \(v\) 的路径一定是 \(u\rightarrow LCA(u,v)\rightarrow v\)
这个性质可以帮我们解决很多题，也可以与树上差分结合。