线段树学习笔记（入门）

目录

1. 前言
2. 线段树基础
   2.1 定义
   2.2 区间操作和懒标记
   2.3 一些例题

1.前言

应老师要求，来写一篇关于线段树的学习笔记

2.线段树基础

2.1 定义

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
差不多就长这样子：

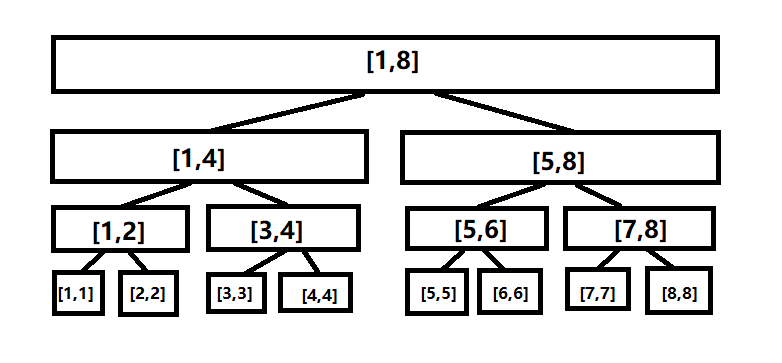
我们可以用它来维护区间信息。

2.2 区间操作和懒标记

建树
我们用数组 \(t\) 来保存线段树。\(t[i]\) 代表线段树第 \(i\) 个节点的值。
极易发现，第 \(i\) 个节点的左儿子和右儿子分别为 \(i*2\) 和 \(i*2+1\)
于是我们就可以建树了

void build(int x,int l,int r)
{
	if(l==r)
	{
		t[x]=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(x*2,l,mid);
	build(x*2,mid+1,r);
	push_up(x);
}

其中 push_up 是维护父节点与子节点的关系的，里面具体写什么要看你的线段树要维护什么。
区间查询
其实就是用分块+二分的思想。
用上面那个图。假如我们要查 \([1,4]\) ，那可以直接返回 \([1,4]\) 的值
假入要查 \([4,7]\) ，那就要把 \([4,7]\) 分为 \([4,4]，[5,6]\) 与 \([7,7]\) ，再查询。
时间复杂度为 \(\mathcal{O}(\text{log}_2n)\)
代码是求区间和的

ll sum(ll x,ll l,ll r,ll L,ll R)
{
	ll mid=(l+r)/2;
	if(l>=L&&r<=R) return t[x];
	ll ans=0;
	if(mid>=L) ans=(ans+sum(x*2,l,mid,L,R))%p;
	if(mid<R) ans=(ans+sum(x*2+1,mid+1,r,L,R))%p;
	return ans;
}

区间修改
最原始的区间修改和区间查询差不多。代码不放了。
但是假如有过多的修改操作，原始的区间修改时间复杂度就过大了，一次修改复杂度可能会有 \(\mathcal{O}(n)\)。
这时我们可以引入一个新概念：懒标记
意思就是给一个线段树上的节点打一个标记，意思就是这个节点已经修改，但它的子节点还没有修改。
当要对这个节点进行查询的时候再进行修改，可以大大降低时间复杂度。
而且这个懒标记是可以累积的。

2.3 一些例题

P3372 【模板】线段树 2
就是上面讲的。要注意懒标记要先乘后加

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,p;
const int N=100000+7;
ll a[N],t[N*4],lj[N*4],lc[N*4];
void build(ll x,ll l,ll r)//mei
{
	lc[x]=1;
	if(l==r)
	{
		t[x]=a[l]%p;
		return ;
	}
	int mid=l+r>>1;
	build(x<<1,l,mid);
	build(x<<1|1,mid+1,r);
	t[x]=(t[x<<1]+t[x<<1|1])%p;
	return ;
}
void pushdown(ll x,ll l,ll r)//mei
{
	int mid=l+r>>1;
	t[x<<1]=(t[x<<1]*lc[x]+lj[x]*(mid-l+1))%p;
	t[x<<1|1]=(t[x<<1|1]*lc[x]+lj[x]*(r-mid))%p;
	lj[x<<1]=(lj[x<<1]*lc[x]+lj[x])%p;
	lj[x<<1|1]=(lj[x<<1|1]*lc[x]+lj[x])%p;
	lc[x<<1]=lc[x<<1]*lc[x]%p;
	lc[x<<1|1]=lc[x<<1|1]*lc[x]%p;
	lj[x]=0;
	lc[x]=1;
	return ;
}
void add(ll x,ll l,ll r,ll L,ll R,ll k)//mei
{
	if(l>=L&&r<=R)
	{
		t[x]=(t[x]+(r-l+1)*k)%p;
		lj[x]=(lj[x]+k)%p;
		return ;
	}
	pushdown(x,l,r);
	ll mid=(l+r)/2;
	if(mid>=L) add(x*2,l,mid,L,R,k);
	if(mid<R) add(x*2+1,mid+1,r,L,R,k);
	t[x]=t[x*2]+t[x*2+1];	
	t[x]%=p;
}
void mul(ll x,ll l,ll r,ll L,ll R,ll k)
{
	if(l>=L&&r<=R)
	{
		t[x]*=k;
		t[x]%=p;
		lj[x]=(lj[x]*k)%p;
		lc[x]=(lc[x]*k)%p;
		return ;
	}
	pushdown(x,l,r);
	ll mid=(l+r)/2;
	if(mid>=L) mul(x*2,l,mid,L,R,k);
	if(mid<R) mul(x*2+1,mid+1,r,L,R,k);
	t[x]=t[x*2]+t[x*2+1];
	t[x]%=p;
}
ll sum(ll x,ll l,ll r,ll L,ll R)
{
	ll mid=(l+r)/2;
	if(l>=L&&r<=R) return t[x];
	ll ans=0;
	pushdown(x,l,r);
	if(mid>=L) ans=(ans+sum(x*2,l,mid,L,R))%p;
	if(mid<R) ans=(ans+sum(x*2+1,mid+1,r,L,R))%p;
	return ans;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n>>m>>p;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	build(1,1,n);
	for(int i=1;i<=m;i++)
	{
		int op;
		cin>>op;
		if(op==1)
		{
			int x,y,k;
			cin>>x>>y>>k;
			mul(1,1,n,x,y,k);
		}
		if(op==2)
		{
			int x,y,k;
			cin>>x>>y>>k;
			add(1,1,n,x,y,k);
		}
		if(op==3)
		{
			int x,y;
			cin>>x>>y;
			cout<<sum(1,1,n,x,y)<<endl;
		}
	}
	return 0;
}

P4588 [TJOI2018]数学计算
有点思维的线段树题。可以把题目转化一下，就会变成：修改一个值，查询之前的某个值。
可以建线段树，维护区间乘，于是根节点就是所有数的乘积
最后输出根节点%mod即可。

#include<bits/stdc++.h>
#define ll long long
#define endl "\n"
using namespace std;
const int N=1e7+7;
ll t[N],mod;
void push_up(int x)
{
	t[x]=(t[x*2]*t[x*2+1])%mod;
}
void build(int x,int l,int r)
{
	if(l==r)
	{
		t[x]=1;
		return ;
	}
	int mid=(l+r)>>1;
	build(x*2,l,mid);
	build(x*2+1,mid+1,r);
	push_up(x);
}
void change(int x,int l,int r,int X,int k)
{
	if(l==r)
	{
		t[x]=k;
		return ;
	}
	int mid=(l+r)>>1;
	if(X<=mid) change(x*2,l,mid,X,k);
	if(X>mid) change(x*2+1,mid+1,r,X,k);
	push_up(x);
}
int main()
{
	int tt;
	cin>>tt;
	while(tt--)
	{
		int n,op,m;
		cin>>n>>mod;
		build(1,1,n);
		for(int i=1;i<=n;i++)
		{
			cin>>op>>m;
			if(op==1) change(1,1,n,i,m);
			else change(1,1,n,m,1);
			cout<<t[1]%mod<<endl;
		}
	}
    return 0;
}

P4145 上帝造题的七分钟 2 / 花神游历各国
线段树裸题
注意到如果数字是 \(1/0\) ，那么开方没有任何意义。
所以可以维护区间最值与区间和，如果区间最值为1/0，那么直接跳过修改操作。
最后就是个裸的板子1了。
记得开 long long

#include<bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;
const int N=1e5+7;
int a[N],t[N*4],maxx[N*4];
int n,m;
void push_up(int x)
{
	t[x]=t[x*2]+t[x*2+1];
	maxx[x]=max(maxx[x*2],maxx[x*2+1]);
}
void build(int x,int l,int r)
{
	if(l==r)
	{
		maxx[x]=t[x]=a[l];
		return ;
	} 
	int mid=(l+r)>>1;
	build(x*2,l,mid);
	build(x*2+1,mid+1,r);
	push_up(x);
}
void change(int x,int l,int r,int L,int R)
{
	if(maxx[x]<=1) return ;
	if(l==r)
	{
		maxx[x]=t[x]=sqrt(t[x]);
		return ;
	}
	int mid=(l+r)/2;
	if(L<=mid) change(x*2,l,mid,L,R);
	if(R>mid) change(x*2+1,mid+1,r,L,R);
	push_up(x); 
}
int query(int x,int l,int r,int L,int R)
{
	if(l>=L&&r<=R)
		return t[x];
	int mid=(l+r)/2;
	int ans=0;
	if(L<=mid) ans+=query(x*2,l,mid,L,R);
	if(R>mid) ans+=query(x*2+1,mid+1,r,L,R);
	return ans;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	cin>>m;
	build(1,1,n);
	while(m--)
	{
		int op,l,r;
		cin>>op>>l>>r;
		if(l>r) swap(l,r);
		if(op==0)
			change(1,1,n,l,r);
		else
			cout<<query(1,1,n,l,r)<<endl;
	}
	return 0;
}