ConvReLU++@MobiSys'23

ConvReLU++ Reference-based Lossless Acceleration of Conv-ReLU Operations on Mobile CPU

1 核心问题

为了优化边缘设备上的 CNN 推理，我们寻求一个机会来节省 ReLU 的计算和延迟。ReLU 是一种广泛使用的 CNN 激活函数，因为它具有实用性。Conv-ReLU（卷积层后跟 ReLU 激活）结构的一个很好的特性是其高输出稀疏性，即 Conv-ReLU 的输出可能包含大部分零。具体来说，ReLU 激活函数会将卷积层输出中的所有负值转换为零。这意味着在卷积操作中获取精确负值的计算成本可能会被浪费。尽管这种浪费的计算可能不会在密集矩阵运算高度优化的高性能机器上产生太多开销，但在资源有限的边缘和移动设备上却可能很大。

1.1 实验观察

我们的方法基于这样的洞察：判断向量乘法操作的输出是否为负数可能比实际执行该操作更快。因此，在 ReLU 激活之前的向量乘法操作可以被跳过，如果它们的输出值预计为负数。我们将这种在没有实际计算的情况下预测负值输出的情况称为预测输出稀疏性。具体来说，在常见的 Conv-ReLU 结构中，卷积滤波器与其感受野之间的交互是一个向量乘法操作，可以应用优化。同时，移动 CPU 上有限的并行性和灵活的指令集使得通过跳过这些负输出计算实际加速成为可能。

1.2 其他工作的问题

先前的工作提出了各种方法来识别和跳过这种冗余乘法[6,24,46,53,56]，但它们要么是有损的，要么仅适用于特定场景（例如，对视频内容的连续推理）。在可预见的输出稀疏性下实现通用视觉任务加速的关键是识别具有低开销和高成功率的负输出操作。

1.3 思想

我们引入了一种基于参考的方法，用于识别和减少一般视觉任务的 Conv-ReLU 结构中不必要的向量乘法。

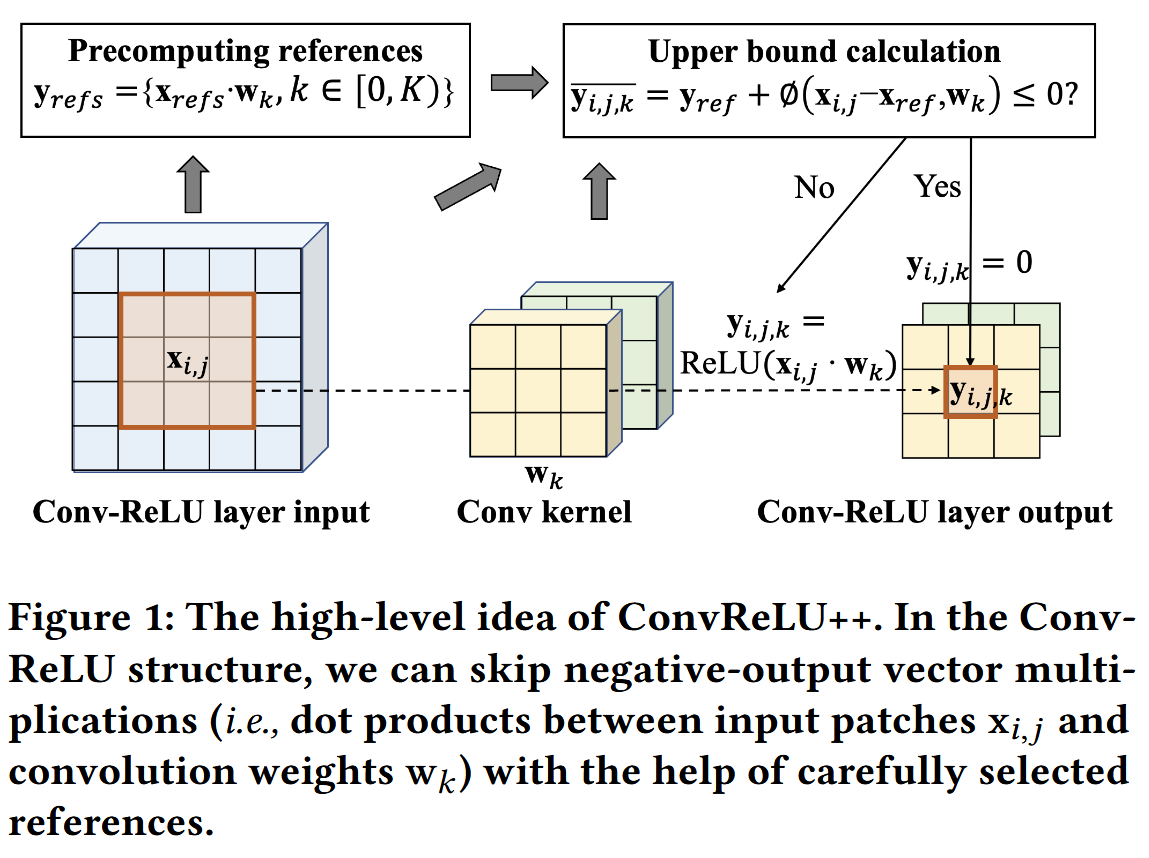
首先，给定一个 Conv 内核及其要相乘的输入补丁（patch，局部区域），我们执行基于哈希的快速聚类，以获得一组在特征图中具有代表性的参考补丁。参考补丁和 Conv 内核之间的点积结果是预先计算好的，以便以后进行比较。然后，我们通过将 Conv 内核和其他输入补丁与参考补丁进行比较来计算点积的紧密上限。最后，我们识别不必要的（负输出）乘法运算，并在卷积运算中跳过它们，以降低计算成本。图 1 说明了这一高级思想。所有步骤都设计为与矢量级并行兼容，矢量级并行性可以在移动平台（例如 ARM NEON）上利用高级 SIMD 内部函数。

2 观察与分析

2.1 Conv-ReLU 结构

Conv-ReLU 结构（即卷积层后跟 ReLU 激活）在流行的 CNN 模型中很常见，用于将输入图像或特征图转换为更高级别的特征。

假设$l_{\textbf{W}}$是 2D 卷积层，卷积层的输入特征图$\textbf{x}$。2D 卷积权重$\textbf{W} \in \mathbb{R}^{R\times S \times C \times K}$，偏置$\textbf{b}\in \mathbb{R}^K$，其中$R\times S$表示卷积核大小，$C$ 和 $K$ 分别表示输出输出通道数。我们使用$\textbf{y}$表示 Conv-ReLU 层的输出。那么$\textbf{y}$的$(i,j)$位置的第$k$个通道的输出值可以表示为:

\[\begin{align*} y_{i,j,k} & =\text{ReLU}(\text{Conv}(\textbf{x},\textbf{W})) \\ & = \text{ReLU}(\textbf{x}_{i,j}\cdot \textbf{w}_{k}) \\ & = \text{ReLU} \bigg(\sum_{r=0}^{R-1}{\sum_{s=0}^{S-1}{\sum_{c=0}^{C-1}{\textbf{x}_{i+r,j+s,c}\cdot \textbf{W}_{r,s,c,k}+\textbf{b}_{k}}}}\bigg) \end{align*} \]

其中$\textbf{x}_{i,j}$ 和 $\textbf{w}_{k}$是子矩阵的平铺向量。这样就卷积的矩阵乘转为向量点积了。我们在$\textbf{x}_{i,j}$尾部添加 1 和 $\textbf{w}_{k}$尾部添加$\textbf{b}_{k}$来额外计算偏置。

\[\begin{align*} \textbf{x}_{i,j}&=[\textbf{x}_{i,j,0},\textbf{x}_{i,j,1},\cdots,\textbf{x}_{i+R-1,j+S-1,C-1},1] \\ \textbf{w}_{k} &= [\textbf{W}_{0,0,0,k},\textbf{W}_{0,0,1,k},\cdots,\textbf{W}_{R-1,S-1,C-1,k}, \textbf{b}_{k}] \end{align*} \]

因此，Conv-ReLU 结构中的整个计算可以看作是长向量乘法，每个乘法计算 y 中的一个元素，然后是将所有负积转换为零的 ReLU 操作。由于向量乘法是相互独立的，因此它们可以在多处理器架构上并行执行。

2.2 Conv-ReLU 的数据特点

输出高度稀疏.
根据 2.1 的推导，计算卷积层输出$\textbf{y}$的每一个元素$\textbf{y}_{i,j,k}$需要两个长向量的点乘。如果$\textbf{y}_{i,j,k}$是负数的话，其实不需要精确的计算$\textbf{y}_{i,j,k}$的值。如果能够以很低的成本从$\textbf{x}_{i,j}$ 和 $\textbf{w}_{k}$中推断出$\textbf{y}_{i,j,k}$正负值，那么就可以减少$\textbf{x}_{i,j}\cdot \textbf{w}_{k}$的计算次数。

为此，作者在图 2 中展示浮点运算中非 0 输出和 0 输出的比率。他们随机使用 5000 张 ImageNet 的图像数据喂给 VGG-16 的 Conv-ReLU 层。

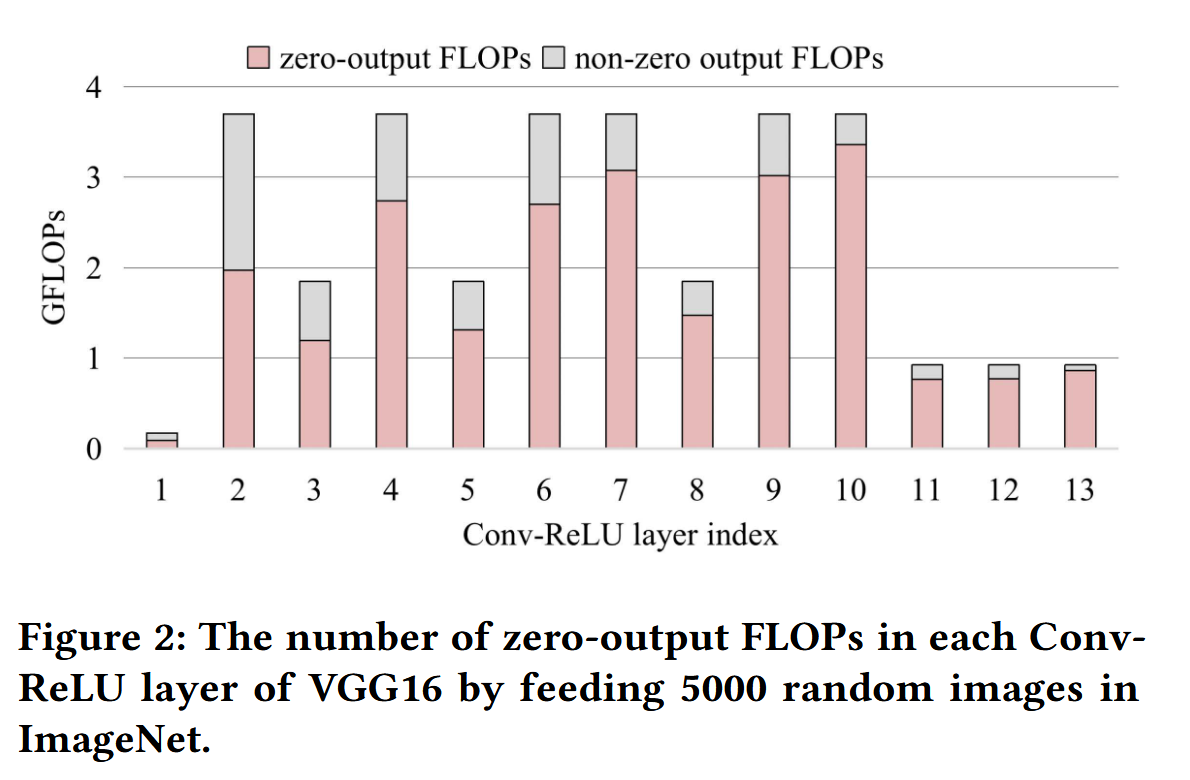
我们发现，在每一个 Conv-ReLU 的计算量中，存在大量的计算输出了 0。我们可以注意到，稀疏率都很高（53.29% ∼ 93.43%），这意味着有很大的加速潜力。

输入补丁的高相似度
如第 2.1 节所述，Conv-ReLU 运算可以看作是固定的 Conv 权重向量和不同位置的许多输入补丁之间的许多向量乘法的组合。在典型的视觉推理过程中，Conv-ReLU 结构的输入补丁可能彼此相似甚至相同。

如图 3 所示，输入补丁之间的相似性可以在单个图像、不同图像和中间特征图中轻松找到。

2.3 机会和挑战

Conv-ReLU 结构中输出的高稀疏性和输入补丁之间的高相似性为我们带来了实现无损加速的机会。

具体来说，如果我们能够在不计算的情况下识别 Conv-ReLU 中的负输出向量乘法，我们就有机会通过跳过不必要的乘法来实现无损加速。
假设函数$\phi$计算向量乘法$\textbf{x}_{i,j}\cdot \textbf{w}_{k}$的上限值。

\[\overline{\textbf{y}_{i,j,k}}=\phi(\textbf{x}_{i,j},\textbf{w}_{k})=upperbound(\textbf{x}_{i,j}\cdot \textbf{w}_{k}) \]

函数$\phi$的具体计算流程如下:

\[\mathbf{y}_{i, j, k}=\left\{\begin{array}{lr} 0, & \text { if } \overline{\mathbf{y}_{i, j, k}} \leq 0 \\ \operatorname{ReLU}\left(\mathbf{x}_{i, j} \cdot \mathbf{w}_k\right), & \text { otherwise. } \end{array}\right. \]

意味着如果函数$\phi$的计算比向量乘法很轻量而且 0 值输出很多，那么 Conv-ReLU 的结构的计算量可以减少。
Wakatsuki 等人[46]提出了一种上限计算函数，可用于连续视频推理场景。具体来说，他们使用连续视频帧之间的输入补丁差来计算上限：

\[\begin{aligned} \mathbf{x}_{i, j} \cdot \mathbf{w}_k & =\mathrm{x}_{i, j}^{t-1} \cdot \mathbf{w}_k+\left(\mathrm{x}_{i, j}-\mathrm{x}_{i, j}^{t-1}\right) \cdot \mathbf{w}_k \\ & \leq \mathrm{x}_{i, j}^{t-1} \cdot \mathrm{w}_k+\left\|\mathrm{x}_{i, j}-\mathrm{x}_{i, j}^{t-1}\right\| \times\left\|\mathrm{w}_k\right\|, \end{aligned} \]

$\mathrm{x}_{i, j}^{t-1}$是上一帧中$\mathbf{x}_{i, j}$相同位置的补丁。这个公式计算上限是轻量级的，因为$\mathrm{x}_{i, j}^{t-1} \cdot \mathrm{w}_k$在上一帧中计算过了。$\left\|\mathrm{w}_k\right\|$ 是一个常量，$\left\|\mathrm{x}_{i, j}-\mathrm{x}_{i, j}^{t-1}\right\|$可以在计算不同卷积核的时候重用。但是，他们的方法只能应用于视频流，并且要求视频内容相对静态。如果帧间差异很大，推理成本甚至可能增加。

在一般的视觉推理任务中，使用上一帧进行对比是不可行的，但 Conv-ReLU 输入补丁之间的相似性为我们带来了另一个机会——我们可以让一些输入补丁作为同一前向传递中其他类似输入补丁的参考。然而，用它来实现无损加速并非易事，必须解决三个困难：

如何在单个推理过程中选择参考补丁。参考必须有用，并且选择必须有效以实现加速。
如何根据所选引用有效地检测和跳过不必要的计算。
如何保持 Conv-ReLU 操作的并行性，使加速方法能够兼容移动 SIMD 架构。

3 CONVRELU++

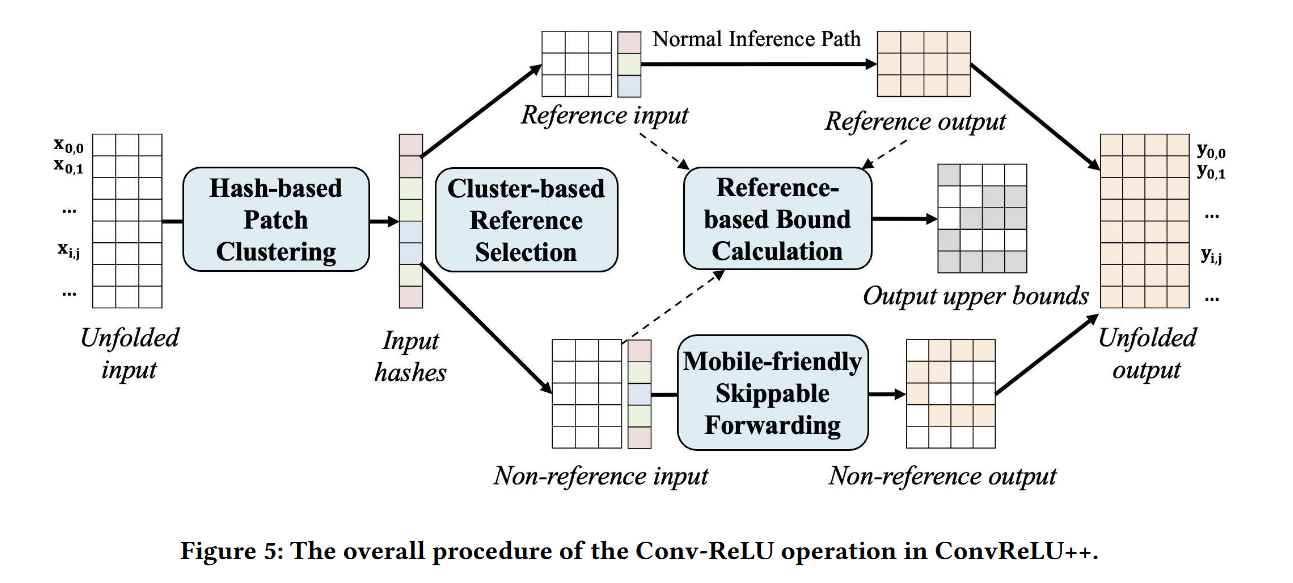
首先，我们引入了一种补丁哈希方法，将相似的输入补丁聚类到组中。通过使用轻量级哈希函数 $\textbf{patch\_hash}$（第 1 行）直接计算所有输入补丁的$cluster\_id$, 可以有效地实现聚类。

然后我们选择聚类质心作为参考补丁，剩下的补丁表示非参考补丁。参考的 Conv 输出（即参考 Patch 和 Conv 内核之间的点积）是在其他输入 Patch 之前预先计算的。

接下来，对于每个非参考输入补丁 $\mathbf{x}_{i,j}$ 和卷积核$\mathbf{w}_{k}$。ConvReLU++计算他们点积的上限，上限的计算依赖于参考输入补丁$\mathbf{x}_{i,j}^{ref}$和它的预计算点积结果$\mathbf{y}_{i,j}^{ref}$。参考输入补丁$\mathbf{x}_{i,j}^{ref}$用来和其他的同组的$\mathbf{x}_{i,j}$比较相似度。

最后每次实际计算$\mathbf{x}_{i,j} \cdot \mathbf{w}_{k}$时，ConvReLU++通过计算上限$\overline{\mathbf{y}_{i,j,k}}$来决定是否跳过长向量计算。

Conv-ReLU 运算$\mathbf{y}$的最终输出是参考输出、跳过的向量乘法产生的零点以及不可跳过的向量乘法的结果的组合。

3.1 基于 Hash 的参考选择

在 ConvReLU++ 算子内核中，第一步是选择一组参考输入补丁，稍后将与其他输入补丁进行比较，以便进行不必要的操作检测。

参考选择应满足几个目标。首先，参考补丁应代表所有输入补丁，以确保它们在以后的比较中是有效的。其次，选择必须高效，开销远小于相应的 Conv-ReLU 计算。第三，所选参考的数量应该是可控的，因为过多的参考会带来很大的开销，而参考太少可能会降低效果。直观地说，从大量输入补丁中查找代表性推论的一种方法是聚类。可以将相似的补丁组合在一起，并可以选择聚类质心作为参考。然而，将传统的聚类方法（如 k-means[17]）应用于参考选择是不可行的，因为它需要在输入补丁之间进行密集的比较，这在运行时太耗时了。

相反，我们尝试通过哈希将输入补丁直接划分为组。具体来说，我们设计了一个哈希函数 patch_hash，将每个输入补丁映射到一个哈希 ID，具有相同哈希 ID 的输入补丁属于同一个集群。我们的方法类似于局部敏感哈希（LSH），但我们的方法效率更高，因为我们的哈希函数通过一步直接生成集群 ID，而不是在传统的 LSH 中计算和转换多个位。我们观察到卷积核能够提取输入特征，其中相似的输入补丁具有相似的输出值。为了使哈希函数高效，我们将平均卷积核的输出值转换为整数作为哈希索引。簇质心的选择并不是那么重要，为了简单起见，我们选择第一个作为质心。详细设计介绍如下。

首先，由于 Conv-ReLU 内核中使用了哈希函数，因此我们建议直接使用轻量级的 Conv 层作为哈希函数。假设原始 Conv 内核的形状为$ R \times S \times C \times K$，其中 $R \times S$ 是内核大小，C 和 K 是输入和输出通道大小。哈希函数的 Conv 核形状设置为 $R \times S \times C \times 1$，以便哈希函数可以预测 x 中每个输入补丁的一个值。

哈希函数的效果相当于对每个输入补丁执行线性变换:

\[patch\_hash(\mathbf{x}_{i,j})=w^{hash} \cdot \mathbf{x}_{i,j} \]

$w^{hash}$ 是和卷积核$\mathbf{w}_{k}$一样长的向量。$w^{hash}$的权重设置为当前 Conv-ReLU 结构中所有 Conv 滤波器的平均值，以便 patch_hash 值之间的距离可以反映输入补丁之间及其相应输出值之间的相似性。

patch_hash 的输出是一个浮点数(显然是 0-1 之间)。我们通过缩放和舍入将其进一步转换为集群 ID：

\[cluster\_id=round(\lambda \times patch\_hash(\mathbf{x_{i,j}})) \]

这里 $\lambda$ 是用于控制簇大小的超参数。通过此转换，相似的输入修补程序将具有相同的$cluster\_id$。

最后，我们选择每个集群中的第一个输入补丁作为集群质心，该质心用作同一集群中其他补丁的参考补丁。我们保存输入补丁和$cluster\_id$ 之间的映射，以及$cluster\_id$和集群质心之间的映射，以便可以有效地检索每个输入补丁的参考，复杂度为$O(1)$。同时，哈希值的计算只需要 1/C 计算，其中 C 是 Conv-ReLU 的输出通道大小。因此，我们的设计实现了参考选择的有效性和效率的目标。

3.2 基于参考的上限计算（重点）

我们系统中有界计算的目标是预测输入补丁和 Conv 滤波器之间的点积是否为负，以便在不牺牲精度的情况下跳过乘法。
我们的上限计算基于:

\[\mathbf{y}_{i,j,k} = \mathbf{x}_{i,j} \cdot \mathbf{w}_{k} \leq \mathbf{y}_{i,j,k}^{ref} + \phi(\mathbf{x}_{i,j}-\mathbf{x}_{i,j}^{ref} , \mathbf{w}_{k}) \]

为了方便描述$\mathbf{x}_{i,j}-\mathbf{x}_{i,j}^{ref}$表述为$\delta$。

具体的计算函数上限函数:

\[\phi(\delta,\mathbf{w}_{k})=\delta[I_{diff-sub}] \cdot \mathbf{w}_{k}[I_{diff-sub}] + \Vert{\delta}\Vert \times \Vert{\mathbf{w}_{k}[I_{diff-sub}^{c}]}\Vert \]

$I_{diff-sub}$是一个向量索引的小子集，$I_{diff-sub}^{c}$是它的补集。$\delta[I_{diff-sub}]$,$\mathbf{w}_{k}[I_{diff-sub}]$ 和 $\Vert{\mathbf{w}_{k}[I_{diff-sub}^{c}]}\Vert$是$\delta$和$\mathbf{w}_{k}$的子向量。

接下来详细介绍相关细节。
首先，通过比较$\delta$和$\mathbf{w}_{k}$中元素的符号，我们可以得到向量索引$I_{all}$的两个子集。$I_{same}$是元素具有相同符号的索引，$I_{diff}$是符号不同的索引。

\[I_{same}=\{i | \delta[i] \times \mathbf{w}_{k}[i] > 0\} \\ I_{diff}=\{i | \delta[i] \times \mathbf{w}_{k}[i] \leq 0\} \]

然后点积$\delta \cdot \mathbf{w}_{k}$可以分为两部分，包括正部分（两个同号子向量的点积）和非正部分（两个不同符号子向量的点积）,因此可以写成:

\[\delta \cdot \mathbf{w}_{k} = \delta[I_{same}] \cdot \mathbf{w}_{k}[I_{same}] + \delta[I_{diff}] \cdot \mathbf{w}_{k}[I_{diff}] \leq \\ \Vert{\delta[I_{same}]}\Vert \times \Vert{\mathbf{w}_{k}[I_{same}]}\Vert + \delta[I_{diff}] \cdot \mathbf{w}_{k}[I_{diff}] \]

比较每一个$\delta$和$\mathbf{w}_k$的元素的符号是非常耗时的，在实际操作中，我们仅仅比较$\mathbf{w}_k$中很少一部分数量（E=6）的最大的幅值元素。假设$I_{diff-sub} \subseteq I_{diff}$是较$\mathbf{w}_{k}$中前 E 个最大幅值元素和$\delta$不同符号的索引。那么$I_{diff-sub}^{c}=I_{all}-I_{diff-sub}$就是其他索引。那么我们可以计算得到

\[\begin{aligned} & \delta \cdot \mathrm{w}_k \leq\left\|\delta\left[I_{\text {diff-sub }}^c\right]\right\| \times\left\|\mathrm{w}_k\left[I_{\text {diff-sub }}^c\right]\right\| \\ & +\delta\left[I_{\text {diff-sub }}\right] \cdot \mathbf{w}_k\left[I_{\text {diff-sub }}\right] . \\ & \end{aligned} \]

因为$I_{diff-sub}^{c}$是一个很长的索引列表，计算它对应的元素的幅值是非常重的。我们可以离线地预先计算$\left\|\mathbf{w}_k\left[I_{\text {diff-sub }}^c\right]\right\|$通过不同的$I_{diff-sub}$的组合。除此之外，我们可以用$\left\|{\delta}\right\|$替换掉$\left\|{\delta[I_{diff-sub}^c]}\right\|$。这样公式可以继续改写成：

\[\begin{aligned} \delta \cdot \mathbf{w}_k & \leq\|\delta\| \times\left\|\mathbf{w}_k\left[I_{\text {diff-sub }}^c\right]\right\|+\delta\left[I_{\text {diff-sub }}\right] \cdot \mathbf{w}_k\left[I_{\text {diff-sub }}\right] \\ & =\phi\left(\delta, \mathbf{w}_k\right) . \end{aligned} \]

而基本上限公式可以写成

\[\phi_{\text {base }}\left(\delta, \mathbf{w}_k\right)=\|\delta\| \times\left\|\mathbf{w}_k\right\| \]

很显然,$\phi(\delta,\mathbf{w}_k)$
比$\phi_{base}$更加紧凑（上限更小），因为$\|\delta\| \times\left\|\mathbf{w}_k\left[I_{\text {diff-sub }}^c\right]\right\|<\|\delta\| \times\left\|\mathbf{w}_k\right\|$而且$\delta\left[I_{\text {diff-sub }}\right]$和$\mathbf{w}_k\left[I_{\text {diff-sub }}\right]$都是负数。

综上所述，这样我们得到的$\phi\left(\delta, \mathbf{w}_k\right)$是一个只要对少量索引( $I_{diff-sub}$ )进行符号比较，计算两个短向量的点积($\delta\left[I_{\text {diff-sub }}\right] \cdot \mathbf{w}_k\left[I_{\text {diff-sub }}\right]$),向量的幅值$\|\delta\|$被计算完后可以被所有卷积核共享。

4 实验评估

4.1 计算量

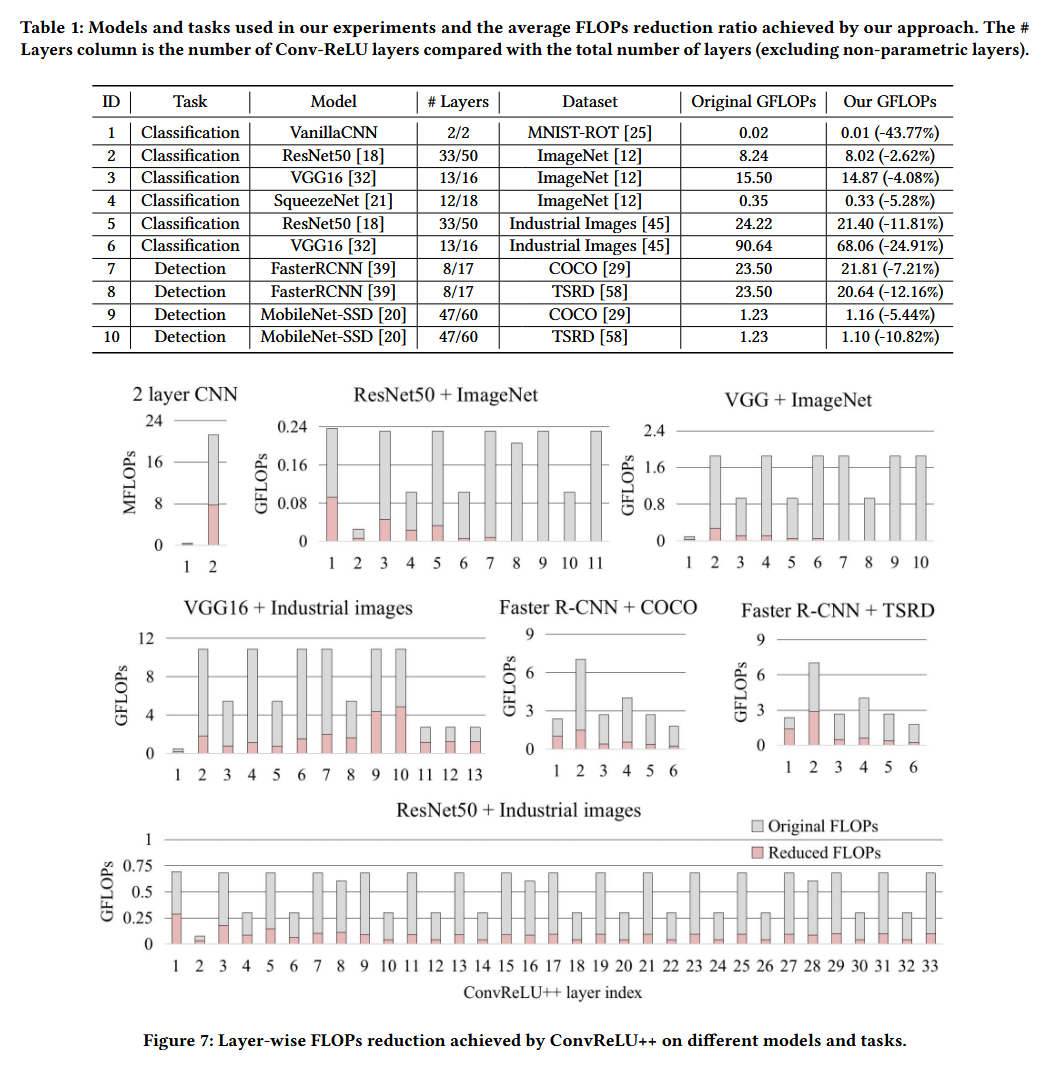
首先，ConvReLU++实现了所有任务的无损 FLOPS 降低，根据结果，降低率在 1.87%-43.77%之间。鉴于我们的方法是一种无损方法，我们相信我们的方法可用于广泛的深度视觉任务。我们方法的计算约简率高度依赖于数据集和模型。

数据集的影响。使用 MNIST-ROT 数据集的图像分类任务实现了最高的 FLOPS 减少（43.77%）。工业图像和 TSRD 数据集也产生了 24.91%和 12.16%的高 FLOPS 缩减率。然而，在 ImageNet 上，FLOP 的减少不太显著（低于 6%）。ConvReLU++表现良好的数据集的一个相似之处是图像包含大面积的相似像素（例如，背景、物体表面等），这有助于我们的方法选择更好的引用并跳过更多的向量乘法。许多其他真实世界数据具有与 MNIST 图像相似的属性，例如医学图像和空间图像。

模型架构对 ConvReLU++有效性的影响。在 ImageNet 数据集上，ResNet50、VGG16 和 SqueezeNet 实现了 2.62% 到 5.28% 的不同 FLOP 减少率。在工业图像数据集上，ResNet50 实现了 11.81% 的 FLOP 减少，VGG16 实现了 24.91% 的 FLOP 降低。我们的方法在 VGG16 上的表现一直比 ResNet50 更好。原因之一是 VGG16 包含了更大一部分的 Conv-ReLU 结构，我们的方法可以应用这些结构。此外，ResNet50 模型较深，且特征混合在一起时，深层空间局部性较低，降低了该方法检测可跳过向量乘法的能力。视觉任务的类型不会对我们的方法构成独特的挑战。我们在目标检测任务上观察到的 FLOP 减少模式与分类任务上的模式相似。

然而，由于检测模型中 Conv-ReLU 结构的比率较低，因此加速率不如分类任务高。我们进一步对每个 Conv-ReLU 层中的 FLOPS 减少进行了细分分析。结果如图 7 所示，我们可以观察到几乎所有的 Conv-ReLU 层都可以从我们的 FLOP 减少方法中受益。然而，在较深的层中，FLOPs 的减少率通常较低，这解释了我们的方法在较浅的网络上表现更好的原因。

4.2 有效性分析

参考帧选择,我们将基于哈希的参考选择方法与两个基线进行比较，

使用一个步长选择策略，（将$\mathbf{x}_{i,j}$作为{ $\mathbf{x}\_{i,j-k}$ 到 $\mathbf{x}\_{i,j+k}$}的参考补丁）
使用随机选择策略。

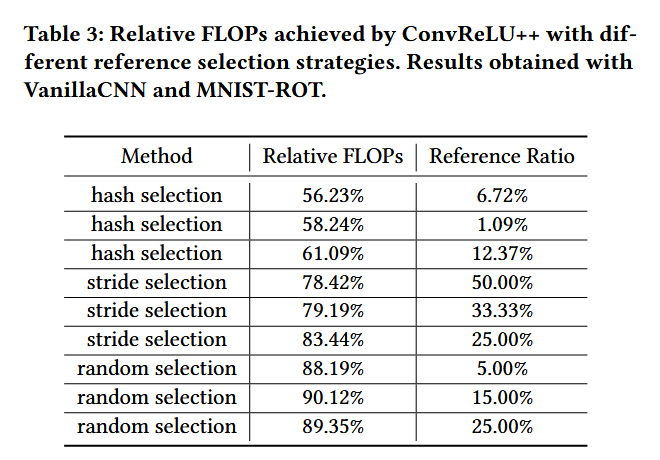
表 3 展示了 ConvReLU++使用 3 种选择策略后的 FLOPs 影响。最佳参考有效性（56.23% 相对 FLOP，即 43.77% 的 FLOPs 减少）是通过我们基于哈希的策略实现的，参考比率为 6.72%。这是由于我们的方法能够通过有效的散列来聚类相似的补丁。随机参考选择策略是无效的，因为它只能在不同的参考比率下产生 10%的 FLOP 减少。步幅策略更好，因为它利用了一些简单的空间局部模式，尽管效果仍然比我们的低得多。

上限计算的有效性。$\phi$ 是我们方法中的关键组成部分（公式 5），我们通过检查它是否产生比正常上限 $\phi_{base}$ 更紧密的边界（公式 7）来单独评估它。如图 9 所示，ResNet50 中所有卷积操作中 $\phi_{base}$ 的平均值为 0.95，最小值为 0.17。基于分布，我们的方法在大多数情况下比 $\phi_{base}$ 更紧密的边界，因此可以跳过更多的向量乘法运算。图 9 的右侧比较了使用 ConvReLU++ 与不同边界估计方法获得的端到端 FLOP 减少。

4.3 延迟

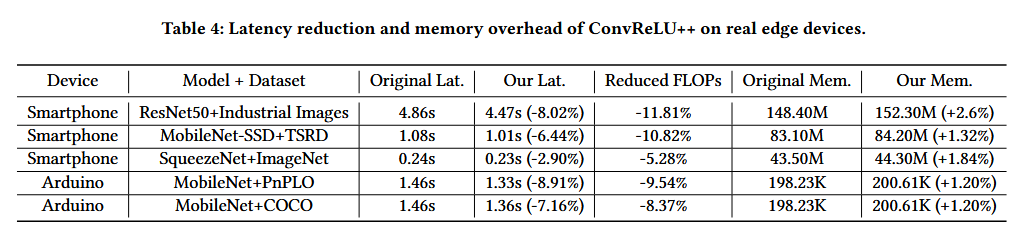
我们进一步研究了 ConvReLU++ 的 FLOP 减少是否可以映射到实际边缘设备上的实际延迟减少。具体来说，我们在两个具有代表性的设备上测试了五个推理任务，包括 Android 智能手机和 Arduino Nano 板。

如表 4 所示，使用 ConvReLU++ 可以降低智能手机和 Arduino 板的延迟，从而证明了 ConvReLU++ 在实际边缘设备上的适用性。然而，我们也观察到延迟减少小于 FLOP 减少（即延迟减少的理论上限）。这有几个原因：

在 Conv-ReLU 操作期间预计算和检索参考输入和输出可能会破坏内存访问的顺序模式，从而导致更高的缓存未命中率并减慢计算速度。
推理框架在智能手机上以多线程并行方式运行，ConvReLU++中的可跳过向量乘法无法充分利用密集矩阵乘法的并行性。
Arduino Nano 上使用的模型是 int8 量化的，但我们 ConvReLU++ 内核中的哈希函数是基于浮点版本模型的。

上述一些问题可以通过工程工作来缓解，我们将其留到未来的工作中。尽管如此，延迟降低与 FLOP 降低处于相似的水平，这表明 ConvReLU++ 与移动平台兼容。

posted @ 2024-01-03 23:23 SheepHuan 阅读(75) 评论(0) 编辑收藏举报

刷新页面返回顶部

SheepHuan的博客