贝叶斯网络——D分离的介绍
D分离——贝叶斯网络
文章结尾有例题分析。
基本概念
D分离的概念来自于贝叶斯网络,是用来寻找条件独立的有效方法
条件独立性:有节点A,B,C,如果有
\(P(A|B,C)=P(A|B)\)
即给定B(或者说B已确定)时,C的任何信息都不能改变A的可信度度量,则称A和C是在B的条件下独立的.
条件独立性有什么用呢?
答案是帮助我们简化贝叶斯网络的联合概率的计算
有向网络连接中节点间的三个基本关系
由于贝叶斯网络是一个DAG(有向无环图)网络。所以节点间的关系基本分为三类。
(1) 串行连接
在串行连接中A通过事件B影响C,同样事件C也是用过事件B影响A。我们认为当证据B确定时,A、C条件独立。
称A和C被B节点D分离。
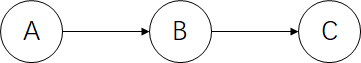
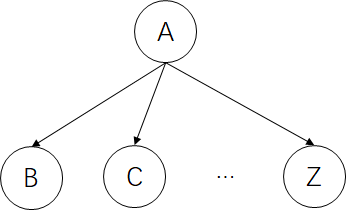
(2) 分叉连接
在分叉连接中A影响子节点,同样子节点通过A影响其他子节点。我们认为当A已知时,其各个子节点相互独立。称B、C、...、Z被A节点D分离。
(3) 汇集连接(比较特殊)
在汇集连接中只有A节点未知时,我们才能认为其父节点们相互独立。
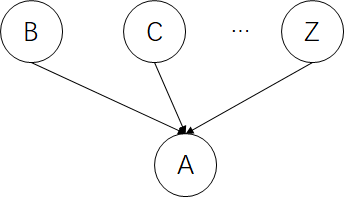
值得需要注意的是,如果某节点影响了节点A或者节点A的后代节点,我们认为其父节点们并不相互独立。
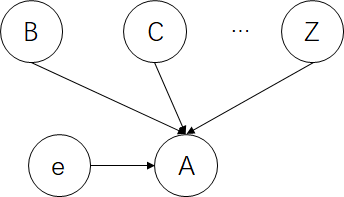
如上图,事件e直接影响了A,那么B、C...、Z并不独立
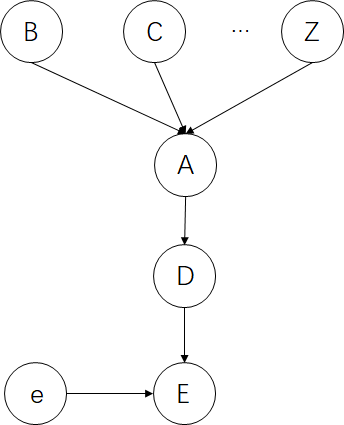
如上图,事件e直接影响了A的后代结点E,那么B、C...、Z并不独立。
D分离的条件
下面给出D分离的严格数学定义。
给定证据结点集𝛆,若对贝叶斯网络中\(V_{i}, V_{j}\)结点 之间的每一个无向路径都有某个结点\(V_{b}\)。若\(V_{b}\)存在以下三个属性之一,那么该无向路径被\(V_{b}\)阻塞。
- \(V_{b}\)在𝛆中,且路径上的两条弧都以\(V_{b}\)结尾。 (\(V_{b}\)相当于分叉连接中的A节点)
- \(V_{b}\)在𝛆中,且路径上的一条弧以\(V_{b}\)为头,一条弧以\(V_{b}\)结尾。 (\(V_{b}\)相当于串行连接中的B节点)
- \(V_{b}\)及其后代结点都不在𝛆中,且路径上的两条弧都以\(V_{b}\)为头。(\(V_{b}\)相当于汇集连接中的A节点)
若贝叶斯网络中\(V_{i}, V_{j}\)结点 之间的每一个无向路径都被阻塞,那么我们称\(V_{i}, V_{j}\)结点被证据集𝛆 D分离。
实例分析
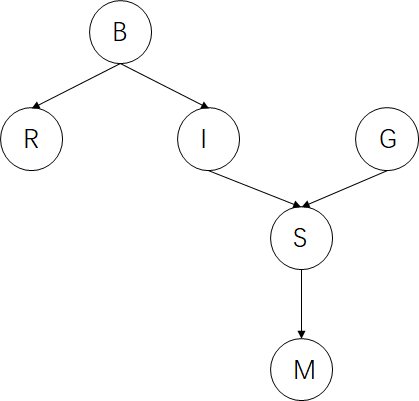
例1:如上图,利用D分离简化联合概率密度计算。
利用条件独立性简化计算前:
\(P(B,R,I,G,S,M)=P(M|B,R,I,G,S)*P(S|B,R,I,G)*P(G|B,R,I)*P(I|B,R)*P(R|B)*P(B)\)
利用条件独立性简化计算后:
\(P(B,R,I,G,S,M)=P(M|S)*P(S|I,G)*P(G)*P(I|B)*P(R|B)*P(B)\)
下面逐一分析:
\(P(M|B,R,I,G,S)\),可以被这样解决,给定节点B,R,I,G,S(可视为证据结点),判断它与那些节点条件独立,然后按照条件独立性化简。
- M,S直接连接,必然有影响,不独立。
- 给定S后,B,R,I,G.到M的所有无向路径被S阻塞。按照条件独立性\(P(M|B,R,I,G,S)=P(M|S)\)
\(P(S|B,R,I,G)\),同理。
- I,G和S直连,必然相互影响,不独立。
- 给定I后,B,R到S的所有无向路径被I阻塞。B,R和I条件独立,按照条件独立性\(P(S|B,R,I,G)=P(S|I,G)\)
\(P(G|B,R,I)\),同理
- B,R,I中没有结点阻塞G到B,R,I的所有无向路径。因为S没有给出且S的后代结点没有被给出结点B,R,I影响。所以B,R,I和G条件独立。\(P(G|B,R,I)=P(G)\)
\(P(I|B,R)\),同理
- 给定B后,RBI路径被B阻塞,所以R,I在B的条件下独立。\(P(I|B,R)=P(I|B)\)
例2:如下图,有三问
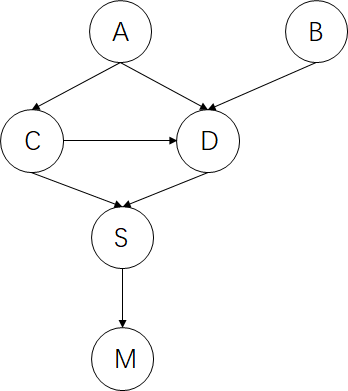
a) 列出从B到S所有无向路径
b) 给定证据结点D,那么a)中哪些无向路径被阻塞?
c) 等式\(P(S|B,D)=P(S|D)\)是否成立,为什么?
答:
a) 从B到S利用深度优先搜索的思路找到所有无向路径。
BDS,BDCS,BDACS
b) BDS,被D阻塞(B,S串行连接被D阻塞);BDACS,未被阻塞(A,B汇集连接处D已知,路径未阻塞);BDCS,未被阻塞(C,B汇集连接处D已知,路径未阻塞);
c) 由b)可知,B,S之间所有无向路径并未都被阻塞,B,S并不条件独立,所以等式\(P(S|B,D)=P(S|D)\)不成立。


