文献翻译:Deep Recurrent Neural Networkfor Multi-target Filtering
用于多目标滤波的深度递归神经网络
Mehryar Emambakhsh, Alessandro Bay, Eduard Vazquez Cortexica Vision Systems
London, UK
摘要:
本文利用自适应学习框架解决了多目标滤波中固定运动和测量模型的问题。这是通过定义目标元组为随机有限集术语和利用循环神经网络的长期短期记忆结构来实现的。提出了一种与预测的小轨元组相兼容的数据关联算法,在分配目标出生、存活和死亡的基础上,实现了被遮挡目标的更新。该算法在一个常用的滤波仿真场景中进行了评估,取得了很好的结果。
关键词:
滤波,RNN,LSTM,随机有限集
介绍
多目标滤波包括自动排除输入数据序列的杂波(通常是无标记的)。它在时空数据去噪、目标检测与识别、跟踪以及数据、目标和跟踪级传感器融合等方面有着广泛的应用。它还经常被用于各种军事应用(目标识别)、自动化管道、自动驾驶车辆,以及机器人定位和占用网格测绘(使用光学,例如立体相机或激光雷达,或雷达传感器)。特别是对于跟踪问题,多目标跟踪算法的性能很大程度上依赖于其滤波步骤。一种鲁棒的滤波算法能够考虑遮挡、检测概率、目标产生和生成的可能性,并考虑杂波密度。精确的滤波算法可以提高所生成轨迹(tracklets)的寿命和目标的定位能力。基于滤波算法的目标状态估计可以通过考虑先验运动模型和测量模型来实现。在贝叶斯滤波框架中,下一个时间步长目标的位置,而测量模型用于将预测映射到测量空间进行校正(更新步长)。然而,由于目标运动的高度复杂性,使用固定模型可能不会得到令人满意的输出,反而会恶化滤波性能。
考虑到这一挑战,同时受RNN循环神经网络跟踪器和随机有限集(RFS)多目标滤波范式的启发,在本工作中,我们提出了一种新的算法,在学习运动模型的同时进行多目标滤波。为此,在目标元组集上定义了一种长期短期记忆(LSTM)体系结构,并使用传入的数据序列在线训练。预测步骤是通过训练好的LSTM网络生成目标的数据补丁(data patch)。这个LSTM网络(接下来将会使用新的更新状态进行训练)逐渐学习被检测目标的全局可转移运动模型。在获得测量值后,我们使用了一种新的数据关联算法,该算法与生成的tracklet元组相兼容,用于分配新目标的存活、死亡和诞生。每个目标更新后的补丁用于下一个时间步训练LSTM模型。为了评估我们的算法,我们设计了一个多目标仿真场景。在仿真过程中,通过增加杂波(假阳性率)强度来评估滤波的鲁棒性。这篇论文是第一批用循环神经网络处理多目标过滤任务的论文之一,显示出了显著的潜力,优于知名的多目标过滤方法。
本文的组织结构如下:首先,第2节对文献中的相关工作进行了说明,第3节对整个流程进行了简要说明。在第4节中解释了用于运动建模的循环神经网络的合并。第5节将解释Tracklet元组和数据关联。第6节专门介绍实验结果。我们在第7节对论文进行了总结,并给出了未来的工作方向。
1.1科学的贡献
该算法能够对具有非线性运动和非高斯误差模型的多目标进行滤波。与【15,4】不同的是,不执行预训练的运动建模,从输入的数据序列学习从状态到观测空间的映射。此外,与[10]不同的是,该算法是在线训练,不依赖于单独的训练阶段。由于预测的目标随着时间的推移在目标元组中串联(concatenated),因此可以保持较高的马尔可夫顺序,从而实现更长的目标状态记忆。与RFS多目标滤波算法[15,4,2]相比,所提算法的超参数数量明显减少。例如,[2]除了杂波分布、生存和检测概率外,还需要超参数来执行输出密度函数的修剪、合并和截断。据我们所知,这是第一批解决循环神经网络多目标过滤任务的论文之一,特别是不需要预训练网络。
相关工作
多目标滤波算法可以分为两大类:1)基于模型的多目标滤波算法和2)基于非模型的多目标滤波算法。基于模型的方法依赖于对目标行为的预训练模型。这可以基于外观(appearance)或运动(运动学)方程。利用这些模型对每个目标定义的状态向量进行预测。然后将预测映射到测量步进(measurement step)进行校正。非基于模型的方法,是那些不假定预定义的目标运动模型的方法。这方面的著名例子包括蒙特卡罗方法,以及在过去几年中出现的深度神经网络。随着最近计算能力的进步,基于神经网络的方法已经能够从大量的序列中学习。这为多目标滤波打开了一个新的窗口,因为这些方法能够模拟数据序列中的潜在信息,同时过滤其假阳性样本。下面的小节将进一步详细介绍这两种不同的过滤范例。
基于模型的方法:在多目标滤波的贝叶斯公式中,目标是估计(隐藏的)目标状态的步长,从一组之前的时间步长的观察,即,
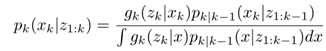 (1)
(1)
其中gk(zk|xk)和pk|k−1(xk|z1:k−1)分别为似然概率分布密度和跃迁概率分布密度。从(1)可以清楚地看出,这是一个递归问题。k次迭代时的状态估计通常采用最大后验概率(MAP)准则。
卡尔曼滤波可以说是最流行的在线滤波方法。它在预测和更新步骤中都采用高斯分布的线性运动模型。利用非高斯分布的泰勒级数展开和确定性逼近,分别用扩展卡尔曼滤波器(EKF [16],UKF[17])和Unscented卡尔曼滤波器(EKF [16],UKF[17])处理非线性和非高斯特性。利用重要抽样原理,利用粒子滤波器估计似然密度和后验密度。粒子滤波器是应用最广泛的针对非线性和非高斯运动的多目标滤波算法之一[18,3,19]。
Mahler提出了多目标滤波[11]的随机有限集(RFS)公式。RFS为多目标滤波提供了一种封装式,将杂波密度、检测概率、目标存活和诞生等因素综合在一起[2,3,11,12]。为此,目标和测量假设形成具有可变随机基数的集合。利用有限集统计量[11],(1)中的后验分布可以由向量扩展到RFS:

其中,Zk Xk测量值(包含杂波和真阳性)和目标RFS,µsan适当的参考测量值[13]。一种表示目标的方法是使用概率假设密度(PHD)图[3,13,2]。这些地图有两个基本特征:1)峰值对应目标位置;2)它们的积分给出了每个时间步的预期目标数。V o和Ma提出了高斯混合PHD (GM-PHD),将(2)中的一阶统计矩传播为混合高斯[13]来估计后验。
整体pipeline
整体管道框图如图1所示。首先,计算前一个时间步长的目标元组的预测位置。然后给出当前的测量值,为每个目标计算一组"残差"。然后用这些残差进行过滤(拒绝假阳性并获得存活)和分娩分配。最终将生成和存活元组集的并集作为迭代的目标。在下面的部分中将详细介绍这些步骤。
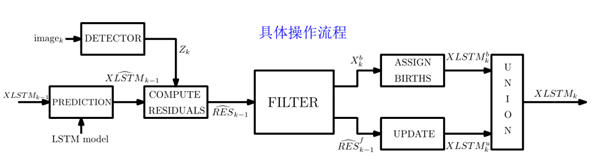
图1 本文提出的多目标滤波算法的总体流程是:将目标元组集XLSTMk−1赋给预测器,预测器为每个目标加载LSTM模型,在目标的最新数据补丁上进行训练,预测目标状态集ˆXLSTMk−1。由检测器得到测量集Zk,用于计算残差集。然后在残差集上执行过滤、数据关联和更新(修正)步骤,以消除数据中的杂波并分配生成,最终形成目标元组集XLSTMk。
基于LSTM的在线运动建模
目标状态在视频帧上的变化可以看作是一个序列学习问题。目标元组使用LSTM网络进行预测。用它们的相关测量更新后,每个目标的训练补丁被更新,这些目标被用来重新训练相同的LSTM模型。作为这种递归过程的结果,传入数据的运动建模被执行。使用这种方法学习到一个不结合任何先验知识的非线性/非高斯输入运动模型。在我们的工作中,我们研究了为每个目标分配一个LSTM网络,单独在之前的时间步长预测数据上训练以便预测接下来的目标位置。这种方法的主要问题是(GPU)内存管理及其可重用性。当目标数量增加时,释放与不在目标相关的(GPU)内存部分重新分配内存给新的目标是不可行的。
对此的一种解决方案是将单个LSTM网络定义为一个图,其节点只是"占位符"[31]指针变量。每次一个目标出现在场景中,占位符节点就被更新为与该目标对应的权重和偏差。一旦预测被执行,内存就被释放。这样的内存分配可以在视频序列中学习全局目标运动,这在人群行为检测中很有用,但在单独分析目标时结果较差。
因此,我们提出了一种在线LSTM训练的解决方案,其中每个目标与其他目标共享相同的LSTM权重(即A•,B•,b•,C, by )。在在线训练过程中,这些权重和偏差会从其他目标中共享,并根据过去的测量数据进行微调。换句话说,我们通过转移从另一个目标学习到的权值和偏差来微调每个目标的LSTM权值和偏差。这给了我们进一步节省记忆存储的优势,逐渐减少再训练时epochs的数量,并对每个特定目标有 主要受近期信息影响的 预测。在下面的部分中,我们将描述跟踪(tracking)管道,并展示如何将数据提供给LSTM网络以进行训练和预测步骤。
小段轨迹(tracklet)元组和数据关联
我们将一个tracklet元组xlstm定义为xlstm∈XLSTMk在时间k的子集,包含以下四个分量:
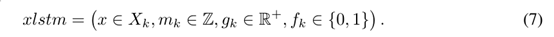
x是d维空间上的M×d目标状态矩阵。M为该目标之前追加预测的次数,作为LSTM网络的训练补丁。(M is the number of previous prediction appended for this target, which are used as the training patch for the LSTM network. )mkis是一个整数,表示目标到kthiteration为止的成熟度。Gkis是一个包含目标正数误差的实正数。Fkis是一个二进制冻结状态变量,当使用观察到的测量值更新目标的状态时,它为1;当更新没有使用任何测量值但使用目标的过去状态时,它为0。XLST Mkand Xkare具有Mkcardinalities的随机有限集,包含k处的所有目标元组,即xlstm∈XLST Mkand x∈Xk。
5.1过滤和出生分配
第 4 节中解释的 LSTM 架构用于预测目标状态 xk|k-1。这是通过首先使用来自 xlstm 元组的 M 个样本顺序训练 LSTM 网络来实现的。然后将 x 的最后(第 M)行中的样本提供给训练网络以预测 ^x,然后将其附加到输入元组 xlstm 以创建预测的元组 xlstmˆ ∈ XLSTMk|k−1。因此,得到的 XLSTMk|k-1 是一个具有 Mk-1 基数的 RFS,类似于 XLSTMk-1。在第 k 个时间步长,使用获得的测量值 RFS Zk 计算一组残差。如果 Zk 具有 Nk 基数,假设没有进行门控,将有 Nk × Mk−1 个残差存储为 RESk|k−1,其中 resˆ ∈ RESk|k−1 具有以下结构,
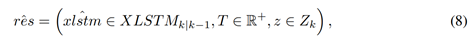
其中 T 是目标误差参数,由 T = kxˆ − zk2 计算得出。 T 的值显示预测目标与当前测量值的接近程度。 RESk|k-1 用于执行过滤步骤,在该步骤中确定目标的存活率、分配新生儿并去除假阳性目标和测量值。为此,首先构建一个 Nk ×Mk−1 目标矩阵 Tk|k−1,其在第 n k 行和第 m^ k 列的元素显示第 n k 个测量值和第 m^ 第 k 个预测目标之间的第二范数(nk = 1, 2, ... Nk 和 mˆ k = 1, 2, ... Mk−1)。在下一节中,我们将详细介绍如何使用 Tk|k−1 进行数据关联。
5.1.1 数据关联
对于 Tk|k−1 的每一列和每一行,测量指标和目标指标分别计算如下,
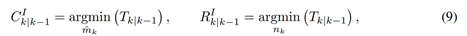
其中CI k|k-1 和RI k|k-1 是Nk × 1 和1 × Mk-1 向量,分别包含最小目标和测量指标。另外,还计算了Tk|k-1的每一列的最小值,
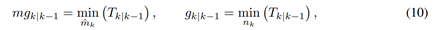
其中 mgk|k-1 和 gk|k-1 分别是包含测量和目标真实性误差的 Nk ×1 和 1×Mk-1 向量。换句话说,mgk|k−1(nk) 和 gk|k−1 (ˆmk) 分别是第 n k 次测量和第 mˆ k 次测量和目标的测量和目标真实性误差。在下一步中,C I k|k-1 和 RI k|k-1 的直方图 bin 分别计算为 HC I k|k-1 和 HR I k|k-1 ,如下所示,
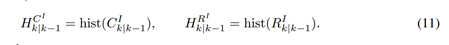
HC I k|kâˆ'1 (ˆmk) 的每个元素显示 mˆ k 预测目标存在多少关联。另一方面,HR I k|k∼'1 (nk) 的每个元素表示与第 n k 次测量的关联数。然后使用在算法 1 中解释为伪代码的数据关联方法更新目标的状态。
5.2更新存活并分配出生
存活的目标形成一个 RFS RESf k|k−1 。集合成员 resf ∈ RESf k|k−1 与 (8) 中的 resˆ 具有相同的结构,唯一不同的是它的 m、g、f 和 z 根据算法 1 中解释的情况进行更新。阶段(如图1的框图所示),如果目标的冻结状态为零,则意味着测量 zk 已成功与目标关联,则通过附加关联的测量 zk 来更新其 xk,即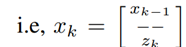 。另一方面,如果冻结状态为 1 ,意味着关联步骤未能找到当前目标的测量(可能是由于遮挡、测量失败或目标本身是误报),预测的目标状态 xˆk 被附加到 xk−1 以创建新的状态矩阵
。另一方面,如果冻结状态为 1 ,意味着关联步骤未能找到当前目标的测量(可能是由于遮挡、测量失败或目标本身是误报),预测的目标状态 xˆk 被附加到 xk−1 以创建新的状态矩阵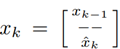 。
。

对于这两种情况,为了优化内存分配,我们定义了最大批量大小。如果 xk 中的行数大于批量大小,则将删除对应于最早保存的预测或测量值的 xk 的第一行。使用更新的目标状态,为幸存的目标生成一个 RFS XLSTMku 。它的每个成员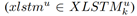 都是一个元组,具有与(7)相同的结构,根据数据关联计算更新状态。
都是一个元组,具有与(7)相同的结构,根据数据关联计算更新状态。
与上述过程并行,对于每个 1 × d 出生向量 xb ,一个目标元组被分配为
在第k个时间步的目标元组被计算为出生和存活的并集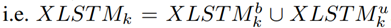
拥有Mk个基数(cardinality)

