Convolutional Recurrent Predictor: Implicit Representation for Multi-Target Filtering and Tracking
摘要:
定义多目标运动模型,是一个重要的跟踪算法的步骤。由于各种因素影响,从理论公式表达到计算复杂性,使得他是一项具有挑战性的任务。使用固定模型(如几种生成贝叶斯算法,如卡尔曼滤波器)可能无法准确预测复杂的目标运动。另一方面,序列性质的运动模型的学习(例如,使用循环神经网络)在计算上可能复杂且困难,因为目标的数量未知。在本文中,我们提出了一种多目标过滤和跟踪算法,该算法可以同时为所有目标学习运动模型。它通过隐式表示的状态图并执行时空数据预测来实现。为此, 在连续的假设目标空间上对多目标状态进行建模,使用随机有限集和高斯混 合概率假设密度公式(PHD)。使用具有长短期记忆架构的深度卷积递归神经网络递归执行预测步骤,该网络被训练为回归块,在运行中,概率密度差地图(PDD)。我们的方法在广泛使用的行人跟踪基准上进行了评估,显着优于最先进的多目标过滤算法,同时与其他跟踪方法相比提供了有竞争力的结果:所提出的方法分别在 MOT15 和 MOT16/17 数据集上生成平均 40.40 和 62.29 的最佳子模式的分配错误,同时,当使用公开可用的探测器,在 MOT16/17、PNNL 停车场和 PETS09 行人跟踪数据集上分别产生 62.0%、70.0% 和 66.9% 的多目标跟踪精度。
索引词—多目标过滤跟踪,随机有限 集合、卷积循环神经网络、长短期记忆、时空数据。
Index Terms—Multi-target filtering and tracking, random finite sets, convolutional recurrent neural networks, long-short term memory, spatio-temporal data.
卷积循环预测器:隐式多目标的表示过滤和跟踪
Mehryar Emambakhsh , Alessandro Bay, and Eduard Vazquez
2019年3月4日的文章
介绍
时空数据过滤在众多问题中,如安全、遥感、监视、自动化和天气预报算法中扮演关键角色。作为序贯滤波的任务(sequential filtering task)中很重要的一步,状态变量的预测(估计)提供了对过去、现在和未来数据的重要洞察。特别是对于多目标过滤和跟踪 (MTFT) 问题,预测步骤传达有关潜在状态变量的过去信息并建议目标提案(proposals)。 运动模型是贝叶斯过滤范式的基本组成部分,用于执行此任务。一旦建立了提案,就会通过状态到测量空间映射对它们应用更正(更新)步骤。卡尔曼滤波器假设线性运动模型具有高斯分布的预测和更新步骤。而非线性和非高斯行为分别由扩展和无迹卡尔曼滤波器(EKF、UKF) 解决,使用非高斯分布的泰勒级数展开和确定性近似。而使用重要性采样原理,粒子滤波器用于估计似然和后验密度,解决非线性和非高斯行为 [16]、[23]。Mahler 提出了随机有限集(RFS)[14],它提供了多目标过滤的封装公式,结合了杂波密度和检测、目标概率的生存和诞生。为此,假设目标和度量形成了具有随机基数的集合。表示目标状态的一种方法是使用概率假设密度 (PHD) 映射 [22]、[23]。Vo 和 Ma 提出了高斯混合 PHD(GM PHD),它传播一阶统计矩作为高斯混合 [22] 来估计后验。虽然 GMPHD 是基于高斯分布,但 Sequential Monte Carlo PHD (SMC PHD) 提出了一种基于粒子滤波器的解决方案来解决非高斯分布 [23]。由于在 SMCPHD 期间应传播大量粒子,因此计算复杂度可能很高,因此门控可能是非常必要的 [16]。Cardinalised PHD (CPHD)也被提议随着时间的推移传播RFS基数[13],而Nagappa等人解决了它的棘手问题[17]。标记多重伯努利滤波器(LMB)[19]具有航迹关联(执行轨道到轨道关联),在不依赖高信噪比(SNR)的意义上优于以往的算法。Vo等人提出广义LabelledMulti-Bernoulli (GLMB)作为标记多目标滤波[25]。
由于传入的数据通常是嘈杂的、杂乱的并且随时间变化,因此先验适用的运动模型并不总是能直接定义到所有目标。因此,贝叶斯滤波器所使用的目标状态到状态转换函数公式的这种不精确性将导致错误的预测。随着运动的复杂性增加,这种现象变得更加明显。因此,一个稳健的滤波算法应该能够学习这样的(多目标)运动行为,从而能够准确预测接下来的时间步骤。最近,机器学习见证了深度学习方法的兴起,在许多领域取得了最先进的结果,从通过卷积神经网络 (CNN) [11] 的图像分类任务到通过循环神经网络 (RNN) 的自然语言处理[8]。CNNs 可以通过在输入数据上滑动可学习滤波器来学习底层空间信息。另一方面, 作为非线性动态系统 [1],RNN 可以通过反馈循环存储和利用过去的信息。单元之间的循环连接允许 RNN 适用于预测时间序列,以这样 一种方式训练网络,使其当前(状态)输出用作以下步骤的输入。 引入长短期记忆(LSTM)架构 [10] 来解决 RNN 训练过程中梯度消失的现象。
虽然 RNN 和 CNN 网络能够分别从输入信号中学习时间和空间信息,但它们用于多目标数据分析并不简单。由于在 MTFT 问题中, 目标的数量在不断变化,因此使用具有固定架构的网络(神经网络通常具有固定和预定义的输入和输出神经元数量)无法轻松建模运动。一种解决方案是为每个目标分配一个 LSTM 网络 [4],这会显著增加计算复杂度。
在本文中,我们提出了一个解决上述两个问题的解决方案:(1) 通过贝叶斯过滤方法使用固定模型和(2)利用深度神经网络解决具有可变输入/输出大小(基数)的问题的困难,例如在 MTFT 中。我们将 MTFT 问题从显式离散多状态向量估计公式化为隐式多维时空预测。前者引入MTFT作为状态空间上的变量(未知)离散节点数,而后者则执行在连续状态空间上隐式的MTFT(类似于显式vs. 隐式的直觉存在与Snakes中vs. Level设置用于图像分割的活动轮廓[5],或者是K-means vs. 模式识别的层次聚类) 我们的方法基于定义概率密度差(PDD)图,它封装了状态空间上的多目标信息流。受到 Weinzaepfel 等提出的工作的启发,使用卷积网络进行密集光流计算 [26],然后,使用深度卷积 LSTM 网络(ConvLSTM [20])作为回归块,学习和估计时空预测:利用卷积滤波器对多目标状态空间上的空间依赖性进行建模,利用LSTM递归算法对时间依赖性进行学习。
正如题目所暗示的,我们提出的算法是概率图上的顺序预测器。然而,一个多目标并给出了输出预测图的卡尔曼更新步长,使本文具有完备性。
本文的组织如下。第二节介绍了 PDD 映射的概念,而整个 MTFT pipeline在第三节中有详细说明。实验结果在第四节中说明,我们在第五节中总结了论文。
关于数学符号:在整个论文中,我们使用斜体表示法来表示标量、RFS、概率密度函数(PDF)和PDD映射。我们用粗体表示向量、矩阵和元组。下标和上标分别表示 RFS 和标量/向量/矩阵的时间步长。
目标状态RFS集Xk 可以用来创造(假设)连续目标x的密度函数vk(x),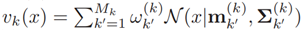 其中,
其中,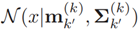 是依托于假设[22]的一个x标准描述。vk(x)可以得出在何处RFS集Xk到达最高处(峰值的位置)。而且混合高斯权重
是依托于假设[22]的一个x标准描述。vk(x)可以得出在何处RFS集Xk到达最高处(峰值的位置)。而且混合高斯权重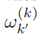 被设计成使得下述条件成立:
被设计成使得下述条件成立:
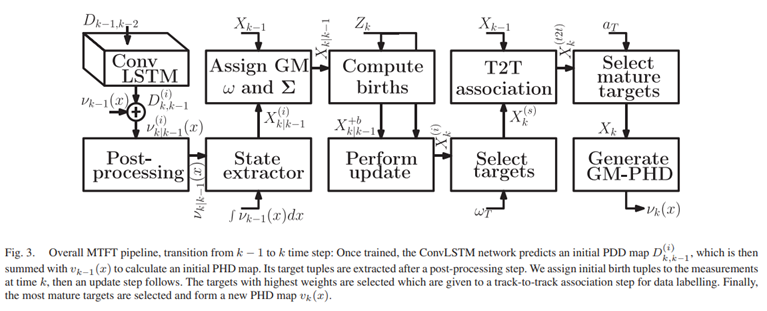
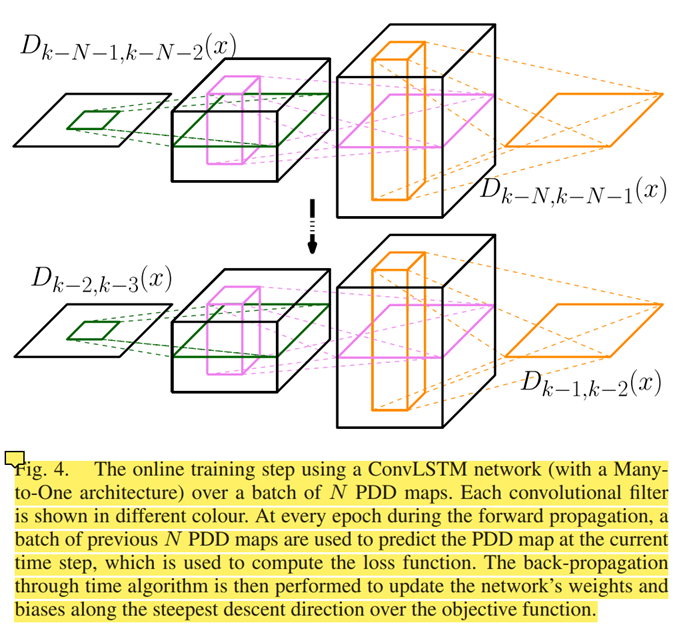
Dk-1,k-2(x) (图4中的输出) 输入给训练后的ConvLSTM网络计算初始预测PDD:D(i)k,k-1(x) (图3的输入)。当D(i)k,k-1(x)与PHD函数 vk-1(x)相加时后,返回(初始的)预测PHD map 
由于神经网络对输入数据施加的非线性和权重/偏差 乘法/加法运算,输出
V(i)k,k-1(x)
可能不满足 PHD 条件 (1)。此外,由于卷积滤波器使用的填充,可能会在输出数据的边界上添加伪影。为了解决这些问题,V(i)k,k-1(x)的边界值用内部中间部分的值代替。并且,我们假设预测步骤不会更改目标的数量。由于目标的数量等于PHD滤波器的集合,应用中值滤波之后,输出映射被归一化,使得它被集成到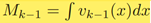 。这一步后处理的结果是PHD函数,然后用于提取预测的目标状态 RFS Xk|k-1。GM-PHD 函数中峰值的位置对应于目标状态的平均向量[22]。因此,为了从Vk,k-1(x)提取目标的显示状态,首先,他的峰值被建立成如下方程组:
。这一步后处理的结果是PHD函数,然后用于提取预测的目标状态 RFS Xk|k-1。GM-PHD 函数中峰值的位置对应于目标状态的平均向量[22]。因此,为了从Vk,k-1(x)提取目标的显示状态,首先,他的峰值被建立成如下方程组:
此时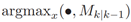 计算
计算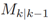 的最大峰值。
的最大峰值。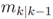 是一个具有如下基数的RFS集合:
是一个具有如下基数的RFS集合: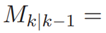
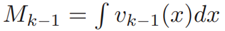 。包含预测的d维目标状态均值向量。Vk,k-1(x)的峰值对应的 GM-PHD 权重计算如下:
。包含预测的d维目标状态均值向量。Vk,k-1(x)的峰值对应的 GM-PHD 权重计算如下:
这里 Ωk|k1 是包含Mk|k1 目标的 GMPHD 峰的 RFS。为了计算RFS Σk|k1的协方差 , 我们研究了两种方法。第一种方法分别使用mk|k1 和Ωk|k1 作为混合高斯的位置和高度。然后将二维混合高斯函数拟合到PHD映射vk|k−1(x),以计算协方差矩阵。另外一个方法是基于使用组合优化找到均值RFS mk1和mk中对应的点(对)。然后Σk|k1赋值给Σk1中相应的元素。通过实验我们观察到,这两种方法得到了相似的结果,后者会快得多,因为它不是在连续参数空间上进行优化(与 2D 高斯拟合不同),并且不易停留在局部最小值处。上面解释的整体方法可以解释为来自隐式表示(vk|k−1(x))的映射(mapping)到一个明确的目标状态表示(Xk|k−1)。
Xk|k−1的集合和RFS 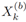 的出生,都是被指定使用现有的均值RFS Zk,他们采用下式进行计算:
的出生,都是被指定使用现有的均值RFS Zk,他们采用下式进行计算:
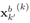 是kth步出生的目标元组,初始化协方差矩阵、出生权重、出生标签标识符,出生年龄和初始运动向量。预测的
是kth步出生的目标元组,初始化协方差矩阵、出生权重、出生标签标识符,出生年龄和初始运动向量。预测的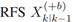 依据的RFS Zk量测更新。这将在下一章解释。
依据的RFS Zk量测更新。这将在下一章解释。
假设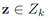 是d维的量测向量,更新过后的GM-PHD均值,协方差矩阵和高斯权重将采用以下计算方式:
是d维的量测向量,更新过后的GM-PHD均值,协方差矩阵和高斯权重将采用以下计算方式:
以下更新步骤之后,目标中权重高于设定的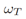 的被选中为初始的更新的目标
的被选中为初始的更新的目标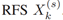 。使用目标
。使用目标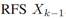 ,track-track 关联算法将在选中的目标中执行。
,track-track 关联算法将在选中的目标中执行。
距离度量是计算前一个时间步长的第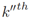 个目标
个目标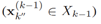 和
和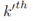 (当前未标记的)目标在当前时间步长处计算的:
(当前未标记的)目标在当前时间步长处计算的:
目标的死亡:另一方面,如果目标没有测量值关联,而且目标的年龄小于aT,则目标死亡。


 ,此时Mk代表目标的数目(集基数)。每个
,此时Mk代表目标的数目(集基数)。每个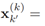
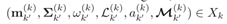 是k
是k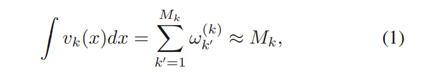
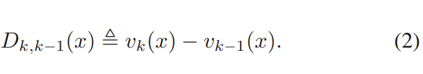
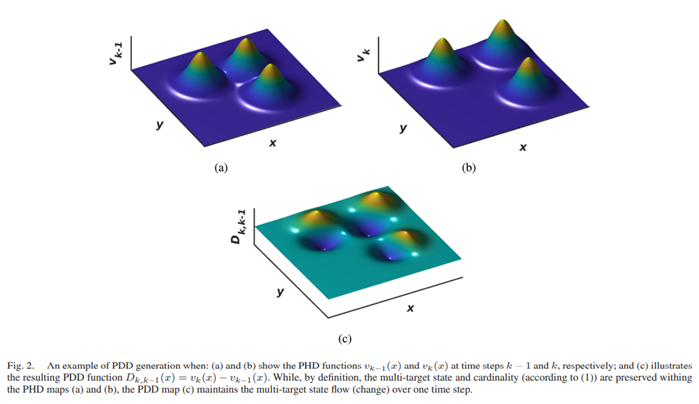
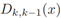 包含目标状态流动 两个连续时间步之间的信息,强调最近的变化。从两个连续的PHD图中创建PDD函数的过程如图2所示。图2-a和-b中的峰值位置分别对应于时间步长k和k-1时的目标状态(例如目标的运动学属性)。将这两个图相减,生成PDD图Dk,k-1(如图2-c所示),该图保留了一个时间步长内多目标状态的过渡信息。
包含目标状态流动 两个连续时间步之间的信息,强调最近的变化。从两个连续的PHD图中创建PDD函数的过程如图2所示。图2-a和-b中的峰值位置分别对应于时间步长k和k-1时的目标状态(例如目标的运动学属性)。将这两个图相减,生成PDD图Dk,k-1(如图2-c所示),该图保留了一个时间步长内多目标状态的过渡信息。
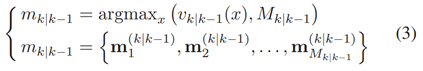
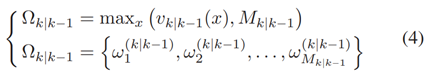
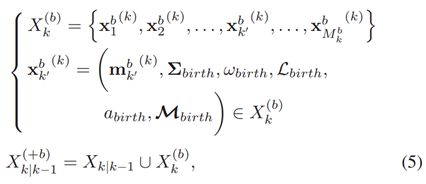
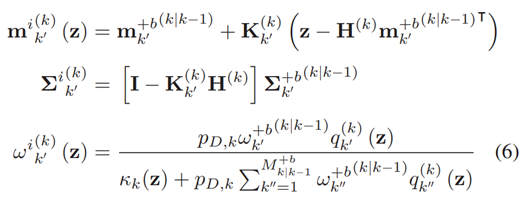


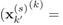
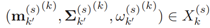 ,
,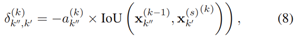
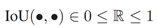 计算两个目标并集的交点。
计算两个目标并集的交点。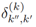 计算两个目标之间距离的估计,
计算两个目标之间距离的估计,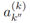 是目标在先前时间步的年龄,它和IoU相乘提升那些长期存在的目标的重要性。在所有之前和现在的目标中计算
是目标在先前时间步的年龄,它和IoU相乘提升那些长期存在的目标的重要性。在所有之前和现在的目标中计算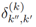 ,构成矩阵
,构成矩阵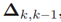 ,者会被给予Hungarian Assignment algorithm用来决定目标的生存、出生和死亡,就像算法1中的伪代码一样。
,者会被给予Hungarian Assignment algorithm用来决定目标的生存、出生和死亡,就像算法1中的伪代码一样。
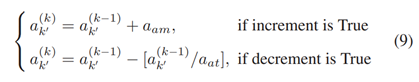
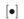 计算整数部分
计算整数部分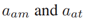 (都属于
(都属于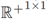 )分别是目标年龄的放大因子和衰减因子。最后,选取年龄大于阈值aT的最成熟目标作为Xk。Xk紧接着被用于计算PHD函数
)分别是目标年龄的放大因子和衰减因子。最后,选取年龄大于阈值aT的最成熟目标作为Xk。Xk紧接着被用于计算PHD函数
 浙公网安备 33010602011771号
浙公网安备 33010602011771号