《统计学习方法》 三要素和模型的选择
统计学习的三要素：
统计学习方法 = 模型 + 策略 + 算法
无监督学习
模型有以下三种表示方式：
Z来自于隐式结构空间的。
模型相应的假设空间分别是：所有可能的函数组成的集合，给定x的情况下z的条件概率分布集合 或者 给定z的情况下x的条件概率分布集合。
参数空间：所有可能的参数θ。
策略：优化目标函数
算法：通常是迭代算法
监督学习
模型
假设空间（Hypothesis Space）：所有可能的条件概率分布或者决策函数，用F表示。
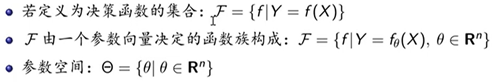
策略
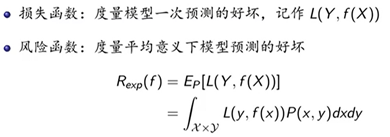
假设空间中的每一个模型F，都求一个风险函数，值最小的F就是最优模型。
但是，联合分布P(x,y)并不能求出，所以风险函数不能直接进行计算。此时我们选择一个经验值替代。
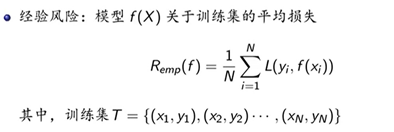
四种常见的损失函数：
当样本容量N足够大的时候，可以认为经验风险是风险函数的一个估计值：
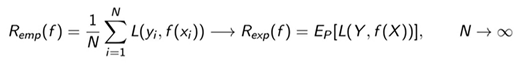
此时，只需要选取使经验风险最小的模型函数即可。
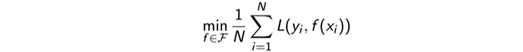
但是，当样本容量N比较小的时候，仅仅将经验风险最小化，可能会造成过拟合的情况。因此引入结构风险的概念，结构风险就是在经验风险的基础上加了一个惩罚项：
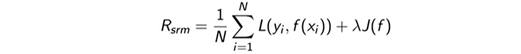
这个惩罚项J(f)是针对模型的复杂度的，模型越复杂结构风险越小。结构风险平衡了经验风险和模型的复杂度。结构风险最小化，就是选取使得结构风险最小的那个模型。
监督学习的策略就是选取一个目标函数（经验分享/结构风险），通过优化这个目标函数达到学习模型的目的。
算法
算法是用来求解最优模型的。若优化问题存在显示解，则算法较为简易。通常是不存在解析解的，需要数值计算的方法，比如梯度下降法。
当模型、策略、算法决定的时候，相应的统计学习的方法也就决定了。
训练误差与测试误差
定义：
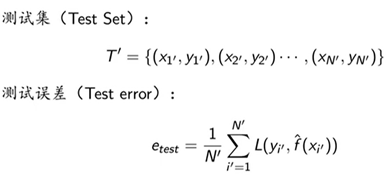
过拟合
过拟合（Over-Fitting）：学习所得模型包含参数过多，出现对已知数据预测很好，但对未知数据预测很差的现象。
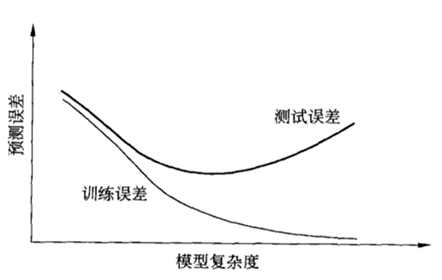
模型选择时，要尽可能选择训练误差和测试误差都较小的模型。
模型选择：正则化与交叉验证
正则化：使得结构风险最小化的策略。
- 一般形式：
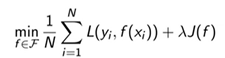
- 经验风险：
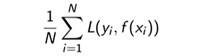
- 正则化项：（惩罚项）
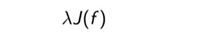
其中，J(f)代表模型的复杂度。模型参数越多，复杂度越高。
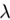越大，最后通过正则化选择的模型参数就会越少，模型越简单。
常见的正则化项
奥卡姆剃刀原理
内容：在模型选择时，选择所有可能模型中，能很好解释已知数据并且十分简单的模型。
交叉验证
数据充足的情况下，将数据集分为训练集、验证集和测试集。
数据不足的情况下，采用交叉验证的方法。
简单交叉验证：将数据集随机分为两个部分，训练集和测试集。
S折交叉验证：随机将数据分为S个互不相交、大小相同的子集，其中以S-1个子集作为训练集，余下的子集作为测试集。
留一交叉验证：S折交叉验证的特殊情形，取S=N。
