【课程笔记】神经网络训练细节part1

第12课 神经网络训练细节part1（下）

用高斯分布初始化相关参数，然后乘以权值0.01，称为高斯分布初始化。
本节中我们着重关注隐藏层中的神经元会如何激活，将均差和标准差绘制成柱状图。

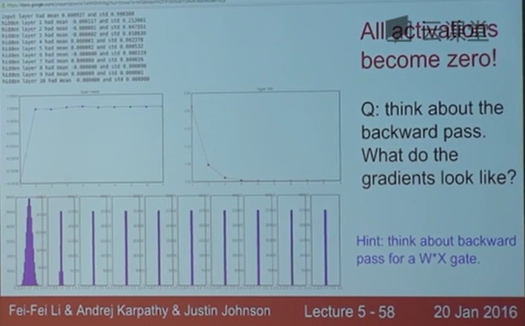
使用高斯分布的数据，让他们与w参数相乘，然后通过激活函数。最终所有的数据都将坍缩到0。而在我们反向传播时要求x的梯度，最终的梯度也会相当的小。这就是我们所说的梯度弥散。

如果使用这种方式初始化数据，我们会发现梯度的量级在不断缩小。

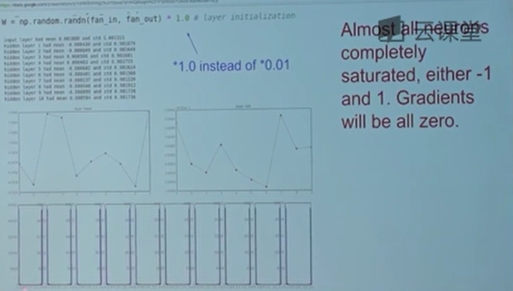
所以我们可以尝试另一种方法，尝试一些别的尺度来初始化W，用1.0来代替0.1。这时候经过实验会发生另一个奇特的事情，所有的数值都趋于饱和，激活函数的输出，不是-1就是1，这意味着网络中传递的数值都过于饱和了，权重设置的太高了。所有神经元都饱和之后是无法进行反向传播的。

针对这个问题，2010年Glorot的论文提出了Xavier初始化。但是这个方法只能在用tanh激活函数中奏效，在使用relu作激活函数时，它并不奏效，并且方差的下降会更快。这里讲解了一种当使用relu作为激活函数时的初始化方法。

总结来说初始化是非常重要的，如果初始化的方式有问题，就不会得到好的结果。

研究合理的初始化也是一个热门的领域，可以看到有很多这方面的论文。这些论文都很有意思，但是他们并没有一个标准的初始化公式。我们在运行程序的时候，希望我们得到一个高斯分布的方差，所以这个工程是一个数据化驱动的工程，并且有一定的准则。

接下来讲解一些技术细节。

批数据的规范化。

批数据的规范化一般在全连接层和激活函数层后。它会保证神经网络里的每一步的每一个东西都是roughly unit gaussian。

另一件事，BN实际上起到了一些正则化的作用，而且它减少了Dropout的需要。

照顾我们的训练过程。

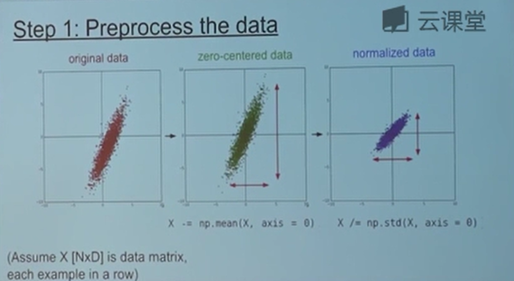
首先要预处理数据。

 

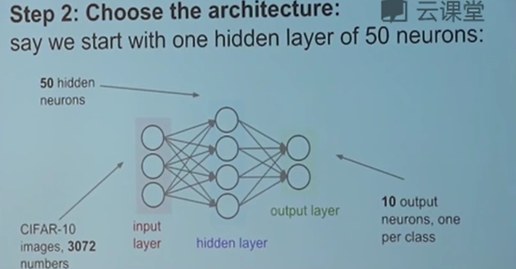
然后是选择一个合适的网络架构。

 

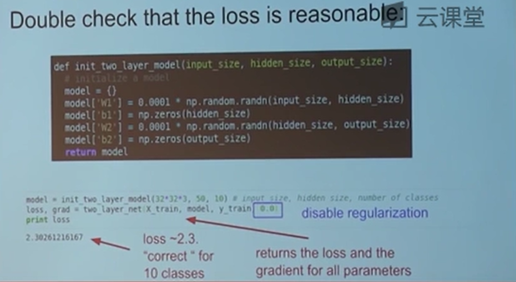
再次确认我们的loss函数是可行的。这时候我们在一个简单的2层神经网络中去判断我们的loss值是否是正确的。在一开始的时候只是一个非常简单的网络，然后逐步的增加正则化等相关过程，来确保loss的变化跟自己预想的一样，这样做的是一个非常好的完整性的检查。

接下来尝试小数据量的测试训练。比如使用20个数据和20个标签来保证我的模型，在基于这一小部分数据训练的时候，损失值基本为0。如果可以完全过饱和这部分数据，那么有些地方就一定会产生问题。当你在小批量数据上可以训练得到较好的损失值的时候，那么就可以充分相信自己的反向传播是在正常工作的，更新也应该是在正常工作的，学习率也设置的很合理。之后会考虑扩大数据训练规模。

（视频中提到的过饱和应该是常说的过拟合）

这里还提到了一个控制学习率的小技巧。学习率太小的话，损失函数会降的非常的慢，而学习率过大，比如说100万的时候损失函数会直接变成nan（发散，爆炸了）。

超参数优化。

这部分讲如何从粗糙到精细化去找到系统最好的超参数。我们现在一个大的范围内确定一个更小的范围，然后在相对小的范围中去选择出我们所需要的最优的值。这个过程可以用循环来实现，在每个循环中都进行取样超参数值，然后进行训练得到结果。另外有一个小的tips，当我们对正则化和学习率进行改变的时候，最好从对数空间中取样。

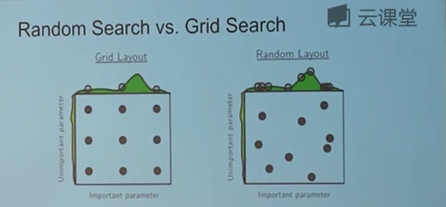
而且一般情况下使用随机取样，它能给我们更好的优化结果。一般优化的超参数有学习率，正则化还有差量。

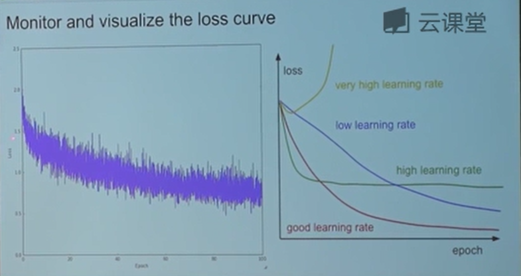
损失函数会以很多种不同的形式表现出来，分析他们的特点可以帮助进行一些超参数的调整，这里介绍了一些不同图像所揭示的问题。有时候我们会跑出一些奇葩的图，而大多数时候其实也不知道这些奇葩的图意味着什么。

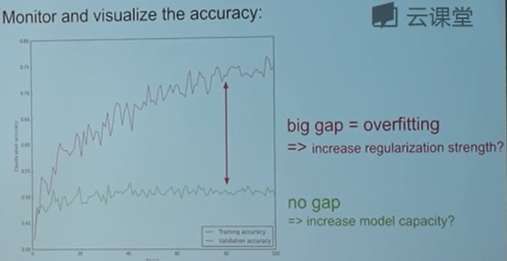
除了损失函数值以外，我们还需要注意准确率的图像，在一些情况下，准确率能解释比损失函数更多的东西。比如在图中训练的正确率在不断的上升，而验证的正确率却保持不变，这就说明大概率出现了过拟合现象。

接下来要关注的是参数的大小及参数更新量之间的区别。

总结一下，这节课讲了神经网络的训练细节。首先是激活函数，最常用的激活函数是Relu。在数据处理环节中，我们的图像用的是去均值方法，使用Xavier初始化做权值初始化，如果网络很小的话，也可以选择一个很小的数，比如0.01作为初始权重。一般都需要用到批量标准化。当我们在做超参数优化的时候，要随机取样超参数，在适当的时候需要使用对数空间。