【课程笔记】反向传播与神经网络初步

第9课 反向传播与神经网络初步

上一节课讲到了评价函数，了解了损失函数。损失函数有两部分组成，数据损失和正则化损失。我们要做的是对损失函数进行优化操作。

计算梯度的方法有两种：

数值梯度：写起来容易，但运算慢

解析梯度：（微积分运算得到）运算快，但有时会出错，所以要进行梯度检查的操作。

强调，在处理程序时，我们更多的要去思考一步一步计算的计算图，而不仅仅是一个复杂的表达式。

参数的值结合一些函数在计算图中会通过计算得到最终的损失函数。表达式一般都非常的简短，但是计算图一般都非常的巨大。但是一些复杂的神经网络结构像图灵机和CNN都没有办法用表达式来表示。而且有时候像在RNN网络里一样，计算图会被重复执行上百次上千次，这个时候我们是没有办法进行公示推导的。所以我们要转换思想，用数据结构的方式去思考它，用一些函数将中间变量转化成最终的损失值。

学习的重点是在计算图中，结合输入和梯度得到最终的选择函数。

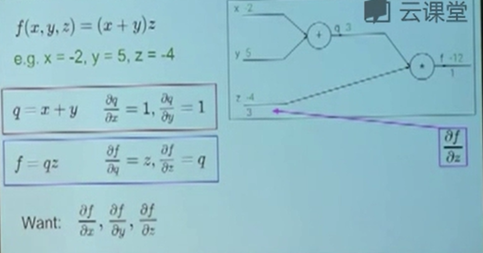
用一个简单的前向传播的例子来说明了一下计算图的运行方式。从左到右的前向传播和从右到左的反向传播。

 

在介绍反向传播的时候，详细介绍了利用求偏导来求梯度的方式，同时也说明了输入参数的变化对于结果变化的影响。

通过计算输出，对于中间参数的偏导和中间参数对不同输入的偏导，就可以使用链式法则计算出输入的参数对于最终结果的影响。链式法则里的每一个中间参数都会对最终结果造成或正或负的影响。

 

这里举了一个例子，将一个复杂的公式转换成了一张计算图，计算了这个图里的所有输入参数对于输出的影响。因为我们知道每一个局部函数的导数怎么求，所以我们最终可以利用链式法则计算出输出对于某一个输入参数的偏导。前向传播计算出了loss函数，然后根据loss函数针对每一层运算计算对输入的梯度。

这里的学生提问让我们知道了前向和反向传播的时间基本上是一样的，但是反向传播会稍慢一点。（冷知识）

讲解了一下BP的分解粒度，可以将一系列的基础运算组合成一个函数，看作是一个基本的处理单元，只要我们能知道这个局部的梯度怎么求，就可以这么做。

这里已经能知道了，之所以要用计算图来思考，是因为它能帮助我直观的理解梯度是如何在整个神经网络里流动的。

这里又举了一个例子，是max函数的梯度怎么计算。对于最大值来说，它的局部梯度是1，而对于较小值来说，它的局部梯度是0。那么max函数就相当于是一个梯度路由，而加法运算则相当于是一个梯度分配器。这只是一个比较直观的理解。

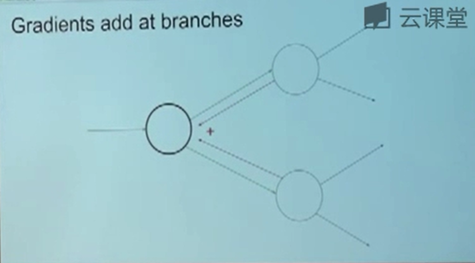
反向传播时，当遇到同一个参数，经过不同的路径对输出产生影响的时候，在计算梯度值的时候需要对他们进行相加。通过学生提问，我们知道计算图中是绝对不会出现回路的。

 

在实际运行中，怎么在计算门的基础上构建整个图形，计算门之间是怎么连接的，这些通常在对象中进行说明，而这个对象有两部分前向传播和反向传播。这里的门和我们通常说的神经网络的层有着相似之处。

接下来介绍了一些门的实现方法，代码，乘法门的前向和反向运行实现。

这里需要注意的是在前向传播时是会存储大量的数据的，在反向传播的过程中会利用这些数据计算梯度。如果我们不进行反向传播的话，其实可以删除很多中间值。所以当我们使用嵌入式设备进行开发的时候，在测试阶段如果不需要反向传播，我们可以修改代码，使耗费的内存更小。

课程实现使用的是torch框架，所以这里简单介绍了一下torch。说明了每一个单位都必须要具备前向传播和反向传播两个功能。