遗传算法(GA)解决函数优化和TSP问题
摘要
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
本文在遗传算法的模式理论的基础上,用Matlab程序实现了遗传算法,实现了5个二维单目标函数优化和解决了20个城市的旅行商问题。并对各种参数对结果的影响进行了数学分析,通过实验研究了应用中的遗传算法性能影响因素。
二维单目标函数优化过程中,基本可以每次都达到全局最优解,并可以在1000代以内收敛,实验结果显示其收敛速度快,结果直观,性能好。
在TSP问题中,通过修改代码中选择函数、交叉函数的选型,解决了陷入局部最优问题,使得最终达到全局最优,且路径图不交叉。
本文整体方案仍然处于实验的阶段,离解决实际问题还有很大的差距。遗传算法的应用在日后必定会越来越成熟,同时这一领域也具有很大的发展空间。
关键词:遗传算法 二维单目标函数优化 Matlab TSP
目录
- 绪论
1.1 课程背景
自然计算(Nature Inspired Computation),具有模仿自然界特点,通常是一类具有自适应、自组织、自学习能力的模型与算法,能够解决传统计算方法难于解决的各种复杂问题。
从自然计算角度看,每种自然计算方法都对应一种实际的启发源,要将启发源中所包含的内在的特殊规律,如生物进化规律、离子进出细胞膜的规律等,利用数学或逻辑符号建模描述成一种特殊计算过程。以自然界包括生命、生物及生态系统,物理与化学,经济以及社会文化系统等,特别是生物体的功能、特点和作用机理为基础,研究其中所蕴含的丰富的信息处理机制,抽取相应的计算模型,设计相应的算法,研制革新计算系统,并在各相关领域加以应用[1]。
自然计算,是智能计算的一部分,自然计算的应用涉及领域很广,在复杂优化问题求解、优化调度控制与故障诊断、智能控制与机器人控制、智能交通、智能建筑、计算机集成制造、智能电网、数据挖掘、模式识别、网络通信与信息安全、工业设计优化、社会经济、金融与管理、生态环境、生物医学医药、新能源与新材料、航空航天与军事等领域均有应用。
自然计算的内容一般包括:人工神经网络,遗传算法,免疫算法,人工内分沁系统,蚁群算法,粒子群算法以及膜计算等等。
其中,遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
1.2 国内外研究概述
遗传算法是由美国的密歇根大学的Holland教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的,它是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法[2]。
在此之后,遗传算法的研究都以理论为主,直到第—届世界遗传算法大会在Pizibao召开后,遗传算法开始被逐步投入到实际运用中。1990年以后,遗传算法迅速发展,在学术研究的理论和应用领域都是一颗新星。当然,人们在对遗传算法有了一定的理论基础后,更热衷于对于其应用的研究。
遗传算法的应用领域主要有以下几个分支:
1、基于遗传算法的机器学习;
2、遗传算法和Fuzzy Reasoning、Neural Network、Chaos Theory等其它智能计算理论相辅相成的发展;
3、遗传算法对于并行计算的研究有重大意义;
4、对人工生命的研究影响意义非凡,人工生命就是用计算机模拟生命的遗传、繁殖现象;
5、遗传算法和进化策略以及进化规划的互相渗透。
除此之外,还有几件事在遗传算法的发展中起到了至关重要的作用。1991年D.Whitey教授在研究旅行商问题时,提出了交叉算子的概念,并且通过实验进行了验证。还有D.H.Ackley提出的SIGH算法,即是著名的随机迭代遗传爬山法,主要采用随机概率的思想,进行选举产生下一代。
参考文献[1]在前人研究的基础上,分析了遗传算法研究方面发表在EI源刊上的文章分布情况,分别从研究内容和应用领域两个方面进行了统计。从研究内容来看,内容涉及物种多样性、测试函数、遗传算子、参数确定等研究内容的文章占较大数量;从应用领域来看,针对遗传算法在生产调度及机器人学方面进行研究的文章占多数,在自动控制、组合优化和图像处理方面的研究也占很大一部分比例。有关遗传算法在函数优化、机器学习、人工生命、数据挖掘及遗传编程方面研究所涉及的文章不是很多。
总而言之,遗传算法的终极目标是为人类呈现一种全新的思维模式,带来真正的计算革命。
1.3 本文的主要研究内容
本文主要分析了遗传算法的运行机理,查阅了相关的参考文献和应用算法,阐述了作者对于遗传算法的原理与应用的理解。并通过实践,将遗传算法有效应用于函数优化和旅行商问题(即TSP问题Traveling Salesman Problem)的分析中,研究了遗传算法在函数优化和解决TSP问题的应用中的性能,并在MATLAB环境中的实现了遗传算法求解函数优化问题和TSP问题,绘制了相关的结果展示曲线,并对结果进行了一定的分析,提出了改进的思路。
1.3 本文的组织结构
以下是本文的主要内容安排:
第一章 绪论,主要介绍了本论文的研究背景与研究意义,简单说明了现阶段该领域的发展状况。
第二章 相关理论与技术。介绍了遗传算法的基本算法流程,分别提出了遗传算法应用于函数优化和TSP问题的解决思路和理论依据。同时在本章的后半部分还介绍了遗传算法在以上两个领域近几年来的发展情况。
第三章 算法的实现与实验结果的分析。实现了算法并进行了实验测试,并探讨了评估模型的各项指标。
第四章 总结和展望。对本文提出的模型与算法进行总结,指出了目前存在的问题,并对下一步研究方向进行讨论。
- 相关理论与技术
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象,在每次迭代中都保留一组候选解,并按某种指标从解群中选取较优的个体,利用遗传算子(选择、交叉和变异)对这些个体进行组合,产生新一代的候选解群。重复此过程,直到满足某种收敛指标为止。
这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。与传统的启发式优化搜索算法相比,遗传算法的主要本质特征在于群体搜索策略和简单的遗传算子。群体搜索使遗传算法得以突破领域搜索的限制,可以实现整个解空间上的分布式信息采集和探索;遗传算子仅仅利用适应值度量作为运算指标进行随机操作,降低了一般启发式算法在搜索过程中对人机交互的依赖。
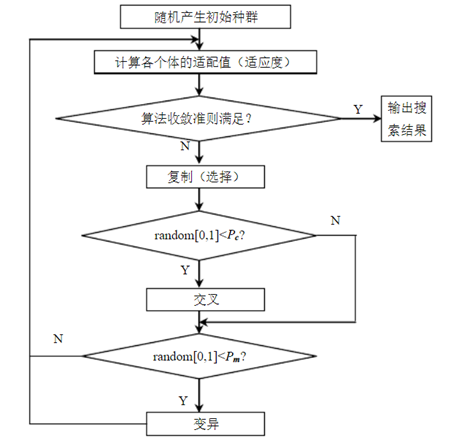
图1.1 标准遗传算法流程图
遗传算法通常实现方式为一种计算机模拟,是计算数学中用于解决最佳化的搜索算法。对于一个最优化问题,一定数量的候选解(称为个体)可抽象表示为染色体,使种群向更好的解进化。传统上,解用二进制表示(即0和1的串),但也可以用实数编码等其他表示方法。进化从完全随机个体的种群开始,之后一代一代发生。在每一代中评价整个种群的适应度,从当前种群中随机地选择多个个体(基于它们的适应度),通过自然选择和突变产生新的生命种群,该种群在算法的下一次迭代中成为当前种群。
相关概念的类比见下列表:
- 群体: 搜索空间的一组有效解;
- 种群: 选择得到的新群体;
- 染色体: 优化问题的可行解的编码串;
- 基因: 染色体的一个编码单元;
- 适配值: 染色体的适应值;
- 交叉: 染色体交换部分基因得到的新染色体;
- 变异: 染色体某些基因的数值改变;
- 进化结束:算法结束,算法收敛。
2.1 遗传算法步骤简介
编码和产生初始群体
染色体一般被表达为简单的字符串或数字串,不过也有其他的依赖于特殊问题的表示方法适用,这一过程称为编码。根据问题选择相应的编码方法,并随机产生一个确定长度的N个染色体组成的初始群体。常用的编码方式如下:
二进制编码方法是使用二值符号集{0,1},它所构成的个体基因型是一个二进制编码符号串。二进制编码符号串的长度与问题所要求的求解精度有关。
优点是简单。无论是编码还是解码操作都非常方便和快捷;方便交叉和变异;符合最小字符集编码原则。缺点是不适合连续函数的优化问题,局部搜索能力差;连续的数值之间有时候存在海明距离大的问题。例如63和64对应的二进制分别是0111111和1000000。(连续数值对应的二进制数7位全都不同)对于高精度的问题,变异后可能会出现远离最优解的情况,表现型不稳定。
实数编码方法,个体基因值用某范围内的一个实数来表示。编码长度等于决策变量的个数。
优点是精度高,适用于连续变量问题,避免了海明悬崖问题;适用于表示范围比较大的数值,适合空间较大的一串算搜索;降低了计算复杂性,提升效率;便于遗传算法与经典优化方法的混合使用;便于设计针对问题的专门知识的知识型遗传算子;便于处理复杂的决策变量约束条件,适合于组合优化问题。
排列编码方法,排列编码主要针对一些特殊问题。将有限集合的元素尽心排列。假如集合内有m个元素,那么就有m!个排列组合。
优点是对于NPhard问题,m较大,穷举法失效,这时就可以用遗传算法。常见的应用有旅行商(TSP)问题、作业调度(job-scheduling)问题以及资源调度(resource-scheduling)问题等。
本文中在
产生初始化种群是在可行域内产生若干个可行解,采用随机初始化的方法。算法随机生成一定数量的个体,可能出现比较极端的情况,但是大概率情况下,这些使用随机数函数产生的可行解,在可行域内是均匀分布的。有时候操作者也可以干预这个随机产生过程,以提高初始种群的质量。
设计适应度函数
个体的适应度(fitness)指的是个体在种群生存的优势程度度量,用于区分个体的"好与坏"。适应度使用适应度函数(fitness function)来进行计算。适应度函数也叫评价函数,主要是通过个体特征从而判断个体的适应度。对群体中的每一个染色体计算它的适应度的一般过程:
- 对个体编码串进行解码处理后,可得到个体的表现型。
- 由个体的表现型可计算出对应个体的目标函数值。
- 根据最优化问题的类型,由目标函数值按一定的转换规则求出个体的适应度。
在设计适应度函数的时候,应满足以下要求:单值、连续、非负、最大化、合理、一致性、计算量尽可能小、通用新尽可能强等。
在每一代中,都会评价每一个体,并通过计算适应度函数得到适应度数值。按照适应度排序种群个体,适应度高的在前面。这里的"高"是相对于初始的种群的低适应度而言。
设计收敛准则[5],开始搜索
初始的数据可以通过这样的选择过程组成一个相对优化的群体。之后,被选择的个体进入交叉过程。这个过程是通过选择和繁殖完成,其中繁殖包括交叉和突变,产生下一代个体并组成种群。
一代一代向增加整体适应度的方向发展,直到满足收敛准则或者达到迭代次数。因为总是更常选择最好的个体产生下一代,而适应度低的个体逐渐被淘汰掉。
一般收敛准则有以下几种:
- 进化次数限制;
- 计算耗费的资源限制(例如计算时间、计算占用的内存等);
- 一个个体已经满足最优值的条件,即最优值已经找到;
- 适应度已经达到饱和,继续进化不会产生适应度更好的个体;
- 人为干预;
- 以及以上两种或更多种的组合。
交叉操作
一般的遗传算法都有一个交叉概率(又称为交叉概率),范围一般是0.6~1,这个交叉概率反映两个被选中的个体进行交叉的概率。例如,交叉概率为0.8,则80%的"父代"会产生子代。每两个个体通过交叉产生两个新个体,代替原来的个体,而不交叉的个体则保持不变。交叉的两个父代染色体相互交换,从而产生两个新的染色体。
本文中使用单点交叉的方法,第一个个体前半段是父亲的染色体,后半段是母亲的,第二个个体则正好相反。不过这里的半段并不是真正的一半,交叉的位置叫做交叉点,也是随机产生的,可以是染色体的任意位置。
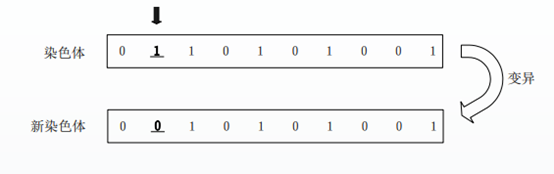
变异操作
通过突变产生新的"子"个体。一般遗传算法都有一个固定的较小的变异概率,一般取0.0001-0.1,这代表变异发生的概率。根据这个概率,新个体的染色体随机的突变,突变后的个体和未产生突变的个体一起,形成新的群体。
本文采用的方法是随机改变染色体的一个字节(0变到1,或者1变到0)。
选择操作
选择则是根据新个体的适应度进行,但同时不意味着完全以适应度高低为导向,因为单纯选择适应度高的个体将可能导致算法快速收敛到局部最优解而非全局最优解,我们称之为早熟。作为折中,遗传算法依据原则。适应度越高,被选择的机会越高,而适应度低的,被选择的机会就低。
带选择、交叉、变异的标准遗传算法并不一定收敛于全局最优解。在实际的应用过程中,要对各种参数进行适当的改进,才能使遗传算法具有良好的收敛性能。
2.2 遗传算法解决函数优化问题
 函数优化问题是遗传算法的经典应用领域,也是对遗传算法进行性能评价的常用算例[3]。在使用遗传算法解决函数优化问题中,本文使用基本的遗传算法解决了二位测试函数的优化问题。
函数优化问题是遗传算法的经典应用领域,也是对遗传算法进行性能评价的常用算例[3]。在使用遗传算法解决函数优化问题中,本文使用基本的遗传算法解决了二位测试函数的优化问题。
在使用遗传算法解决函数优化问题的时候,算法的主要部分如下:
在编码过程中,采用了二进制编码方式,由于上述函数两个变量x与y的取值范围都是相同的且是对称的,并且变量的取值区间也都不大,因此采用同样的编码长度。x与y均使用20位二进制进行编码。
设定搜索次数为N,程序完成N次搜索之后取出最优适应函数值、最优值对应的个体编码。N的值随不同函数调整。
计算的是每个个体之前所有个体的选择概率之和,相当于概率论中的概率分布函数F(x)。
设计适应度函数Fit(x)时可以对目标函数稍作调整,使得Fit(x)越大,证明个体越好。在这里,简单进行举例,当需要控制更优秀的个体的适应度更大时,相关调整的方法如下:
由于本文中要针对5个不同的单目标函数优化问题编写代码,在初步使用Matlab绘制出函数的三维图像之后,发现函数优化过程均需要求得函数在可行域中的最小值,因此代码部分和适应度函数设计部分可以统一。
因此本文在设计适应度函数时,设计的规则是Fit(x)大多数为目标函数的倒数,Fit(x)越大,证明个体越好。
2.3 遗传算法解决TSP问题
旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
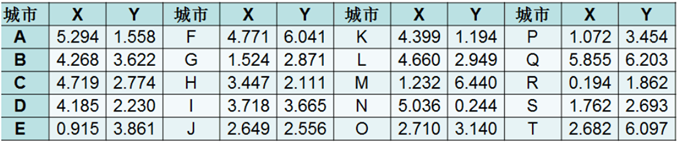
一个商人欲到20个城市推销商品,每两个城市i和j之间的距离为,如何选择一条道路使得商人每个城市走一遍后回到起点且所走路径最短?
设定搜索次数为G,程序完成G次进化之后取出最短路径,画出相关图像。
这时随机选择两个交叉位置a和b,比如说a=3,b=6,那么交叉的片段为:
然后将父代2的交叉片段移动到父代1的前面,将父代1的交叉片段移动到父代2的前面,则这两个父代个体变为:
然后从前到后把第2个重复的基因位删除掉,我们先把两个父代个体中重复的基因位标记出来:
比如说有6个城市,当前解为123456,我们随机选择两个位置,然后将这两个位置上的元素进行交换。
比如说,交换2和5两个位置上的元素,则交换后的解为153426。
有6个城市,当前解为123456,我们随机选择两个位置,然后将这两个位置之间的元素进行逆序排列。
比如说,逆转2和5之间的所有元素,则逆转后的解为154326。
有6个城市,当前解为123456,我们随机选择两个位置,然后将这第一个位置上的元素插入到第二个元素后面。
比如说,第一个选择2这个位置,第二个选择5这个位置,则插入后的解为134526。
在变异操作中,我们将以上三种操作赋予不同的权重,然后采用轮盘赌的方式选择究竟使用哪个操作。
一个个体的目标函数值就是该个体的总距离,比如说一个个体为213,那么这个个体的总距离=21之间的距离+13之间的距离+32之间的距离(从3出发还需要返回起始点2)。
而一个个体的适应度值是其目标函数值的倒数。因为总距离越小说明这个个体质量越好,所以适应度值越大就说明这个个体质量越好。
3.1解决二维单目标函数优化算法设计及结果分析
由于本文中要针对5个不同的单目标函数优化问题编写代码,在初步使用Matlab绘制出函数的三维图像之后,发现函数优化过程均需要求得函数在可行域中的最小值,因此代码部分和适应度函数设计部分可以统一。
a)初始化:设置进化代数计数器i=0,设置最大进化代数N,随机生成num个个体作为初始群体P(0)。
d)交叉运算:将单点交叉算子作用于群体。
e)变异运算:将变异算子作用于群体。
群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。
f)终止条件判断:若i=N,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
对于二维球形函数:
在编码过程中,x与y均使用20位二进制进行编码,编码总位数40位。随机产生10个初始种群。
设定搜索次数为N=5000,程序完成N次搜索之后取出最优适应函数值、最优值对应的个体编码。
在进行函数优化的时候,采用单点交叉的方法,交叉概率。对于交配后新种群中个体的每一位基因,根据变异概率随机决定该基因是否进行变异,选择时采用轮盘赌选择方法。
设计目标函数使得Fit(x)= 越大,证明个体越好。
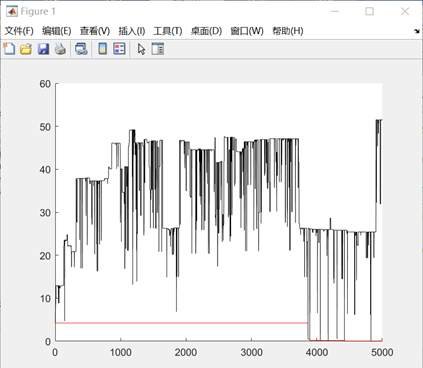
图3.1.1 函数1优化过程中目标函数最优值变化
由上图可以看到,优化过程中函数的值一直在随机变化,但是最优值确实在变小。
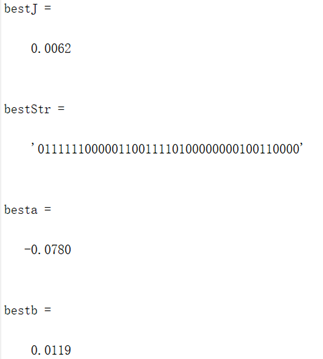
编写代码将全局最优值结果打印出来,其中"bestJ"对应的是目标函数的最优值,"bestStr对应的是最优个体基因的编码串,"besta"与"bestb"分别对应取最优值时x和y的取值(基因串解码的结果)。并将结果在函数图像中绘制出来。


图3.1.2 函数一最优点位置图及计算机结果
算法得到的目标函数在可行域内的最优解为(-0.078,0.011),最佳目标函数值为0.0062,近似等于可行域内最小目标函数值。
对于De-Jong函数:
在编码过程中,x与y均使用20位二进制进行编码,编码总位数40位。设定搜索次数为N=10000,单点交叉的方法,交叉概率。对于交配后新种群中个体的每一位基因,根据变异概率随机决定该基因是否进行变异,选择时采用轮盘赌选择方法。
设计目标函数使得Fit(x)= 越大,证明个体越好。
同上述函数,编写代码将全局最优值结果打印出来,并将结果在函数图像中绘制出来。
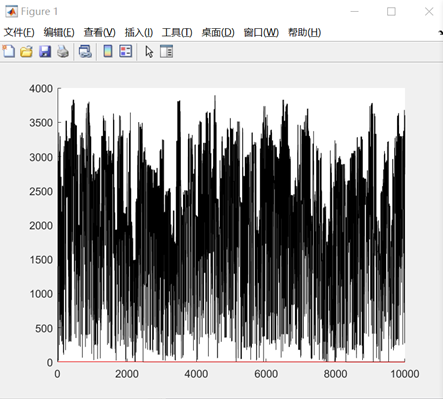
图3.2.1 函数2优化过程中目标函数值变化
由上图可以看到,优化过程中函数的值一直在随机变化,但是目标函数的最优值确实在变小。
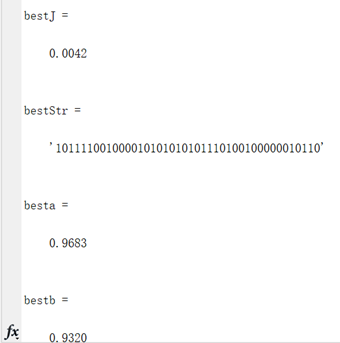

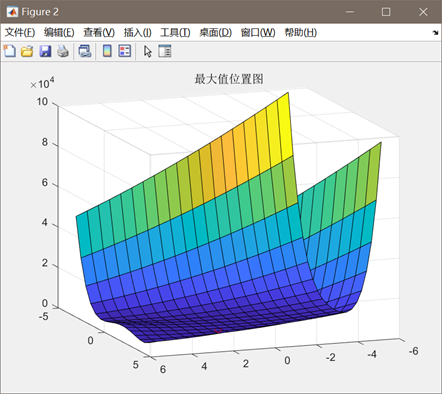
图3.2.2 函数2最优点位置图及计算结果
算法得到的目标函数在可行域内的最优解为(0.9683,0.9320),最佳函数值为0.0042,近似等于可行域内最小目标函数值。
对于Goldstein--price函数:
在编码过程中,x与y均使用20位二进制进行编码,编码总位数40位。设定搜索次数为N=1000,单点交叉的方法,交叉概率。对于交配后新种群中个体的每一位基因,根据变异概率随机决定该基因是否进行变异,选择时采用轮盘赌选择方法。
设计目标函数,由于函数有一部分值比0小,而适应度函数一定是正的,因此,此时根据函数值的取值范围,设计适应度函数为
Fit(x)=
使得适应度函数值越大,目标函数值越小,证明个体越好。
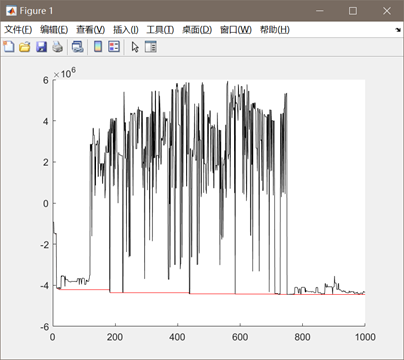
图3.3.1 函数3优化过程中目标函数值变化
同上述函数,编写代码将全局最优值结果打印出来,并将结果在函数图像中绘制出来。这里对部分变量名进行了修改,"bestF"对应目标函数的最优值,"bestx"与"besty"分别对应取最优值时x和y的取值(基因串解码的结果)。并将结果在函数图像中绘制出来。
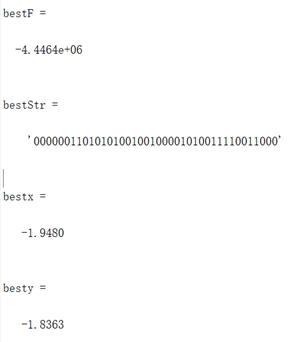
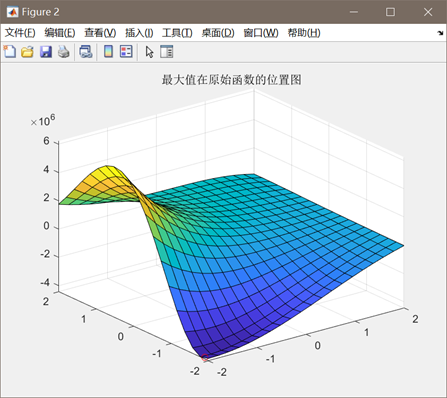
图3.3.2 函数3最优点位置图及计算结果
算法得到的目标函数在可行域内的最优解为(-1.9480,-1.8363),最佳目标函数值为-4.4464*106,近似等于可行域内最小目标函数值。
对于Himmelbaut函数:
在编码过程中,x与y均使用20位二进制进行编码,编码总位数40位。设定搜索次数为N=1000,单点交叉的方法,交叉概率。对于交配后新种群中个体的每一位基因,根据变异概率随机决定该基因是否进行变异,选择时采用轮盘赌选择方法。
设计目标函数使得Fit(x)=越大,证明个体越好。
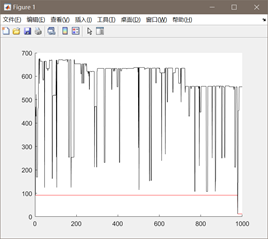
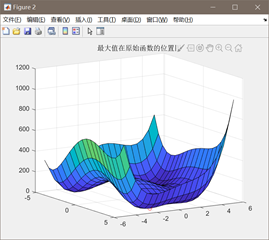
图3.4.1 函数4优化过程中目标函数值变化及最优点计算结果
同上述函数,编写代码将全局最优值结果打印出来,并将结果在函数图像中绘制出来。从函数4优化过程中适应度值函数的变化过程可以看出,在进化临近1000次的时候,目标函数值有一个较大的降低,达到最优值2.26,因此猜测此时并未达到全局最优解。
决定再次训练,多进化几个轮次,观察目标函数值是否会再变小一点。将进化终止条件调整到5000次,重复进行实验,得到如下结果:
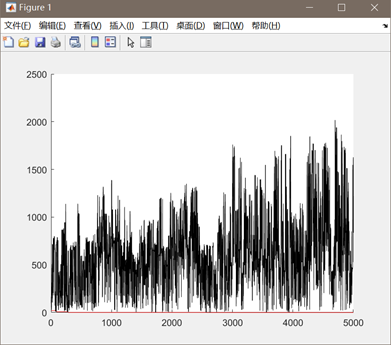
图3.4.2 函数4再次优化过程中目标函数值变化
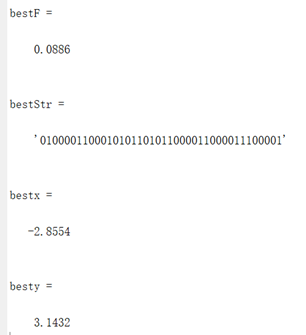
此时的最优值下降到了0.0886,相比之前得到的局部最优值2.26得到了很多优化。因此可以判定,增加进化次数有助于函数得到全局的最优值。

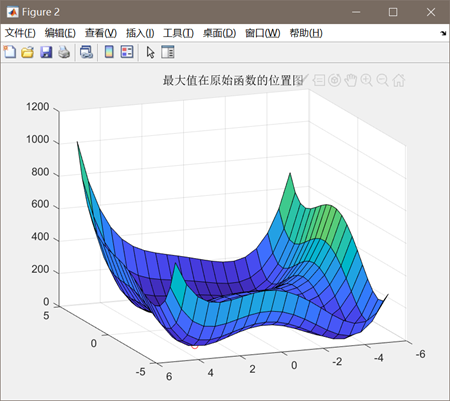
图3.4.3 函数4最优点位置图及计算结果
算法得到的目标函数在可行域内的最优解为(-2.8554,3.1432),最佳目标函数值为0.0886,近似等于可行域内最小目标函数值。
对于函数Six-hump cameback函数
在编码过程中,x与y均使用20位二进制进行编码,编码总位数40位。设定搜索次数为N=1000,单点交叉的方法,交叉概率。对于交配后新种群中个体的每一位基因,根据变异概率随机决定该基因是否进行变异,选择时采用轮盘赌选择方法。
设计目标函数使得适应度函数Fit(x)= 越大,证明个体越好。
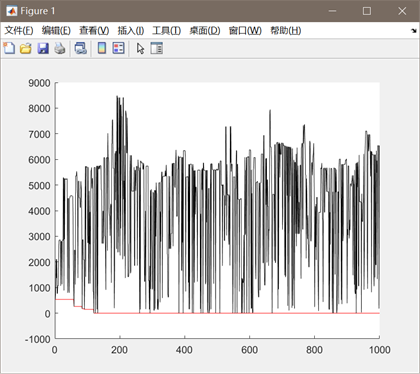
图3.5.1 函数5优化过程中目标函数值变化
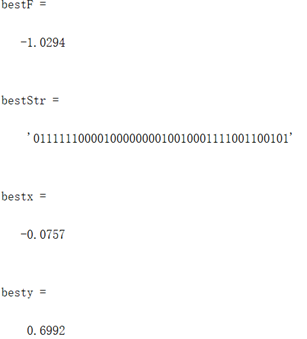
同上述函数,编写代码将全局最优值结果打印出来,并将结果在函数图像中绘制出来。

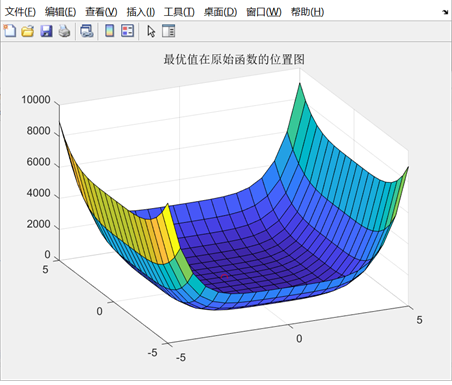
图3.5.2 函数5最优点位置图及计算结果
算法得到的目标函数在可行域内的最优解为(-0.0757,0.6992),最佳目标函数值为-1.0294,近似等于可行域内最小目标函数值。
解决TSP问题算法设计及结果分析
前期准备:首先在程序中导入20个城市的坐标,根据坐标计算出任意两个城市之间的距离的距离矩阵。同时根据城市的坐标绘制出城市的分布图。
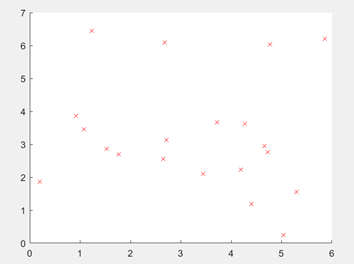
图3.6.1 20城市的坐标分布图
种群初始化:解决TSP问题过程中个体编码方法为排列编码。对于20个城市的TSP问题,编码为1~20的整数的随机排列。
初始化的参数有种群规模、染色体基因个数(即城市的个数)、最大遗传代数、交叉概率、变异概率。
随机选择一个种群,绘制出其对应的城市连线线路图。
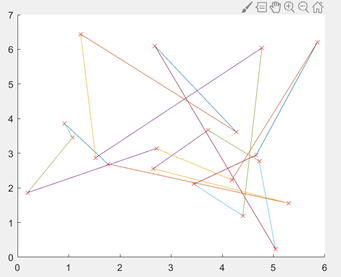
图3.6.2 20城市初始化编码的路径图
适应值函数:由于之前已经计算出任意两个城市之间的距离,因此每个染色体(即n个城市的随机排列)可计算出总路径长度,作为目标函数。因此可将一个随机全排列的总距离的倒数作为适应度函数,即距离越短,适应度函数越好,满足TSP要求。
交叉操作:本文算法采用OX交叉操作,随机选择两个个体,在对应位置交换若干个基因片段,同时保证每个个体依然是1~20的随机排列,防止进入局部收敛。
变异操作:将变异算子作用于群体,并通过以上运算得到下一代群体。
选择操作:采用赌轮选择机制,使适应度较大(优良)个体有较大的存在机会,而适应度较小(低劣)的个体继续存在的机会也较小。
保留每代最优个体,算出目标函数值,绘制目标函数值的进化曲线。
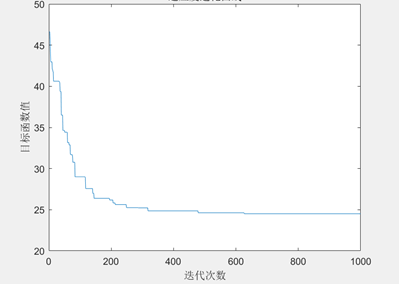
图3.6.3 TSP问题目标函数值进化曲线
可以看到,随着进化代数的增加,总距离的值不断下降,说明遗传算法可以解决TSP问题。
编写代码计算出优化后的最短距离和画出最短路径图。
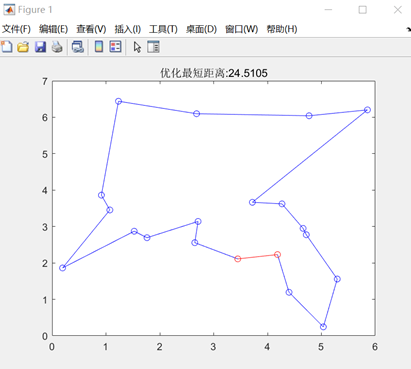
图3.6.4 优化后的最短距离和最短路径图
由于遗传算法具有随机性,在同等参数下,程序计算出的最小路径可能会存在差别,如下图:
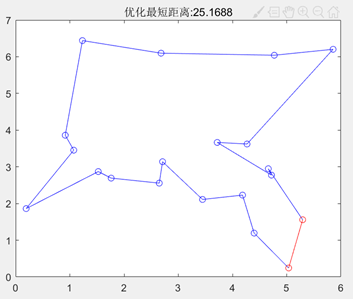
图3.6.5 同一代码同参数不同输出结果
此时种群规模为200,进化代数为1000。为了加深对于遗传算法的理解,我进行了不同种群规模的实验,染色体基因个数(即城市的个数)、最大遗传代数、交叉概率、变异概率结果如下图:
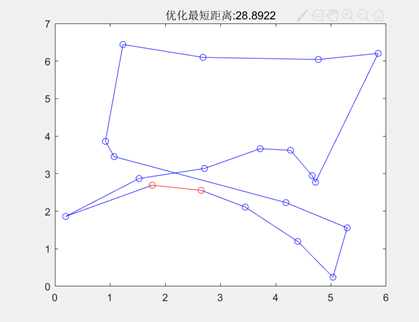
种群规模=50
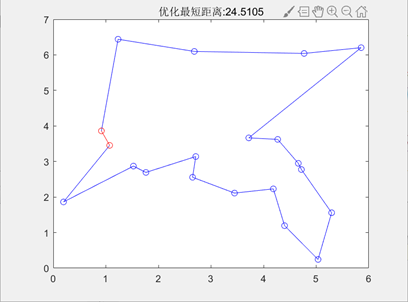
种群规模=500
图3.6.6种群规模不同时的不同输出结果
由运行结果可知当种群规模较小时(50个个体)得到TSP的最短路径长度均小于全局的最短路径长度。
因此,可以推断,在最大遗传代数足够的情况下,群体个数M参数不宜过小,设置较小,虽然降低了计算量,但是同时降低了每次进化中群体包含更多较好染色体的能力。
也不宜过大,若设置较大,一次进化所覆盖的模式较多,可以保证群体的多样性,从而提高算法的搜索能力,但是由于群体中染色体的个数较多,势必增加算法的计算量,降低了算法的运行效率。
同时,在种群规模为200,其他参数不变,改变最大遗传代数后,得到结果如下图:

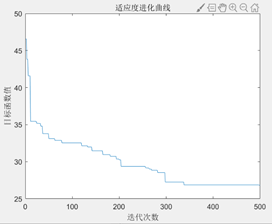
最大遗传代数=500
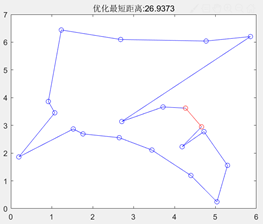
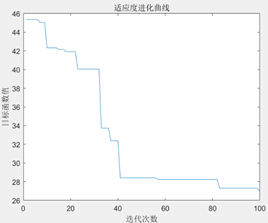
最大遗传代数=100
图3.6.7 改变最大遗传代数后的结果图
由以上结果图可知,最大遗传代数不宜太小,否则可能还没有找到最优值,算法就停止了搜索。
同理也进行了交叉概率、变异概率对结果的影响的一系列实验,得出以下结论:
影响着算法的运行效率,但其大小对得出的最短路径长度的大小并没有直接的影响,不能保证其最优性。Pc的取值为0.4~0.99时效果较好。
的值不宜过大,最好取0.001-0.1。因为变异对已找到的较优解具有一定的破坏作用,如果的值太大,可能会导致算法目前所处的较好的搜索状态倒退回原来较差的情况。
在TSP问题中,一开始编写的代码,即使加大迭代次数到5000,也不能解决的最短路径的交叉问题,使得最终得到的最短路径值比较大。陷入了局部最优。通过修改代码中选择函数、交叉函数的选型,解决了问题,使得最终得到的最短路径值更小,且路径图不交叉。

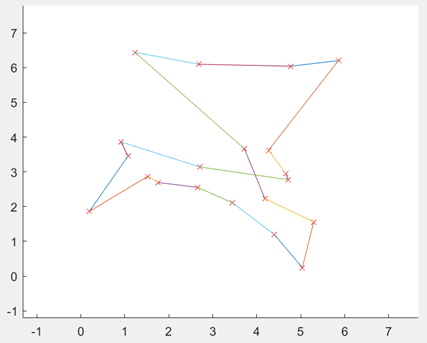
图3.6.8 未改良的算法运行结果
- 总结与展望
4.1 总结
本文在遗传算法的模式理论的基础上,用Matlab程序实现了遗传算法,并对各种参数对结果的影响进行了数学分析,通过实验研究了应用中的遗传算法性能影响因素。
在二维单目标函数优化过程中,虽然函数有很多局部最优,但加大迭代次数后,也基本可以每次都达到全局最优解,并可以在1000代以内收敛,实验结果显示其收敛速度快,结果直观,性能好。
在TSP问题中,通过修改代码中选择函数、交叉函数的选型,解决了局部最优问题,使得最终达到全局最优,且路径图不交叉。
理解了遗传算法的独有特点:
- 从问题解的串集开始搜索,而不是从单个解开始。这是遗传算法与传统优化算法的极大区别。传统优化算法是从单个初始值迭代求最优解的;容易误入局部最优解。遗传算法从串集开始搜索,覆盖面大,利于全局择优。
- 遗传算法同时处理群体中的多个个体,即对搜索空间中的多个解进行评估,减少了陷入局部最优解的风险,同时算法本身易于实现并行化。
- 遗传算法基本上不用搜索空间的知识或其它辅助信息,而仅用适应度函数值来评估个体,在此基础上进行遗传操作。适应度函数不仅不受连续可微的约束,而且其定义域可以任意设定。这一特点使得遗传算法的应用范围大大扩展。
- 遗传算法不是采用确定性规则,而是采用概率的变迁规则来指导他的搜索方向。
- 具有自组织、自适应和自学习性。遗传算法利用进化过程获得的信息自行组织搜索时,适应度大的个体具有较高的生存概率,并获得更适应环境的基因结构。
本次大作业完成的过程并没有想象中的顺利,遇到了很多问题。一开始参考网络上的开源代码,但是结果并不理想。在重新仔细研究了一遍遗传算法后,对于基因长度的选择,选择算子,交叉算子等相关内容有了更深刻的认识。
在之后针对每个函数进行优化时,多次尝试了不同的参数值,对于参数的选择以及不同参数对于算法性能的影响有了更全面的了解。
4.2 展望
本文在运用遗传算法求解问题时,选择参数经验较少,需要通过查阅资料获得相关最优参数取值范围。同时我也在反思这种经验主义或盲目性,遗传算法是否可以和梯度下降算法自适应学习率一样,自主动态调整参数?能否结合直观的参数关系图和统计分析,以寻找解决函数优化问题的最优交叉和变异率的组合参数的有效方法。
在二维单目标函数初始化的时候,可以不随机产生初始编码值,而是依据先验经验,在更小的最优解可能出现的局部区域展开更加细致的搜索。
算法本身也可以采用动态自适应技术,在进化过程中自动调整算法控制参数和编码精度,比如使用模糊自适应法。
旅行商问题是一类经典的组合最优化问题,在理论研究和实际应用领域具有重要的研究价值。传统的遗传算法GA在求解TSP问题时容易出现早熟和陷入局部最优等现象(实验过程中曾遇到过)。
为此查阅了很多资料,得知了一些优化方法:一种基于协同进化的遗传算法(CEGA)用于解决GA算法的缺陷[10]。实验结果表明,所提出的算法[10]在解决TSP问题时,具有收敛速度快、容易跳出局部最优等特点,相较其他GA算法具有更好的性能。除此之外还有一种基于自适应层次谱聚类与遗传优化的算法求解大规模TSP算法[8],一种自适应遗传算法,变异率自适应,提高了算法的收敛速度【12】。
总之,通过本次大作业,我对于遗传算法有了更加深入的认识。同时,也完成了一系列的相关实验,提高了代码能力。但是在实验中碰到的问题也让我明白,本次大作业只是一个开始,遗传算法的魅力远不止此,可以提升、可以探索的空间还相当的大。本文整体方案仍然处于实验的阶段,离解决实际问题还有很大的差距。
遗传算法的应用在日后必定会越来越成熟,同时这一领域也具有很大的发展空间,在未来我也将投入更多的精力在这个方面,也期望未来可以取得更高的成就。
参考文献
- 自然计算的研究综述[J]. 电子学报, 2012, 40(3):548-558.
https://wenku.baidu.com/view/59ef836e590216fc700abb68a98271fe910eaf92.html
- 马永杰, 云文霞,MA Yong-jie, YUN Wen-xia- 《计算机应用研究》2012年4期
- 蒋冬初. 遗传算法及其在函数优化问题中的应用研究[D].湖南大学,2004.
- 石丽娟. 遗传算法求解函数优化问题的Matlab实现. 福建电脑, 2010年6期
- 王辉, 徐晓英. 基于遗传算法收敛特性的停机准则[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(005):1091-1094.
- 王辉, 徐晓英基于遗传算法收敛特性的停机准则. 《武汉理工大学学报(交通科学与工程版)》 2012年05期
- 李庆,魏光村,高兰,仇国华,肖新光.用于求解TSP问题的遗传算法改进[J].软件导刊,2020,19(03):116-119.
- 杨彩虹,杨明.基于自适应层次谱聚类与遗传优化的TSP算法[J].云南师范大学学报(自然科学版),2020,40(01):44-51.
- 遗传算法交叉算子的性能研究,益阳师专学报2002.19(3):26-28
- 王震,刘瑞敏,朱阳光,王枭.一种求解TSP问题的改进遗传算法[J].电子测量技术,2019,42(23):91-96.
- 遗传算法的收敛性分析,湖南教育学院学报2002.20(4):285-288
- 刘景鑫,李林林,李治华,张耘赫.一种求解旅行商问题的基于外部存档的自适应遗传算法[J].计算机时代,2019(07):51-53.
- 遗传算法在实际应用中的性能分析,吉首大学学报2003.24(3):12-14
- 遗传算法并行机理分析,海南大学学报2004.22(4):331-335
- 遗传算法在求解函数优化中的最优化参数研究2005年4月
附录
任务一:遗传算法计算函数最优值代码
一共五个函数,都是求最小值,因此只需要修改适应度函数的表达式、目标函数的表达式、可行域的范围,和调整交叉概率、变异概率、进化次数等参数即可。
主函数
%%%%%%%%%%%%%%%遗传算法解决函数优化问题%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%six-hump函数%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
%%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%%%%%%%%%
Pc=0.9; %交叉概率
Pm=0.01; %变异概率
N=1000;%迭代次数
Num=40;%编码总位数
Num1=20;%x编码位数
a1=-5; %x下限
b1=5; %x上限
a2=-5; %y下限
b2=5; %y上限
%%%%%%%%%%%%%%%%%%%%随机生成初始字符串%%%%%%%%%%%%%%%%%%%%%
for i=1:10 %生成10个长度为Num的随机0/1字符串
a = round(rand(1,Num)*1);
a = num2str(a);
a(a==' ')=[];
s{i}=a;
end
%%%%%%%%%%%%进化过程,迭代N次后结束%%%%%%%%%%%%%
for i=1:N
s1=s;
for j=1:10
J(j)=fitness(s1{j});
end
s = crossover(Pc,s,J); %交叉
s = mutation(Pm,s); %变异
s = selection(s,J); %选择
for j=1:10
J(j)=fitness(s{j});
end
[mi,I]=min(J);
TempMin(i)=mi;
Minstr{i}=s{I};
best(i)=min(TempMin);
end
%%%%%%%%%%%%%%%%%%%%%画出优化图线%%%%%%%%%%%%%%%%%%%%%
figure();
t=1:N;
hold on
plot(t,best,'r',t,TempMin,'k');
[mi,I]=min(TempMin);
bestF=min(TempMin)%打印最优值目标函数值
bestStr=Minstr{I}%打印最优值的编码串
x1=bestStr(1:Num1);
x2=bestStr(Num1+1:Num);
n=bin2dec(x1);
m=bin2dec(x2);
bestx=a1+[(b1-a1)*n/(2^Num1-1)] %打印出最佳x值
besty=a2+[(b2-a2)*m/(2^(Num-Num1)-1)] %打印出最佳y值
%%%%%%%%%%%画出函数图像,并标出最优值点%%%%%%%%%%%%%%%%%%
figure();
x1=linspace(-5,5,20);
x2=linspace(-5,5,20);
[x,y]=meshgrid(x1,x2);
for i=20:-1:1
for j=20:-1:1
ax=x(i,j);
by=y(i,j);
z(i,j)=4*ax^2+2.1*ax^4+(1/3)*ax^6+ax*by-4*by^2+4*by^4;
end
end
surf(x,y,z);
hold on;
plot3(bestx,besty,bestF, 'ro');title('最优值在原始函数的位置图');
适应度值函数
%%%%%%%%%%%%%%%%计算目标函数%%%%%%%%%%%%%%%%
function y=fitness(b)
a1=-5; %x下限
b1=5; %x上限
a2=-5; %y下限
b2=5; %y上限
Num=40;%编码总位数
Num1=20;%x编码位数
x1=b(1:Num1);
x2=b(Num1+1:Num);
n=bin2dec(x1);
m=bin2dec(x2);
ax=a1+[(b1-a1)*n/(2^Num1-1)];
by=a2+[(b2-a2)*m/(2^(Num-Num1)-1)];
y=4*ax^2+2.1*ax^4+(1/3)*ax^6+ax*by-4*by^2+4*by^4;
单点交叉函数
%%%%%%%%%%%%%%%%%单点交叉函数%%%%%%%%%%%%%%%%%%
function y=crossover(Pc,s,J)
Num=40;%编码总位数
Num1=20;%x编码位数
for i=1:10
if Pc>rand(1)
j=randi(10,1);
k=randi(10,1);
if j~=k
S1 = s{j};
S2 = s{k};
h = randi([2,Num-1],1);
new1 = [S1(1:h),S2(h+1:Num)];
new2 = [S2(1:h),S1(h+1:Num)];
s{j}=new1;
s{k}=new2;
end
end
end
y=s;
轮盘赌选择函数
%%%%%%%%%%%%%%%%%轮盘赌选择函数%%%%%%%%%%%%%%%%%
function y=selection(s,J)
F = sum(J);
for j=1:10
p(j)=J(j)/F;
end
LJ=zeros(1,20);
LJ(1)=p(1);
for i=2:10
LJ(i)=LJ(i-1)+p(i);
end
for i=1:10
sjs=rand(1);
for j=1:9
if LJ(j)>sjs
live{i}=s{j};
break;
end
if LJ(j)<=sjs&&sjs<LJ(j+1)
live{i}=s{j+1};
break;
end
end
end
y=live;
end
变异函数
%%%%%%%%%%%%%%%%%%%%%%%%%变异函数%%%%%%%%%%%%%%%%%%%%%%%
function y=mutation(Pm,s)
Num=40;%编码总位数
Num1=20;%x编码位数
for i=1:10
for j=1:Num
if Pm>rand(1)
S=s{i};
mid=str2num(S(j));
mid=1-mid;
S(j)=num2str(mid);
s{i}=S;
end
end
end
y=s;
任务二:遗传算法计算TSP最短路径代码
主函数
%%%%%%%%%%%%%%%%%%遗传算法解决TSP问题%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
C=[
5.294 1.558;
4.268 3.622;
4.719 2.774;
4.185 2.230;
0.915 3.861;
4.771 6.041;
1.524 2.871;
3.447 2.111;
3.718 3.665;
2.649 2.556;
4.399 1.194;
4.660 2.949;
1.232 6.440;
5.036 0.244;
2.710 3.140;
1.072 3.454;
5.855 6.203;
0.194 1.862;
1.762 2.693;
2.682 6.097;
]; %20个城市坐标
N=size(C,1); %TSP问题的规模,即城市数目
D=zeros(N); %任意两个城市距离间隔矩阵
%%%%%%%%%%%%%求任意两个城市距离间隔矩阵%%%%%%%%%%%%%%%%%%%%%
for i=1:N
for j=1:N
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
end
end
NP=200; %种群规模
G=1000; %最大遗传代数
f=zeros(NP,N); %用于存储种群
F=[]; %种群更新中间存储
for i=1:NP
f(i,:)=randperm(N); %随机生成初始种群
end
R=f(1,:); %存储最优种群
len=zeros(NP,1); %存储路径长度
fitness=zeros(NP,1); %存储归一化适应值
gen=0;
%%%%%%%随机选择一个种群,画出所有城市坐标,对应各城市之间的连线%%%%%%%%%%%
R=f(1,:);
figure(1);
scatter(C(:,1),C(:,2),'rx');
figure(2);
plot_route(C,R);
%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%
while gen<G
%%%%%%%%%%%%%%%%%计算路径长度%%%%%%%%%%%%%%%%%%%%%
for i=1:NP
len(i,1)=D(f(i,N),f(i,1));
for j=1:(N-1)
len(i,1)=len(i,1)+D(f(i,j),f(i,j+1));
end
end
maxlen=max(len); %最长路径
minlen=min(len); %最短路径
%%%%%%%%%%%%%%%%%%%%更新最短路径%%%%%%%%%%%%%%%%%%%
rr=find(len==minlen);
R=f(rr(1,1),:);
%%%%%%%%%%%计算归一化适应值%%%%%%%%%%%%%%%%%%%%
for i=1:length(len)
fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.001)));
end
%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%
nn=0;
for i=1:NP
if fitness(i,1)>=rand
nn=nn+1;
F(nn,:)=f(i,:);
end
end
[aa,bb]=size(F);
while aa<NP
nnper=randperm(nn);
A=F(nnper(1),:);
B=F(nnper(2),:);
%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%
W=ceil(N/10); %交叉点个数
p=unidrnd(N-W+1); %随机选择交叉范围,从p到p+W
for i=1:W
x=find(A==B(p+i-1));
y=find(B==A(p+i-1));
temp=A(p+i-1);
A(p+i-1)=B(p+i-1);
B(p+i-1)=temp;
temp=A(x);
A(x)=B(y);
B(y)=temp;
end
%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%
p1=floor(1+N*rand());
p2=floor(1+N*rand());
while p1==p2
p1=floor(1+N*rand());
p2=floor(1+N*rand());
end
tmp=A(p1);
A(p1)=A(p2);
A(p2)=tmp;
tmp=B(p1);
B(p1)=B(p2);
B(p2)=tmp;
F=[F;A;B];
[aa,bb]=size(F);
end
if aa>NP
F=F(1:NP,:); %保持种群规模为n
end
f=F; %更新种群
f(1,:)=R; %保留每代最优个体
clear F;
gen=gen+1
Rlength(gen)=minlen;
end
figure
for i=1:N-1
plot([C(R(i),1),C(R(i+1),1)],[C(R(i),2),C(R(i+1),2)],'bo-');
hold on;
end
plot([C(R(N),1),C(R(1),1)],[C(R(N),2),C(R(1),2)],'ro-');
title(['优化最短距离:',num2str(minlen)]);
figure
plot(Rlength)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
绘图函数
%连点画图函数 plot_route.m
function plot_route(a,R)
scatter(a(:,1),a(:,2),'rx');
hold on;
plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]);
hold on;
for i=2:length(R)
x0=a(R(i-1),1);
y0=a(R(i-1),2);
x1=a(R(i),1);
y1=a(R(i),2);
xx=[x0,x1];
yy=[y0,y1];
plot(xx,yy);
hold on;
end
end


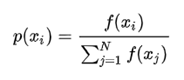
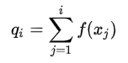
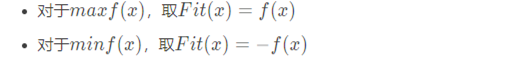


 浙公网安备 33010602011771号
浙公网安备 33010602011771号