【线性代数】正交矩阵和格兰姆-施密特正交化

引言

一组线性无关的向量可以张成一个向量子空间，比如向量\(\overrightarrow{e_1} = \left[ \begin{matrix} 1 \\ 2 \end{matrix} \right]\)和\(\overrightarrow{e_2} = \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]\)。它们线性无关，并且能张成一个二维平面。既然如此，那么为什么我们众所周知的二维坐标系是用\(\overrightarrow{i} = \left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]\)和\(\overrightarrow{j} = \left[ \begin{matrix} 0 \\ 1 \end{matrix} \right]\)表示，明明任意一组线性无关的2维向量都可以表示二维平面。这就引入了今天这篇笔记要讲的正交矩阵，得益于正交矩阵的性质，很多运算都可以被化简。

正交矩阵

之前的笔记中已经提到过正交向量，比如在\(R^n\)空间中两个n维向量\(\overrightarrow{e_1}、\overrightarrow{e_2}\)垂直，称这两个向量正交。而且显然，互为正交的一组向量(除去非零向量)必然线性无关，为此如果将一组n维正交向量放在一个矩阵中，比如$$A=
\begin{equation}
\left[
\begin{matrix}
e1 \ e2
\end{matrix}
\right]
\end{equation}

\[那么很显然，对于矩阵A，它有如下性质：\]

\begin{equation}
A^TA=\left[
\begin{matrix}
e1 \ e2
\end{matrix}
\right]\left[
\begin{matrix}
e1 \ e2
\end{matrix}
\right]=D
\end{equation}

\[矩阵$D$是一个对角矩阵，主对角线上的值分别对应着矩阵$A$中每一个列向量的模。那如果我们对矩阵A的要求更加严格一点，<font color=blue>要求矩阵$A$中每一个列向量都是单位向量</font>，那么对于新的矩阵A，它有如下性质：\]

\begin{equation}
A^TA=I
\end{equation}

\[矩阵$I$是2维单位矩阵，注意，这里的矩阵$A$并不方阵。<font color=blue>既然提到方阵，我们对矩阵$A$的要求更加严格一些，即要求它为方阵，我们记为$Q$</font>.对于$Q$： \]

\begin{equation}
\left {
\begin{array}{lr}
Q^TQ=I \
Q^T=Q
\end{array}
\right.
\end{equation}

\[我们称(4)中的矩阵$Q$为<font color=red>正交矩阵</font>。**它是一个方阵，并且列向量之间两两正交，每个列向量都是单位向量。** #### 正交矩阵举例 下面举几个正交矩阵的例子，\]

\left[
\begin{matrix}
1 & 0 \
0 & 1
\end{matrix}
\right]

\[又或者\]

\frac{1}{2}\left[
\begin{matrix}
1 & 1 & 1 & 1\
1 & -1 & 1 & -1\
1 & 1 & -1 & -1\
1 & -1 & -1 & 1
\end{matrix}
\right]

\[ ## 如何获得一个正交矩阵 因为一些原因，我们通常希望能够获得一个正交矩阵，但是很不巧，我们只有那个矩阵的"低级版本"，所有我们应该做些什么工作来获得一个正交矩阵。 将一个普通的方阵$A$转成正交矩阵，意味着要将$A$中的列向量变成线性无关的单位向量。所以主要流程就是两步：正交化和单位化 比较好用的一种办法是格兰姆-施密特正交化，下面以一个例子来演示它的流程。 ### 二维空间 先来个简单点的情况，假设有一个2x2的矩阵$$A= \left[ \begin{matrix} 3 & 2 \\ 4 & 1 \end{matrix} \right] \]

第一步：正交化

矩阵\(A\)中包含两个列向量，\(\overrightarrow{e_1} = \left[ \begin{matrix} 3 \\ 4 \end{matrix} \right]\)和\(\overrightarrow{e_2} = \left[ \begin{matrix} 2 \\ 1 \end{matrix} \right]\)

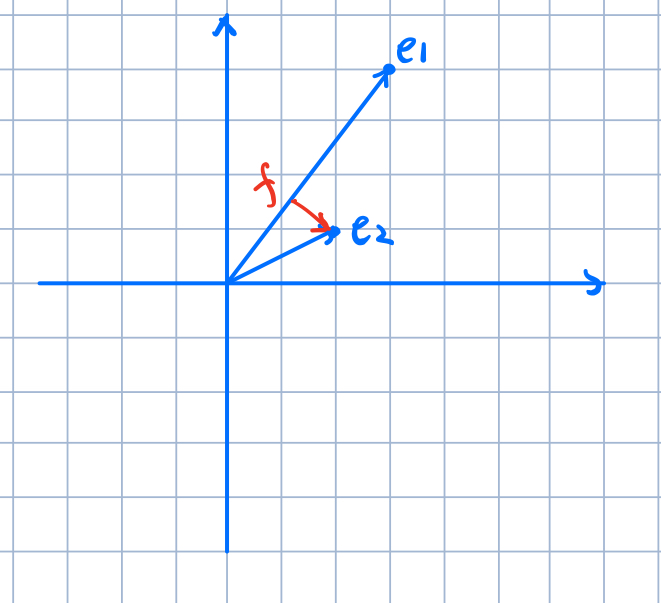
我们希望转化后的2个列向量正交，那么我可以从原来的2个列向量中先任取一个向量比如\(\overrightarrow{e_1} = \left[ \begin{matrix} 3 \\ 4 \end{matrix} \right]\)固定为\(\overrightarrow{q_1}\)，那么剩下的目标就是将另外一个向量\(\overrightarrow{e_2}\)转化为与\(\overrightarrow{q_2}\)，令它与\(\overrightarrow{q_1}\)正交。所以，我们先来写出正交化的第一步，即确定一个"固定"向量$$
\begin{equation}
\overrightarrow{q_1} = \overrightarrow{e_1}
\end{equation}

\[ 然后现在怎么得到一个$\overrightarrow{q_2}$？其实图上已经画出来了，如果将向量$\overrightarrow{e_2}$往向量$\overrightarrow{e_1}$投影先得到一个向量$\overrightarrow{f}$，那么向量$\overrightarrow{e_2} - \overrightarrow{f}$是不是显然与$\overrightarrow{e_1}$正交。那么第二步就是：\]

\begin{equation}
\overrightarrow{q_2} = \overrightarrow{e_2} - \overrightarrow{f},\ \ 其中\overrightarrow{f}为\overrightarrow{e_2}往\overrightarrow{q_1}的投影向量
\end{equation}

\[相信这个已经十分熟悉了，忘记的话可以回顾`如何得到一个投影矩阵`这篇笔记。\]

\begin{equation}
f = \frac{e_1^{{\mathrm{T}}e_2}{e_1}{\mathrm{T}}e_1}e_1
\end{equation}

\[由(6)、(7)可以确定向量$\overrightarrow{q_2}$：\]

\begin{equation}
q_2 = e_2 - \frac{q_1^{{\mathrm{T}}e_2}{q_1}{\mathrm{T}}q_1}q_1
\end{equation}

\[正交化到这里就结束了，我们代入例子算一下，得到变化后的矩阵为：\]

A' = \left[
\begin{matrix}
3 & \frac{4}{5} \
4 & \frac{-3}{5}
\end{matrix}
\right]

\[可以验证两个列向量是正交的了。 #### 第二步：单位化 这步就是将每个列向量的模变为1，拿$\overrightarrow{q_1} = \left[ \begin{matrix} 3 \\ 4 \end{matrix} \right]$举例，单位化后的向量为： \]

\frac{1}{\sqrt{3²⁺⁴2}}\left[
\begin{matrix} 3 \ 4
\end{matrix}
\right]=\left[
\begin{matrix} \frac{3}{5} \ \frac{4}{5}
\end{matrix}
\right]

\[而另一个向量$\overrightarrow{q_2}$已经是单位矩阵，所以不用单位化，因此通过格兰姆-施密特正交化最终得到的单位矩阵\]

Q = \left[
\begin{matrix}
\frac{3}{5} & \frac{4}{5} \
\frac{4}{5} & \frac{-3}{5}
\end{matrix}
\right]

\[ **正交化过程并不改变矩阵的对应的列空间，显然张成的平面仍是二维平面。** ### 三维空间 对于二维空间，确定1个固定的向量后，只要将另外一个向量往其上面投影再相减就能完成正交化过程了。但是在三维空间中，一共有3个列向量，应该怎么做？ #### 三维空间中的正交化过程 其实流程也是异曲同工。假设需要单位正交化的矩阵为$A = \left[ \begin{matrix} e_1 \ e_2 \ e_3 \end{matrix} \right]$ 1. 第一步：固定一个向量$q_1 = e_1$ 2. 第二步：将第2个向量往$q_1$上投影，$$q_2 = e_2 - \frac{q_1^{\mathrm{T}}e_2}{q_1^{\mathrm{T}}q_1}q_1\]

3. 第三步：将第3个向量\(e_3\)减去\(q_1\)方向上的投影向量，再减去\(q_2\)方向上的投影向量，即$$q_3=e_3 - \frac{q_1^{{\mathrm{T}}e_3}{q_1}{\mathrm{T}}q_1}q_1 - \frac{q_2^{{\mathrm{T}}e_3}{q_2}{\mathrm{T}}q_2}q_2$$

接下来单位化即可，不过多赘述。觉得第3步有些抽象的朋友可以找3只笔试一下，两只笔垂直放置在平面上，第3只笔与平面呈一定角度。这样减去两个方向的投影向量后，一定能得到垂直与平面的一个向量。而且也可以通过\(q_3^Tq_2=0\)和\(q_3^Tq_1=0\)来验证。