【排序】堆排序
什么是堆
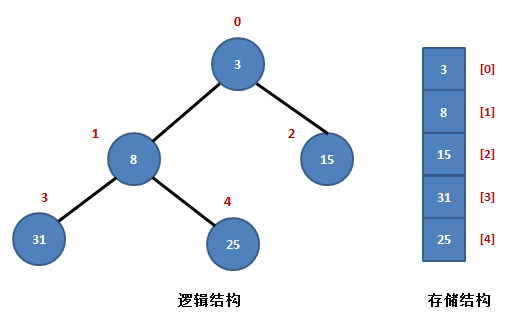
堆是一棵完全二叉树,可以用数组来存储。比如一个数组[3, 8, 15, 31, 24],具体为一个堆,它的逻辑结构如下所示:(图来自https://www.cnblogs.com/jingmoxukong/p/4303826.html#堆的概念,侵删)
 #### 最大堆和最小堆
#### 最大堆和最小堆
- 最大堆:根结点的值是所有堆结点值中最大者,且以每个节点为根的所有子堆都为最大堆。
- 最小堆:根结点的值是所有堆结点值中最小者,且以每个节点为根的所有子堆都为最小堆。
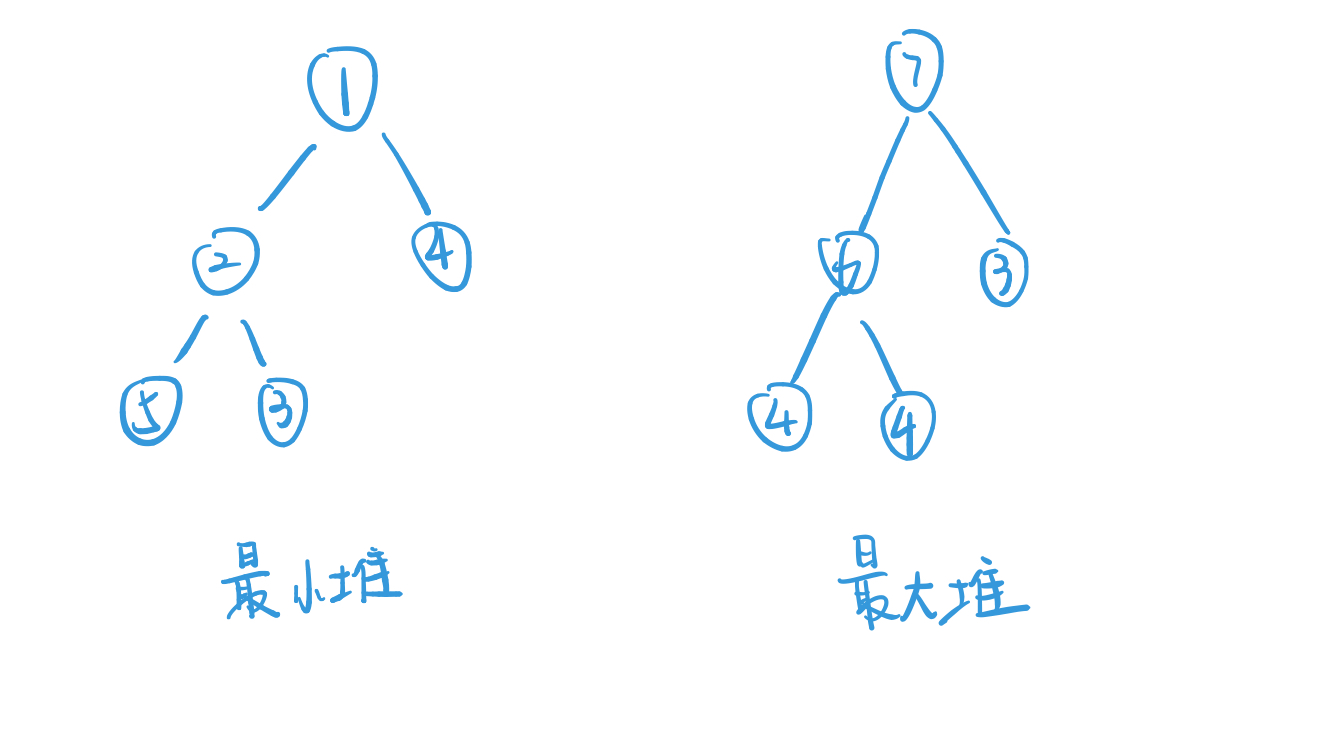
可以从图中发现最大堆/最小堆中,一个节点值的大小与它所在的深度无关,只与该节点的父节点有关。更简单说,对于最大堆,从某一个节点往下直到叶子节点,途中获得的值都在减少,比如[7, 6, 4].
堆的性质
由于堆在逻辑结构上实际为一棵完全二叉树,所以一个节点下标为p的两个子节点分别为:
- 2 * p + 1
- 2 * p + 2
如何将堆调整为最大堆
-
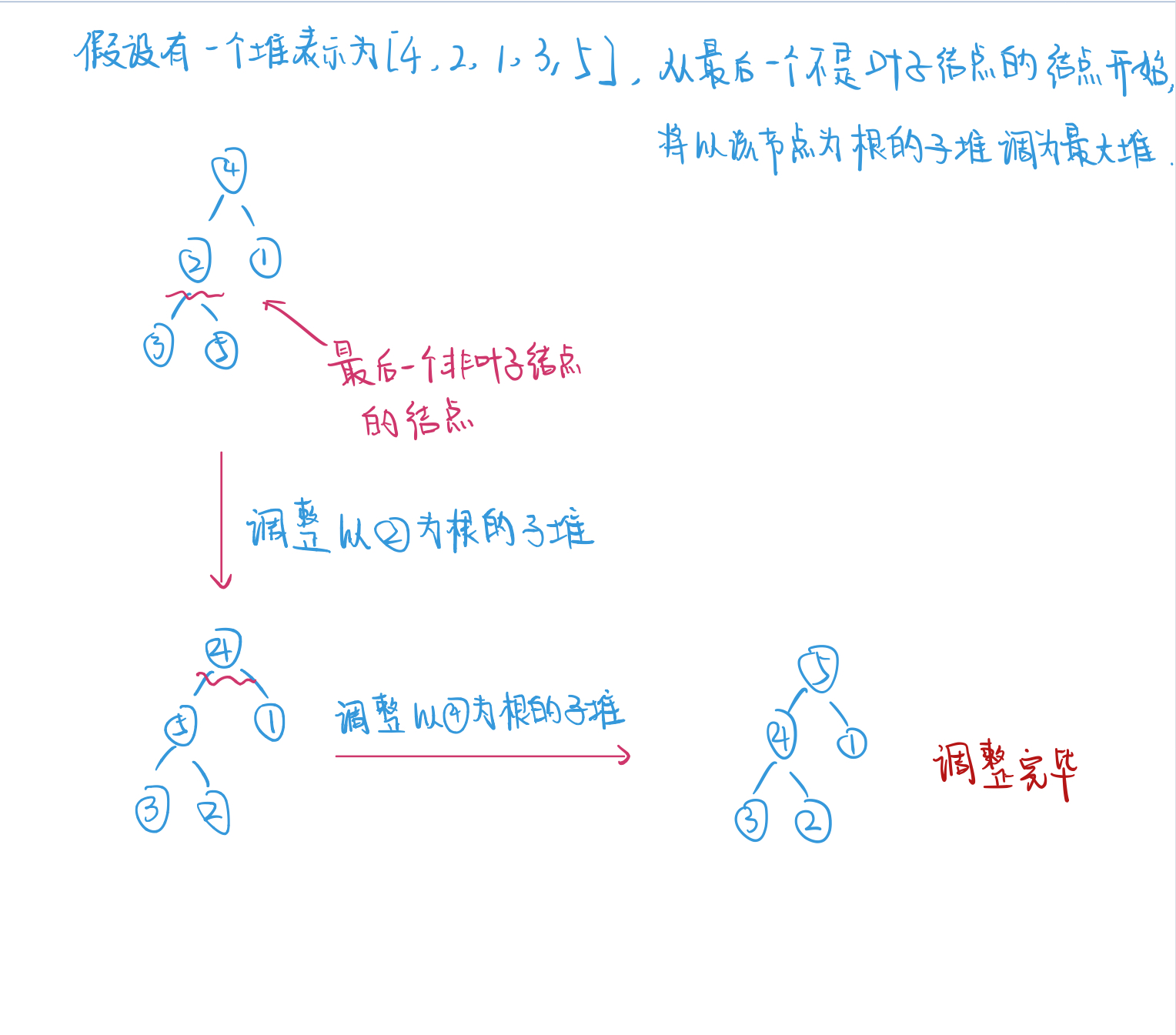
上面已经提到最大堆是长什么样子的了,下面给出调整最大堆的过程图:
-
用文字描述一下调整过程:
记堆的数据存放在一个数组nums中,N为数组的长度 1. 获取树中最后一个不是叶子节点的那个节点下标p 2. 开始循环 while p != 0: # PercDown是一个函数,用于调整以nums[p]为根的子堆到最大堆 PercDown(nums, p, N) p-- -
那么又有一个问题,
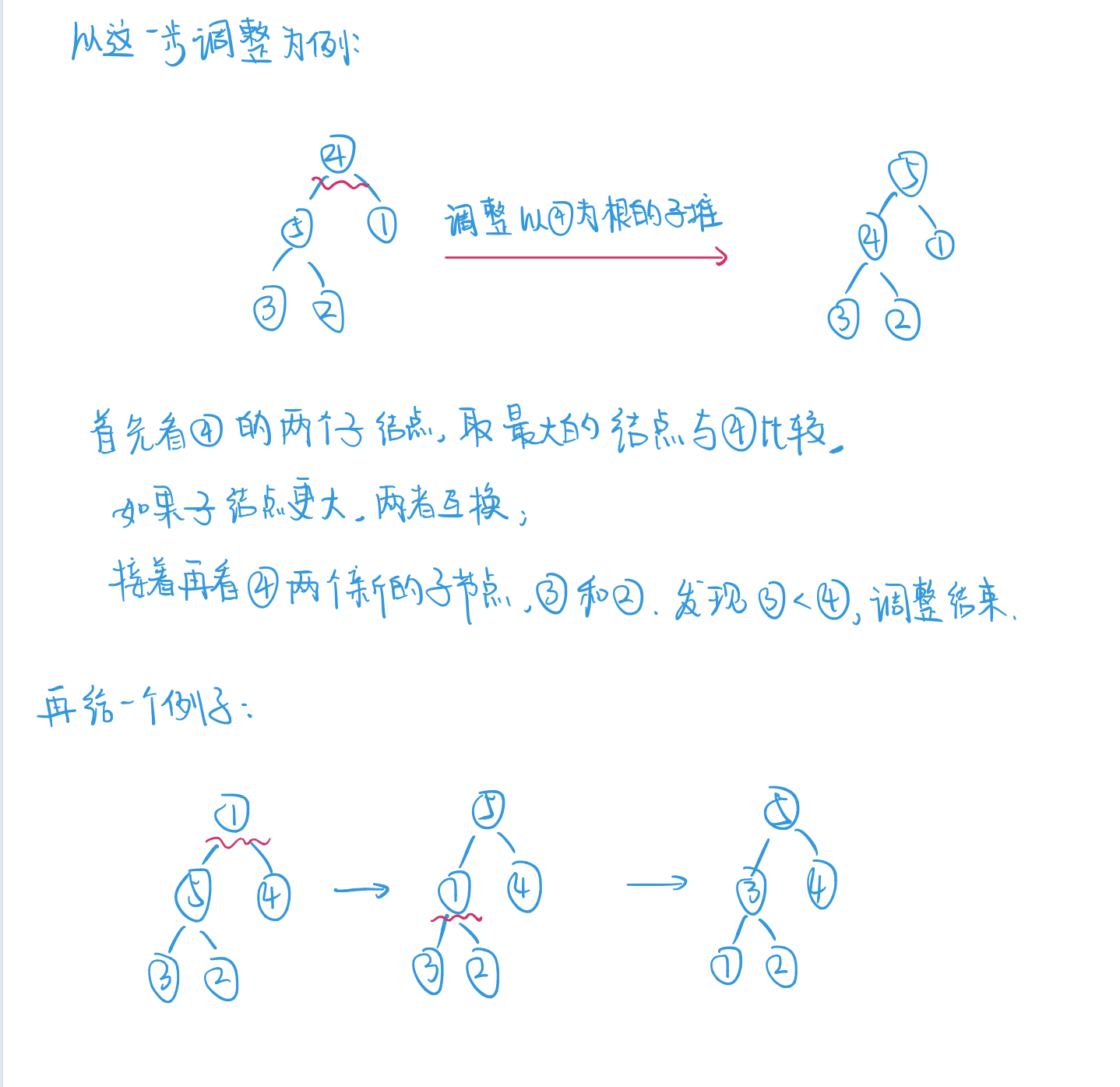
PercDown(nums, p, N)函数怎么工作的:
PercDown函数的代码
void PercDown( int A[], int p, int N )
{
/* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
int Parent, Child;
int X;
/* 取出根结点存放的值 */
X = A[p];
for (Parent = p; Parent*2+1 < N; Parent = Child) {
Child = Parent * 2 + 1; // 左节点下标
if( (Child!=N-1) && (A[Child]<A[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= A[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
A[Parent] = A[Child];
}
A[Parent] = X;
}
利用最大堆排序
那么已经调整好最大堆,怎么排序呢?聪明的办法是将nums[0]和nums最后一个数交换,然后将最大的那个数排除在nums外(可以用减少个数之类的办法),在利用PercDown调整以nums[0]为根的子堆将剩余的数重新调整为最大堆,还是上个图:

完整代码
#include <iostream>
using namespace std;
void Swap( int *a, int *b )
{
int t = *a;
*a = *b;
*b = t;
}
void PercDown( int nums[], int p, int N )
{
/* 将N个元素的数组中以nums[p]为根的子堆调整为最大堆 */
int Parent, Child;
int X;
/* 取出根结点存放的值 */
X = nums[p];
for (Parent = p; Parent*2+1 < N; Parent = Child) {
Child = Parent * 2 + 1;
if ((Child!=N-1) && (nums[Child] < nums[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
/* 找到了合适位置退出 */
if (X >= nums[Child])
break;
/* 下滤X */
else
nums[Parent] = nums[Child];
}
nums[Parent] = X;
}
void HeapSort(int nums[], int N)
{
/* 堆排序入口 */
int i;
/* 建立最大堆 */
for (i = N/2-1; i >= 0; i--)
PercDown(nums, i, N);
for (i=N-1; i>0; i--)
{
/* 删除最大堆顶 */
Swap(&nums[0], &nums[i]);
PercDown(nums, 0, i );
}
}
int main()
{
int nums[] = {4,3,1,2};
HeapSort(nums, 4);
for(int i : nums)
cout << i << ' ';
}




