146. LRU缓存机制
题目描述
运用你所掌握的数据结构,设计和实现一个LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
- 获取数据
get(key)- 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。 - 写入数据
put(key, value)- 如果密钥不存在,则写入其数据值。当缓存容量达到上限时,它应该在写入新数据之前删除最近最少使用的数据值,从而为新的数据值留出空间。
进阶:
你是否可以在 O(1) 时间复杂度内完成这两种操作?
示例:
LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4
算法
这题的时间复杂度的好坏比较依赖于所选择的数据结构。
LRU是操作系统中提出的一种应用于页置换的算法,这里不过多介绍,举个实际例子即可知道本题要求实现的功能需要什么步骤:
想象有一个队列的最大允许空间为3,
依次入队的顺序为 2,3,2,1,2,4;求LRU算法下队列的演变过程。
---------------------------------------------------
- 队列初始为空,2进入后队列情况为:2
- 队列还有2个剩余位置,3进入后队列情况为:2 3
- 队列还有1个剩余位置,这次入队的数据为2,它本来就已在队列中,根据LRU算法,需要将2调到队列末尾,因此队列情况为:3 2
- 队列还有1个剩余位置,这次入队数据为1,入队后队列情况为:2 3 1
- 队列已经没有剩余位置,但是入队数据为2,它本来就在队列中,根据LRU算法,需要将2调到队列末尾,因此队列情况为:3 1 2
- 队列已经没有剩余位置,新进入的数据为4,根据LRU需要淘汰最近最少被使用的数据,即队首的数据3,更新后队列情况为:1 2 4
---------------------------------------------------
上面即为LRU算法的一个例子
选择hash表与双向链表作为实现主体功能的两个数据结构,主要是因为双向链表便于插入删除,而hash表可以较快查找到需要返回的value。具体一点,整个LRUCache可能长下面这样:
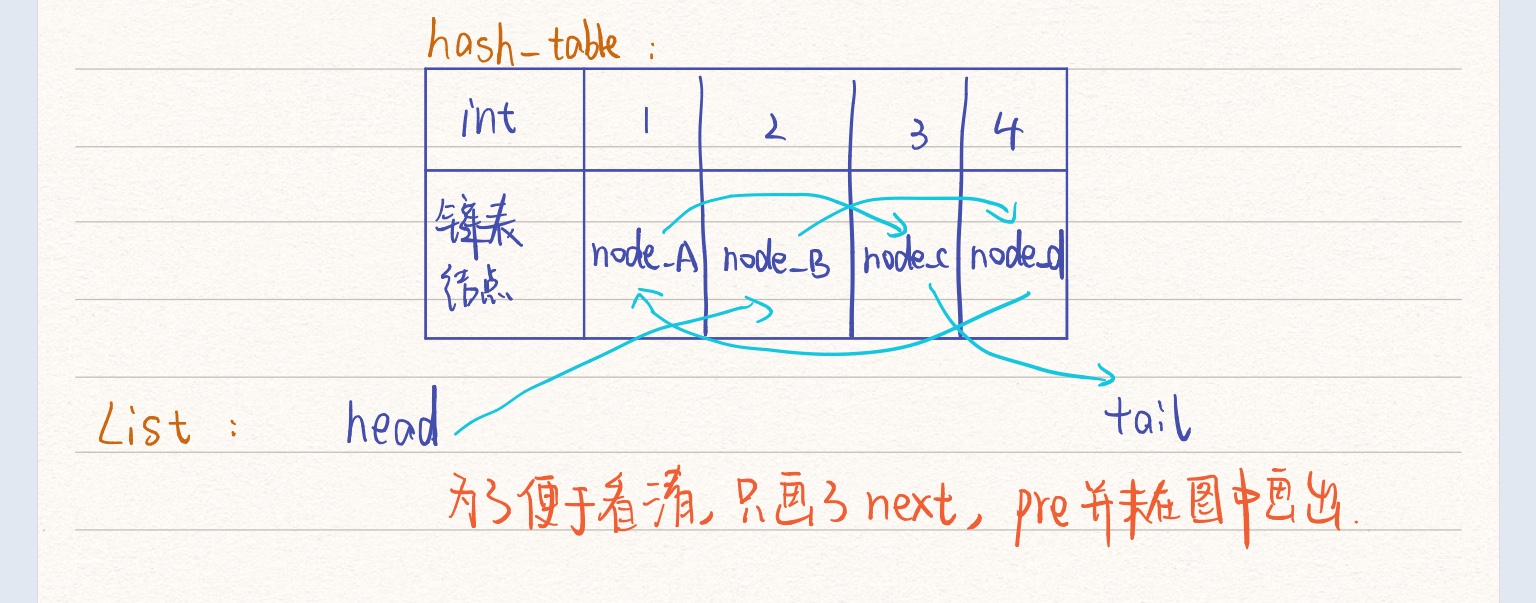
代码
#include <iostream>
#include <list>
#include <unordered_map>
using namespace std;
struct listNode{
int key, value;
listNode *pre, *next;
listNode(int _key, int _value): key(_key), value(_value)
{
pre = next = NULL;
}
};
class LRUCache {
public:
// hash_table末端保存最近刚被使用的节点,前端保存最近最少被使用节点
unordered_map<int, listNode*> hash_table;
listNode *head, *tail;
int cap, size;
LRUCache(int capacity) {
cap = capacity;
size = 0;
head = new listNode(-1, -1);
tail = new listNode(-1, -1);
head->next = tail;
tail->pre = head;
}
int get(int key) {
if (hash_table.find(key) == hash_table.end())
return -1;
else
{
// 记录该ID指向节点的指针
listNode *tmp = hash_table[key];
/*** 更改节点在表中的顺序 ***/
// 1. 删除hash_table[key]
delNode(tmp);
// 2. 将hash_table[key]插入末尾
pushNodeBack(tmp);
return tmp->value;
}
}
void put(int key, int value) {
// 这个key本身保存在表中
if (hash_table.find(key) != hash_table.end())
{
listNode *tmp = hash_table[key];
// 从链表头部去掉这个点
delNode(tmp);
// 更新表中key对应链表节点的value
tmp->value = value;
// 从链表尾部插入这个点
pushNodeBack(tmp);
return;
}
// 链表的空间已满
if (cap == size)
{
// 空间不够,踢出队列最前端的ID
listNode *tmp = head->next;
// 在表中删除这个点
hash_table.erase(tmp->key);
// 从链表头部去掉这个点
delNode(tmp);
// 释放被删除的点的空间
delete tmp;
}
else
size++;
listNode *node = new listNode(key, value);
hash_table[key] = node;
pushNodeBack(node);
}
void delNode(listNode *node)
{
node->pre->next = node->next;
node->next->pre = node->pre;
}
void pushNodeBack(listNode *node)
{
tail->pre->next = node;
node->pre = tail->pre;
node->next = tail;
tail->pre = node;
}
};
int main()
{
LRUCache *cache = new LRUCache(2);
cache->put(1, 1);
cache->put(2, 2);
cout << cache->get(1) << endl; // 返回 1
cache->put(3, 3); // 该操作会使得密钥 2 作废
cout << cache->get(2) << endl; // 返回 -1 (未找到)
cache->put(4, 4); // 该操作会使得密钥 1 作废
cout << cache->get(1) << endl; // 返回 -1
cout << cache->get(3) << endl; // 返回 3
cout << cache->get(4) << endl; // 返回 4
}




