带环链表 复杂链表 刷题+心得【C语言实现 】

1. 环形链表

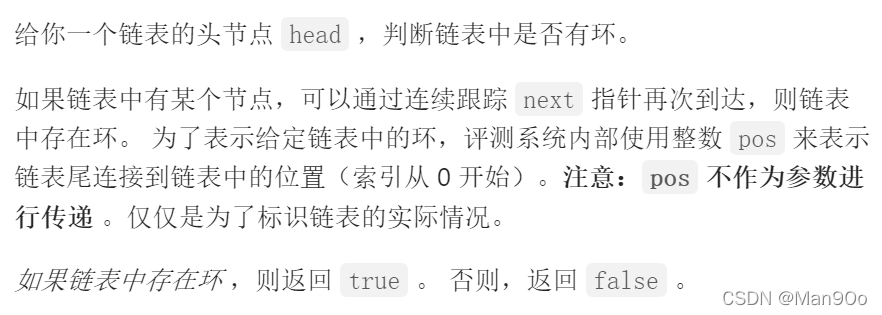
首先以此题作为链表带环问题的引入，首先给出此题的思路和代码

思路：

• 循环条件：fast和fast->next不能为NULL
• 注意：要先走一步再判断，因为fast和slow最初都指向head

bool hasCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;
    while(fast && fast->next)
    {
       
        fast = fast->next->next;
        slow = slow->next;
         if(slow == fast)
        {
            return true;
        }
    }
    return false;
}

链表带环问题

在解决带环问题时，我们使用了经典的快慢指针。但你有没有想过：

• 为什么fast走两步，slow走一步就能确定它有没有环呢？(这里仅讨论fast，理论上slow是一样的)
• 如果fast走3步，走n步，能否确定环一定存在呢？
• 怎样才能找到环的入口呢？(进入环的第一个节点)

下面给出证明：

fast2步，slow1步

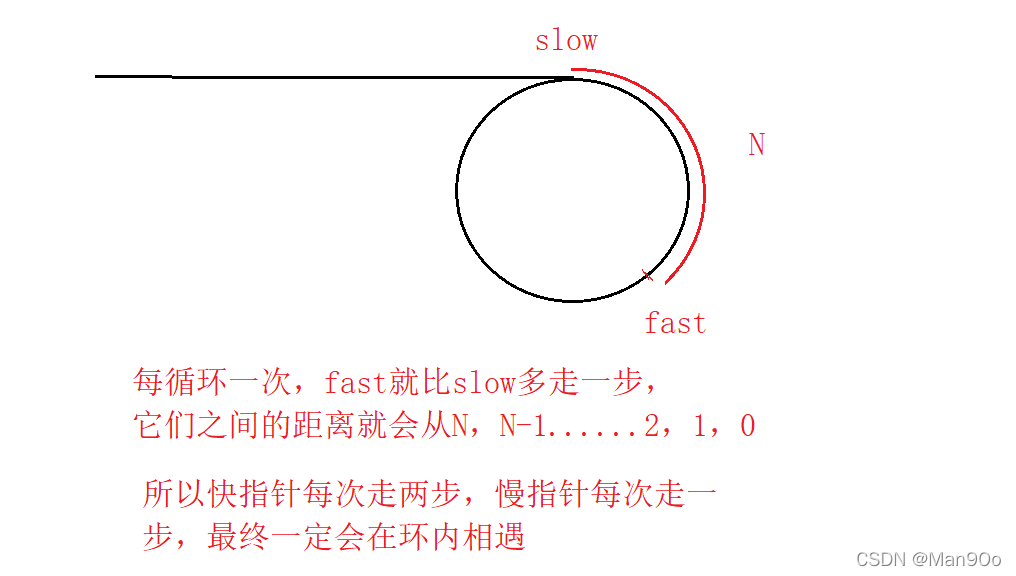
由上一题我们知道：如果链表带环，那么快慢指针一定会在环中相遇。这是判断链表带环与否的标志。下面假设链表有环。

在slow进环之前，fast一定已经进环。一旦slow进环(指向入口第一个节点)，fast和slow的关系就像追及问题，假设此时它们之间的距离为N。 这时候fast以每次比slow多一步的优势顺时针向slow进发。

fast3步，slow1步

顺着上面的思路：如果快指针每次走3步呢？快慢指针一定会在环内相遇吗？现在，fast以每次比slow多两步的优势顺时针向slow进发。

假设slow在入口时，它们之间的距离为奇数N每循环一次，它们的距离就会从N，N-2，… 1，-1(因为N是奇数)

这里的-1是什么意思呢？

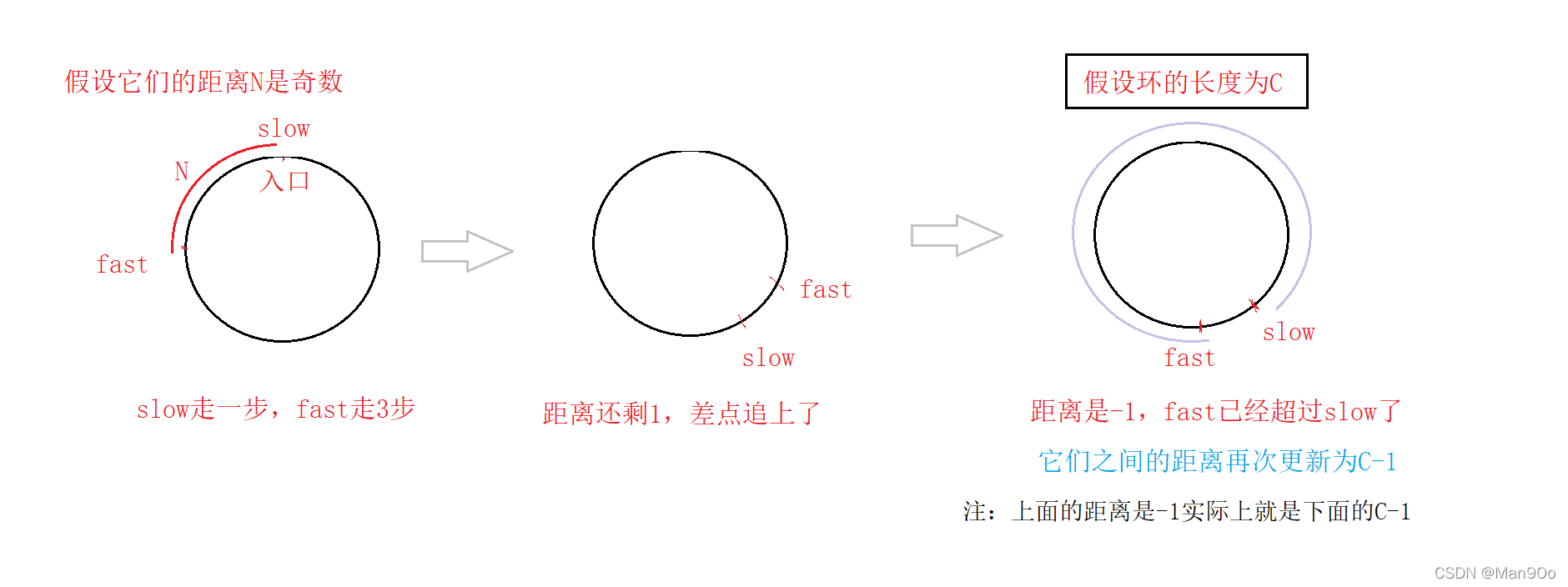
图中影响理解的关键点有：

1. 它们的起始距离N是奇数
2. fast比slow每次多走2步
3. 环的长度为C
4. 只要fast和slow不相等，这个循环就不会停止

看最后一个环中，如果环的长度是偶数，那么下轮循环开始时它们的距离C-1就是奇数，是不是会重蹈上面的覆辙？如此循环下去，slow和fast将永不相遇。

小结：在fast比slow每次多走2步的情况下，只要快慢指针之间的距离是奇数，那么随着循环的迭代，距离一定会再次减到-1，开启下一轮循环，永不相遇。其他情况也是类似的。

所以slow每次走1步，fast每次走3步，一定能确定链表带环吗？

不一定，得看起始时它们的距离和链表长度。

环的入口

假设起点到入口的距离为L，入口到相遇点的距离为X(顺时针)，环的长度为C

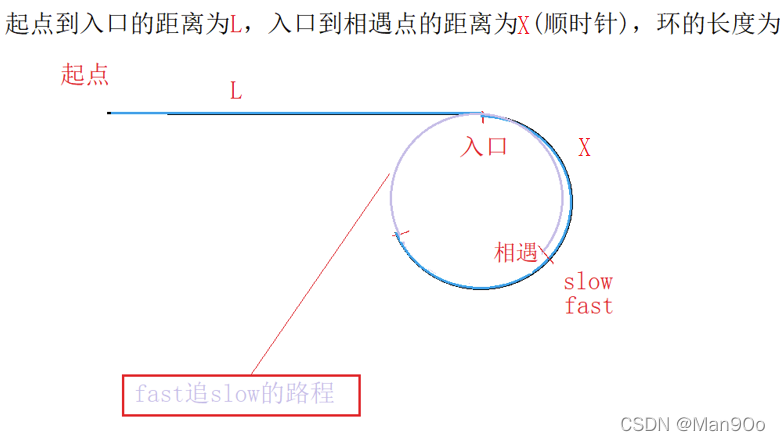
由以上的图示及快慢指针距离的倍数可以得出以下式子

单看式子比较抽象，把它放到环中看：

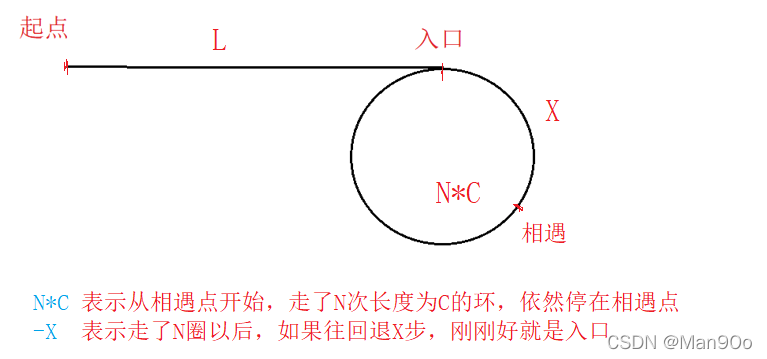
重新理解这个式子：左边直接锁定了入口(因为设L是起点和入口的距离)；右边可以理解为让指针从相遇点退回N圈，再退回X步。

即：一个指针从起点走，一个指针从相遇点走，如果有环，那么它们一定会在入口点相遇。

注：这里的往回退是想象地理解，实际上指针只能顺时针往下走。

2. 环形链表 II

思路：一个指针从起点走，一个指针从相遇点走，如果有环，那么它们一定会在入口点相遇。

先找到相遇点，然后让指针从相遇点和起点开始走，直到它们相等，即为入口。

• 循环终止条件：fast和slow相遇

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;
    struct ListNode * cur = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        //一个指针从起点走，一个指针从相遇点走，
        //那么它们一定会在入口点相遇
        if(fast == slow)
        {
            struct ListNode * meet = slow;//让meet从相遇点开始
            while(meet != cur)//让两个指针同时走
            {
                meet = meet->next;
                cur = cur->next;
            }
            if(meet == cur)
            {
                return meet;
            }
        }
    }
    return NULL;
}

3. 复制带随机指针的链表

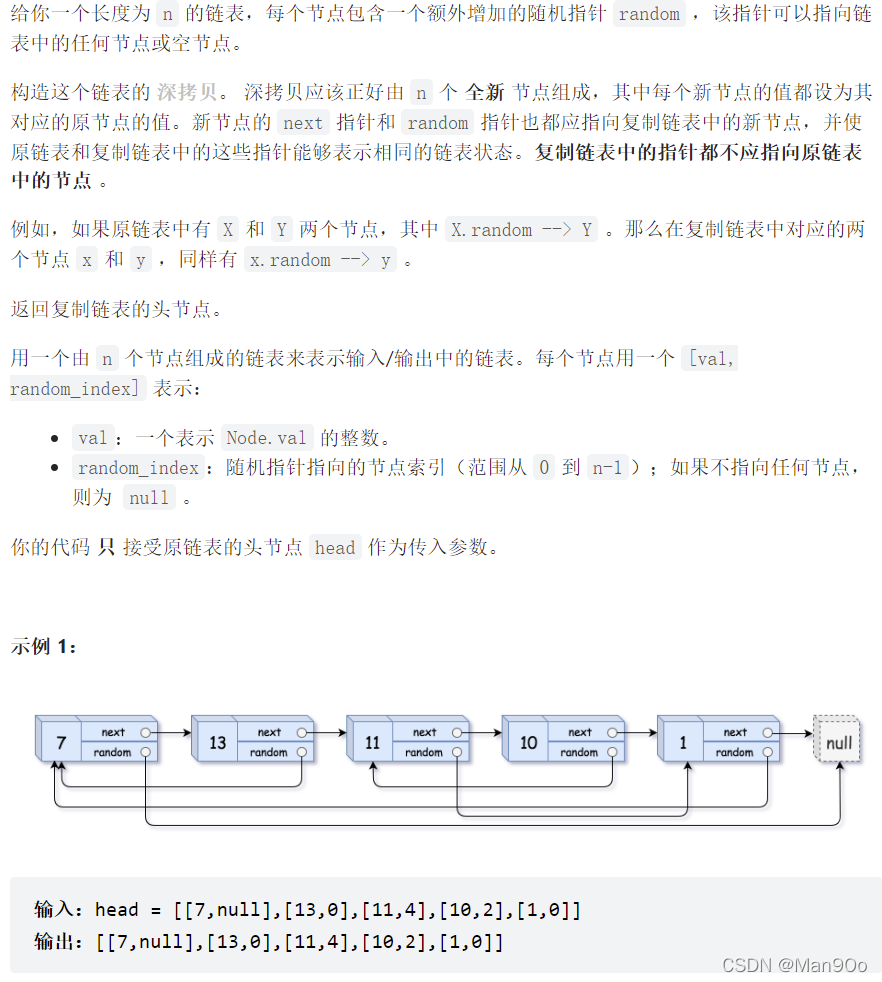
思路：
这道题表达得比较抽象，理解就ok了。

假如要复制一个普通的单向链表，只需复制数据，然后将所有节点按顺序链接即可。

而题目的意思是这个链表中除了有next这个指针变量，还有一个random指针变量，它的指向是指向任意节点的，如示例1。

那么复制它就不能像复制普通链表那样，单纯复制数据，然后链接。

思路1:

1. 遍历，先认为这是一个普通链表，只处理next和val，将它们链接起来，剩下每个节点的random；
2. 然后再遍历，处理random。但random指向的节点是随机的，而且val的值可能有多个节点，所以在处理每个random都要重新遍历一遍链表。

时间复杂度O(N*N)，效率不太高，虽然思路比较简单，但是实现起来复杂。

思路2:

1. 在每个原链表的每两个节点之间都插入一个新节点，这样处理random就好办了：想处理当前的新节点的random，只需找到它前一个节点(即当前位置的原节点)的random。新节点的random指向的地方就在原节点的random指向的下一个节点(要指向的新节点)
2. 把原链表连接回去
3. 把新链表连接上

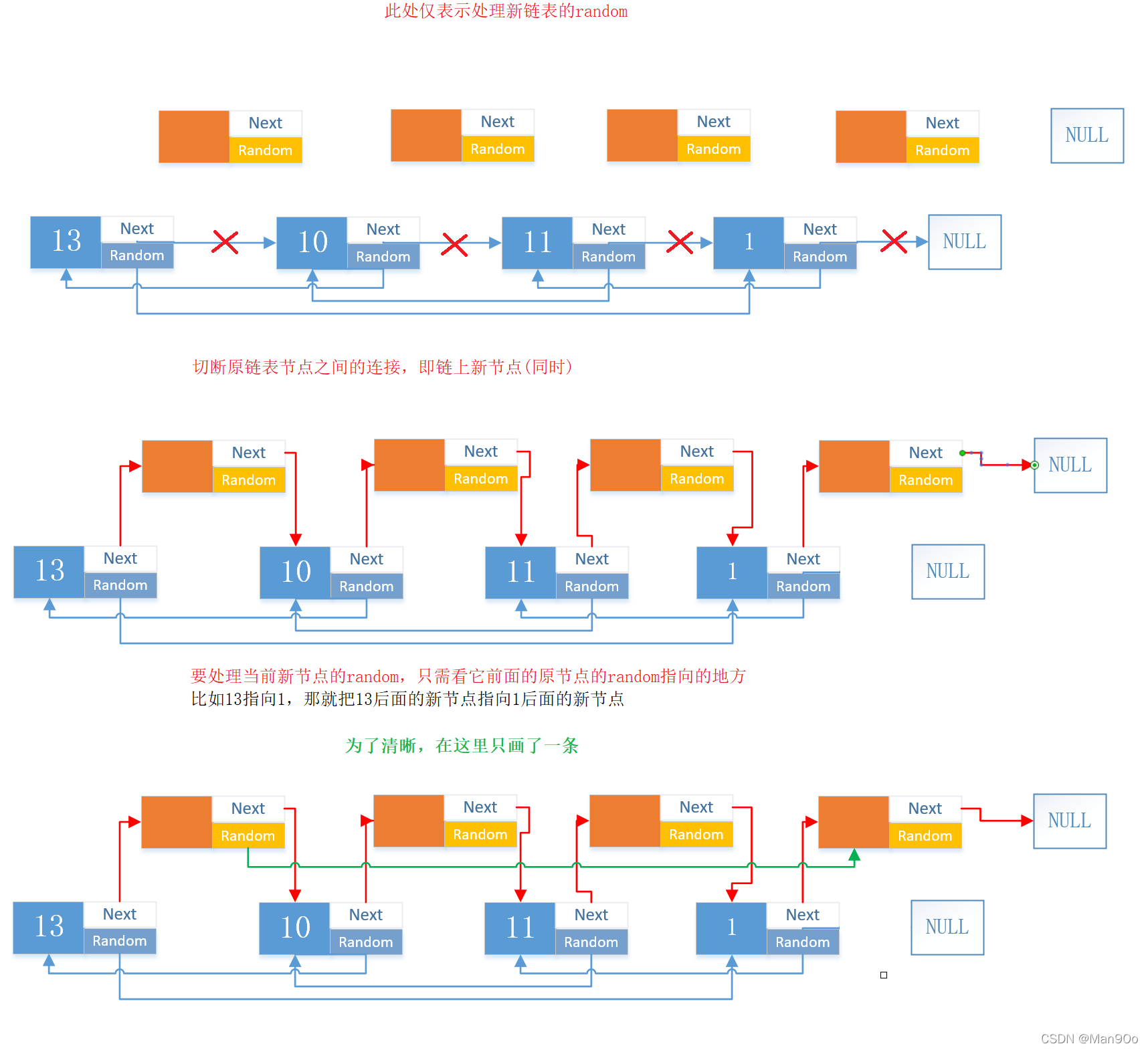
• 注意更新cur(cur是当前节点)
• 链接新链表的循环终止条件：cur遍历原链表为空时
• 注意判断head是否为空
• 先链，再处理random
• 最后再还原

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *next;
 *     struct Node *random;
 * };
 */

struct Node* copyRandomList(struct Node* head) {
    if(head == NULL)
        return head;
    struct Node* cur = head;
    while(cur)
    {
        struct Node* next = cur->next;
        struct Node* copy = (struct Node*)malloc(sizeof(struct Node));
        copy->val = cur->val;//拷贝val值
        cur->next = copy;//让旧指向新
        copy->next = next;//让新指向旧
        cur = next;//旧链表迭代
    }
    cur = head;//让cur重新回到起点
    //处理新random
    while(cur)
    {
        struct Node* copy = cur->next;//表示新节点在旧节点后面
        if(cur->random == NULL)//random可能没有指向
        {
            copy->random = NULL;
        }
        else
        {
            copy->random = cur->random->next;//将老random给新
        }
        cur = copy->next;//走两步才是下一个旧节点
    }
    //链接新链表，还原旧链表
    //其实就是删除节点，有三种情况：头尾中
    //顺便把删除的连接起来
    cur = head;//让cur重新回到起点
    struct Node* copyHead, *copyTail;
    copyHead = copyTail = (struct Node*)malloc(sizeof(struct Node));
    while(cur)
    {
        struct Node* copy = cur->next;//新
        struct Node* next = copy->next;//旧
        //新链表尾插
        copyTail->next = copy;
        copyTail = copyTail->next;
				//还原旧链表
        cur->next = next;
        cur = next;
        
    }
    struct Node* guard = copyHead;
    copyHead = copyHead->next;
    free(guard);
    return copyHead;
}

最后链接的部分：给新链表创建了一个头结点，最后要将返回的地址更新为头结点的下一个地址

4. 对链表进行插入排序

插入排序的核心思想(升序)：将数据分为两部分，前一部分看作是有序的，后半部分一个一个地跟前半部分的第一个比较，如果比它小，则放到它前面；否则跟它的下一位比较，如果要插入的数据比到最后还是比它大，则插入到前一部分的最后。

思路：

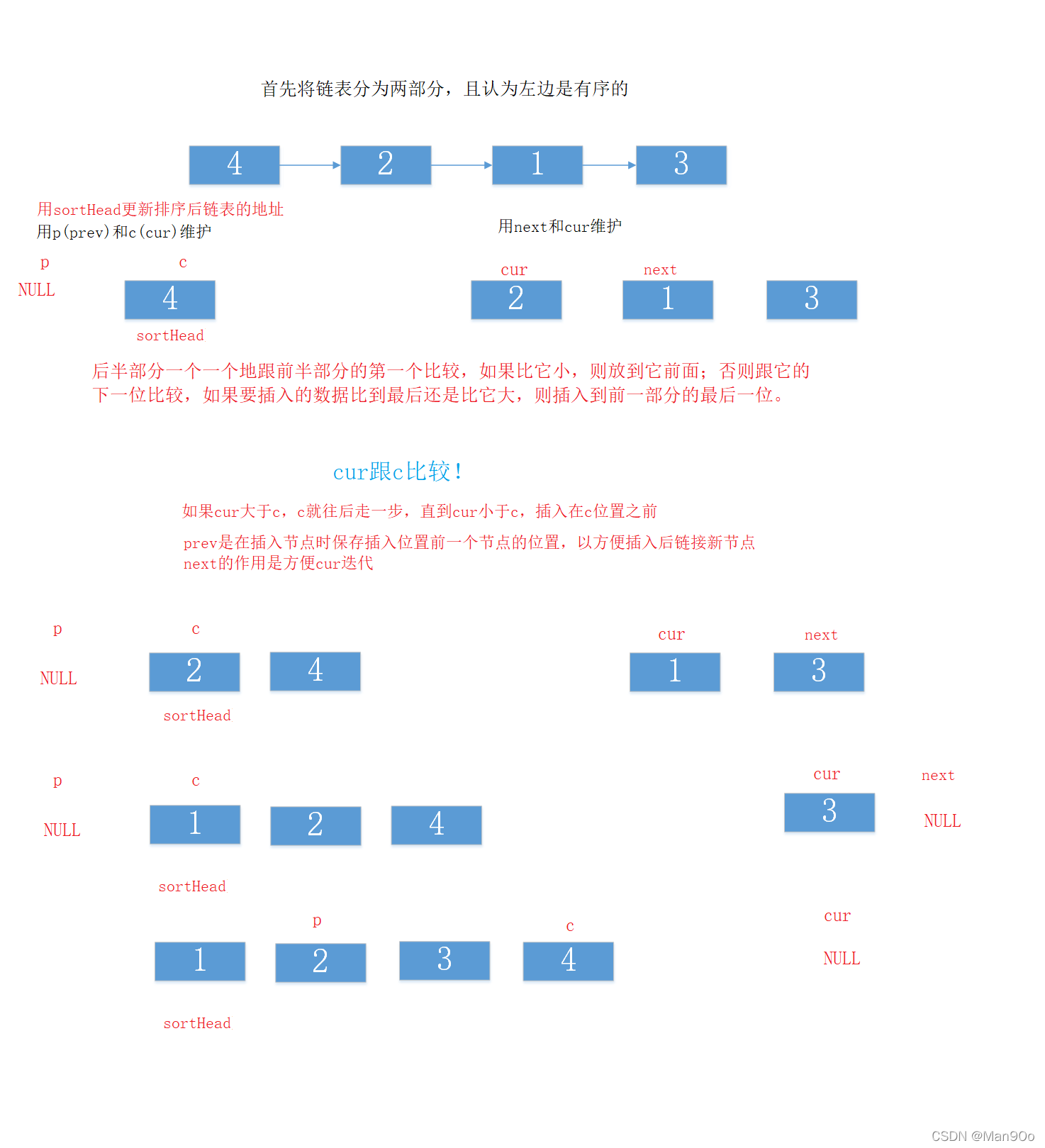
• 注意判断空链表和只有一个节点的情况

struct ListNode* insertionSortList(struct ListNode* head){
    if(head == NULL || head->next == NULL)//特殊情况
    {
        return head;
    }
    struct ListNode* sortHead = head;
    struct ListNode* cur = head->next;
    sortHead->next = NULL;
    //上面两句将链表分为两段
    while(cur)
    {
        struct ListNode* next = cur->next;//迭代条件
        struct ListNode* p = NULL;//这个p只有在插入时用来保存插入位置前一个节点的地址
        struct ListNode* c = sortHead;//更新排序后的链表的地址
        while(c)
        {
            if(cur->val < c->val)//符合插入条件，先跳过
            {
                break;
            }
            else//c往后移动
            {
                p = c;
                c = c->next;
            }
        }   
            if(p == NULL)//p是空，说明c一直是第一个，头插
            {
                cur->next = c;
                sortHead = cur;
            }
            else//p在中间
            {
                p->next = cur;
                cur->next = c;
            }
        cur = next;//迭代
    }
    return sortHead;
}

5. 删除有序链表中重复的元素-I

思路：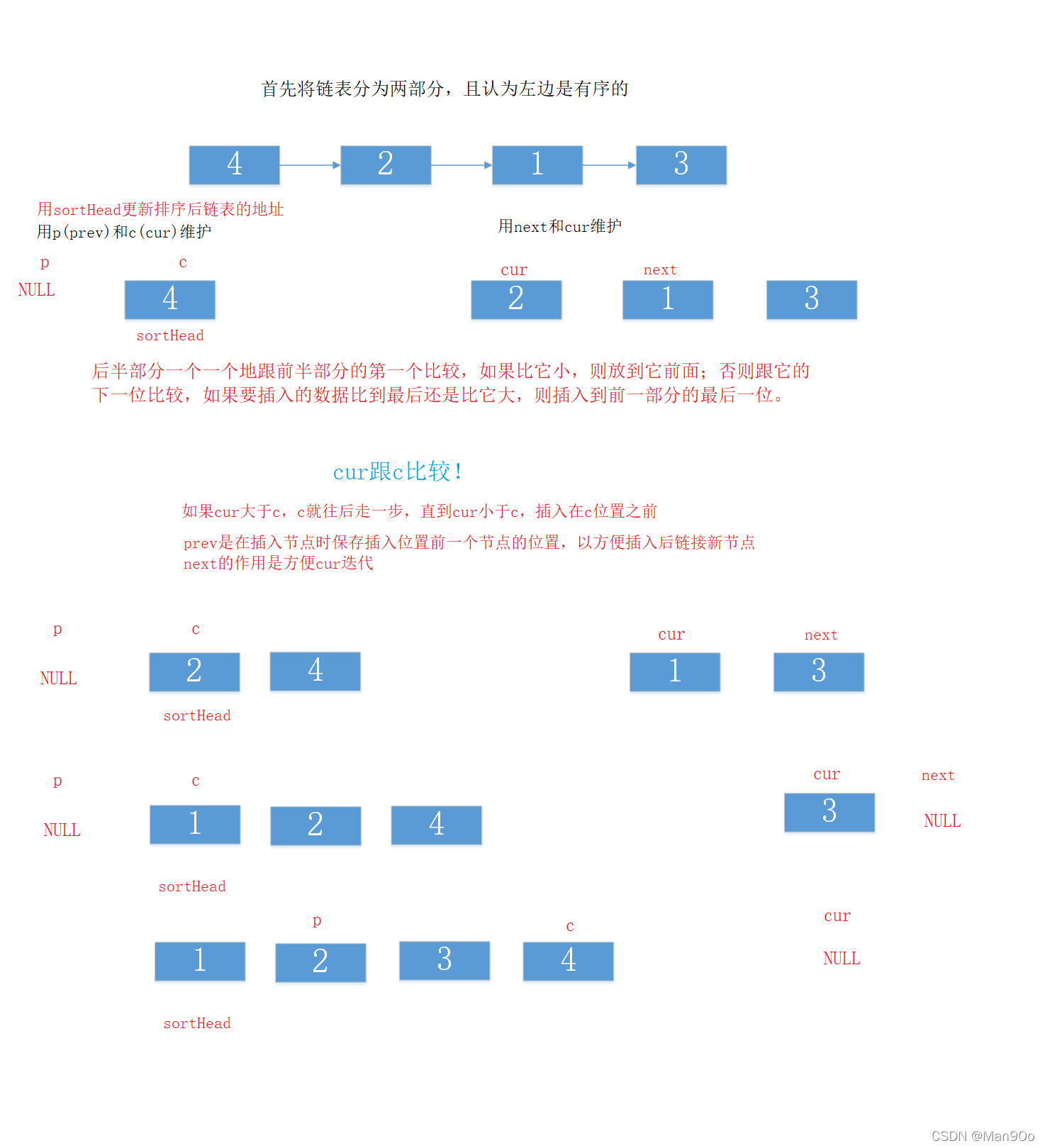

这是一个删除节点的问题，也是经典的快慢指针思想问题。即：如果指针所指节点val相同，快指针继续走，直到它们不相等，然后只保留一个，剩下的跳过。如此反复，直到快指针遍历完链表所有节点。

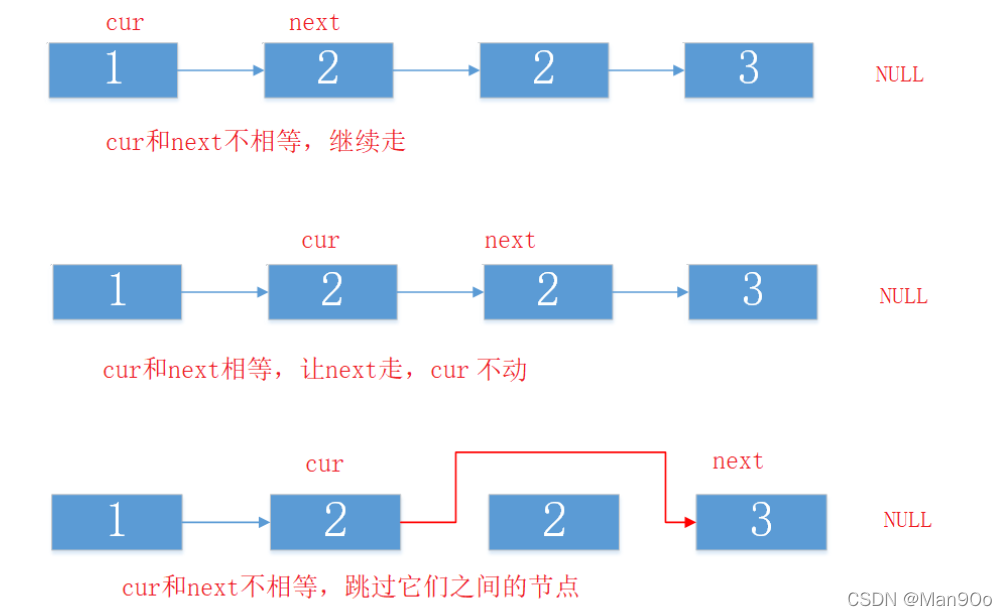
• 循环终止条件：next遍历完链表所有节点
• 注意判断链表是否为空和只有一个节点

struct ListNode* deleteDuplicates(struct ListNode* head ) {
    struct ListNode* cur = head;
    while(cur && cur->next)//cur判断链表为空的情况
    {
        if(cur->val == cur->next->val)//相等让next往下走
        {
            cur->next = cur->next->next;
        }
        else//否则让cur往前走
        {
            cur = cur->next;
        }
    }
    return head;
}

6. 删除有序链表中重复的元素-II

思路：

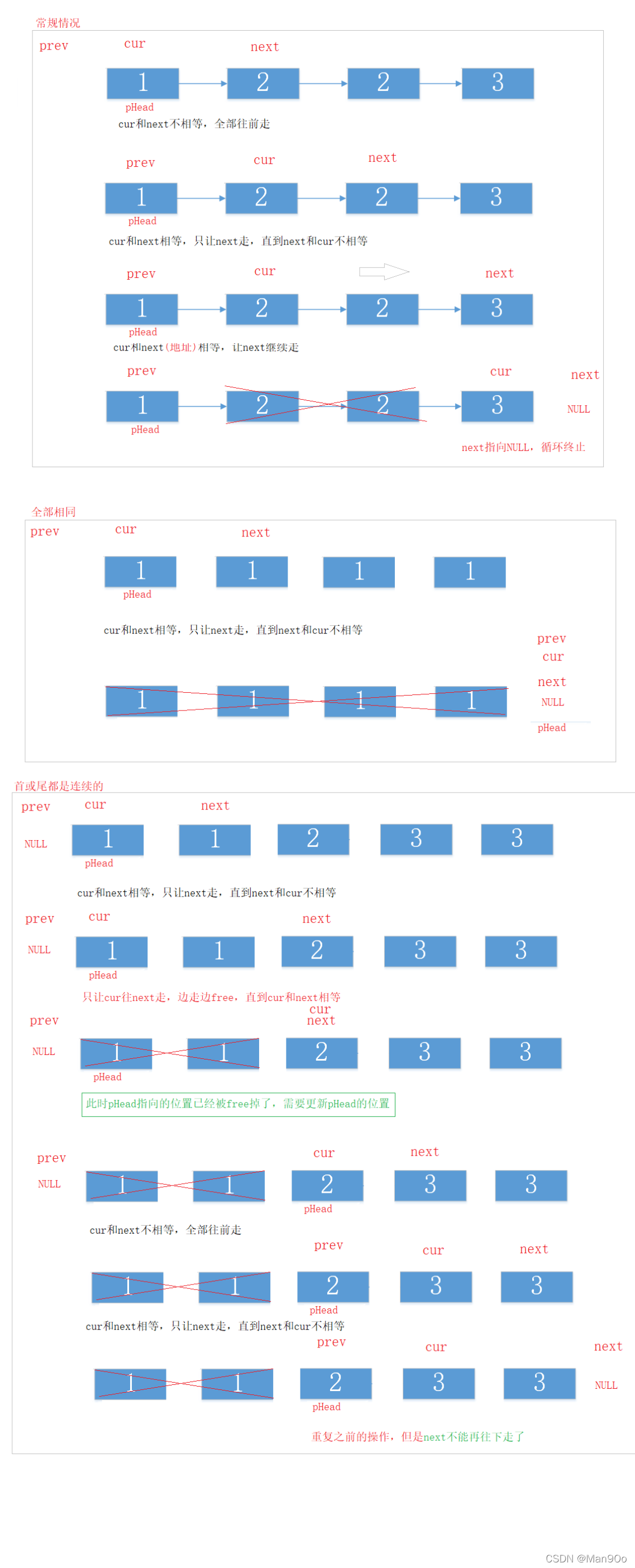
• 循环终止条件：next遍历完所有节点
• 注意判断链表为空和只有一个节点的情况
• 连续有首、中、尾、全这些情况。

struct ListNode* deleteDuplicates(struct ListNode* head ) {
    if(head == NULL || head->next == NULL)
        return head;
    struct ListNode* cur = head;
    struct ListNode* prev = NULL;
    struct ListNode* next = cur->next;
    while(next)
    {
        if(next->val == cur->val)
        {
            while(next && next->val == cur->val)//跳过相同的
            {
                next = next->next;//让next继续走
            }
            while(next != cur)//让cur到next的位置
            {
                struct ListNode* del = cur;
                cur = cur->next;
                free(del);//删除跳过的节点
            }
            if(prev == NULL)//prev空，是头部连续的标志
            {
                head = cur;//更新链表地址
            }
            else//不为空，说明prev在中间
            {
                prev->next = cur;//连接跳过之后的节点
            }
            if(next)//迭代
            {
                next = next->next;
            }
        }
        else//迭代
        {
            prev = cur;
            cur = next;
            next = next->next;
        }
    }
    
    return head;
}

心得

对链表的操作，无非就是增、删、改

增：头插、尾插、中间插

删：头删、尾删、中间删

• 对于单向链表，增或删都需要知道当前位置的上一个节点和下一个节点的信息。所以一般涉及删除或增加节点，都需要使用三指针分别维护当前位置的前一个节点，当前节点，下一个节点。通常分别用prev、cur、next命名
• 关于cur的迭代:当循环条件为cur不为空时,next不要写在while循环内,因为当cur为空时,next是野指针
• 画图是最最重要的，通过画图才能由清晰的思路。
• 通过画图得到的思路，不要立刻动手写代码，因为常常存在特殊情况。例如：链表为空或者只有一个，题目条件推出来的特殊情况，实在想不出其他情况了再动手写。然后看没有通过的用例来找到其他情况，调试代码。
• 有了较完整的思路还不够，将想法转换成代码的能力需要训练，实际上有不少地方是有差不多的“模板”的，例如：迭代next，要在循环的首尾处；多个指针同时迭代，从左往右修改等等。
• 涉及到对第一个节点的修改(单向无头不循环链表)，常常可以跳过添加一个哨兵位节点简化操作，在结束时再去掉它即可
• 调试的重要性:越界编译器不一定会报错.因为系统对越界的检查时设岗抽查,并不是在所有位置都检查是否越界,这与编译器和系统有关.所以我们要养成“防御式编程”的习惯

---

日志

4/18/2022

心得->关于第一个节点
4/19/2022

心得->cur的迭代、调试的重要性
man9o