联赛前第六阶段总结

总结 
总排名第5,较上次进步2名

这个阶段成绩上整体感觉良好，没有低级失分，状态不错

问题主要就是紧张度不够，听课改题效率有点低，下个阶段要注意一些了，时刻提醒自己

考试的时候时间安排还是有些不对劲，有的时候注意力也不集中，打完暴力就不想想题了。

还有建议数据造的好一点，别太毒瘤也别太水，
昨天白天的T4，我打了部分分，拿了60分，而去掉部分分，我就100分了，我明明算的后面70分的数据过不了
晚上的T1，要不是学长加了组数据，我暴力直接就A了，就算加了一组数据，我的暴力总时间都比正解短

晚间测试12

阶段排名 5

A Alyona and a tree

  • 老姚的数据真的是太棒辣！！！

  • 真就n方过百万，暴力碾标算呗（上面是我的，看运行时间）

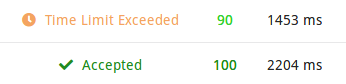
  • 考场上没想到倍增，然后就大法师了90分


B 跳房子 (Unaccepted)

  • 找了个循环节，时间复杂度压到nmq，拿了80分，最后实在没时间了，没时间卡常。



联赛模拟测试20

阶段排名 6

A Simple

  • 瞎搞出奇迹，成功骗到70分，水过了一道数学题。

  • 发现30分的暴力完全可以通过60分，剩下40%一定q>nm，打表发现答案为(m-1)(n-1)/2，然后就成功水过


B Walk

  • 30分暴力

  • 枚举边权值，每次只加边权是举值倍数的边，Dfs一遍，求最长链。

  • 看起来很不可过，但是跑过了


C Weed

  • 30分暴力

  • 和线段树维护单调栈类似，log的pushup


Drink (Unaccepted)

  • 30分暴力，还有30分部分分

  • 但是我如果不打30分部分分，我就直接A了...QWQ



晚间测试11

阶段排名 6

A 元素周期表

  • 借鉴凯尔的思路，从看题到切掉不到10分钟

B gcd (Unaccepted)

  • 搞了一个半小时最后看错题了，这个题目我真的是无fuck说，都没看见下标这两字就成下标了，郁闷极了，面对这样的题目描述，我只能说，%&%……%&×……×￥……%×&%￥&￥



联赛模拟测试19

阶段排名 7

A 建设城市

  • 一看就是数学题，推了半天没推出来啥有用的式子，就打了个暴搜，然后记忆化了一下，特判了一下，拿了60分

  • 容斥，答案=随便选-至少一个不满足的+至少两个不满足的-至少三个不满足的...

  • 至少i个不满足，就先把i×k个拿出来，剩下的放盒子里，然后再将拿出来的放回去，这样就是 C(n, i) * C(m - k * i - 1, n - 1)


B 军训队列

  • 写了个DP可惜不会斜率优化，就拿了50分

  • 正解没用斜率优化，考虑高度只有140.00~200.00，只有6000个数，去个重，开个氧气就过了

Show Code 
    for (int i = 1; i <= n; ++i)
        f[i] = (a[i] - a[1]) * (a[i] - a[1]);
    for (int l = 2; l <= k; ++l) {
        memcpy(g, f, sizeof(double) * (n + 1));
        for (int i = 1; i <= n; ++i) {
            f[i] = 1e9;
            for (int j = 1; j <= i; ++j)
                f[i] = std::min(f[i], g[j-1] + (a[i] - a[j]) * (a[i] - a[j]));
        }
    }

  • 写成这样就可以愉快的斜率优化了

  • 原式：

\[f_i=\min_{j=1}^i\{g_{j-1}+a_i^2-2a_ia_j+a_j^2\} \]

  • 换成\(y=ax+b\)形式：

\[g_{j-1}+a_j^2=2a_ia_j+f_i-a_i^2 \]

    for (int i = 1; i <= n; ++i)
        f[i] = (a[i] - a[1]) * (a[i] - a[1]);
    while (--k) {
        memcpy(g, f, sizeof(double) * (n + 1));
        int l = 1, r = 0;
        for (int i = 1; i <= n; ++i) {
            while (l < r && (g[i-1] + a[i] * a[i] - g[q[r]-1] - a[q[r]] * a[q[r]]) * (a[q[r]] - a[q[r-1]]) <= \
                    (g[q[r]-1] + a[q[r]] * a[q[r]] - g[q[r-1]-1] - a[q[r-1]] * a[q[r-1]]) * (a[i] - a[q[r]])) r--;
            q[++r] = i;
            while (l < r && g[q[l+1]-1] + a[q[l+1]] * a[q[l+1]] - g[q[l]-1] - a[q[l]] * a[q[l]] <= \
                    a[i] * 2 * (a[q[l+1]] - a[q[l]])) l++;
            f[i] = g[q[l]-1] + (a[i] - a[q[l]]) * (a[i] - a[q[l]]);
        }
    }

C 山屋惊魂 (Unaccepted)

  • 好好的大模拟非得弄个期望，只能把没有期望的那30分拿了，然后就弃了

D 彩球问题

  • 暴搜20分

  • 球是没有区别的，状态只需要还有几种球剩1个，剩2个，剩3个，以及上一次选的球剩了几个，状态只有121212*3，记忆化，然后高精度就行了

Bigint Dfs(int i, int j, int k, int x) {
    Bigint &s = f[i][j][k][x];
    if (!i && !j && !k) return s.b = 1, s;
    if (s.a || s.b) return s;
    if (i) s = s + Dfs(i - 1, j, k, 1) * (i - (x == 2));
    if (j) s = s + Dfs(i + 1, j - 1, k, 2) * (j - (x == 3));
    if (k) s = s + Dfs(i, j + 1, k - 1, 3) * k;
    return s;
}



联考day6

阶段排名 7

A 过河

  • 全场唯一正解，我真是高兴坏了，虽然我不会证明我那样写的正确性。

B 选数

  • 写了个\(O(2^nm^2)\)的，然后大力卡常，在register和抛弃了NOILinux的评测姬的帮助下跑过了1e9，拿了40分

  • 没看出来小r的改变其实就是把二进制数向左移了一位，然后把最高位移到最低位

  • 可以对操作前缀后缀异或和一下，在异或了i个数的时候小r改变一下就相当于前i次操作都左移了一位

  • 把m+1种可能的操作放在01trie上，每次向下递归，

  • 如果0和1都可以走，小r一定会让这一位的贡献为0，

  • 如果只有一个可以走，小s一定会让这一位做出贡献。

Code

Show Code 
#include <cstdio>

const int N = 1e5 + 5;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >= '0' &&  c <= '9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

int n, m, a[N], s1[N], s2[N], ans, cnt; 
int t[N<<5][2], trc;

void Add(int x) {
    int p = 0;
    for (int i = n - 1; i >= 0; --i) {
        bool y = x & (1 << i);
        if (!t[p][y]) t[p][y] = ++trc;
        p = t[p][y];
    }
}

void Dfs(int p, int s, int x) {
    if (!x--) {
        if (s > ans) ans = s, cnt = 1;
        else if (ans == s) cnt++;
        return;
    }
    if (t[p][0] && t[p][1])
        Dfs(t[p][0], s, x), Dfs(t[p][1], s, x);
    else Dfs(t[p][0] + t[p][1], s + (1 << x), x);
}

int main() {
    // freopen("choose.in", "r", stdin);
    // freopen("choose.out", "w", stdout);
    n = read(); m = read();
    for (int i = 1; i <= m; ++i)
        a[i] = read();
    for (int i = 1; i <= m; ++i)
        s1[i] = s1[i-1] ^ a[i];
    for (int i = m; i >= 1; --i)
        s2[i] = s2[i+1] ^ a[i];
    for (int i = 0; i <= m; ++i)
        Add((s1[i] * 2 / (1 << n) + s1[i] * 2) % (1 << n) ^ s2[i+1]);
    Dfs(0, 0, n);
    printf("%d\n%d\n", ans, cnt);
    return 0;
}

C 数列 (Unaccepted)

  • 又一道数学题，他们居然说纯暴搜40分，我直呼内行，我那12分暴搜才叫纯，啥情况都能枚举到

D 模板 (Unaccepted)

  • 看上去就像dsu，可惜我不会，最后1小时觉得70分可以用线段树合并写，但是由于太懒了，就去想T1了。



晚间测试10

阶段排名 6

A 分组 (Unaccepted)

  • 一眼不可做，瞎搞一通，拿了44。

B 大佬

  • 一眼期望题也不可做，本来打的8分的暴力，结果只拿了4分，可能是NOILinux太强了

  • 正解真是好简单，考虑每天期望值，然后乘上n-k+1天

  • 每天的就是i个数任意选的减去i-1个数任意选的，保证有i被选，然后乘上劳累度。

    for (int i = 1; i <= m; ++i)
        if ((ans += 1LL * (Pow(i, k) - Pow(i - 1, k) + M) * read() % M) >= M) ans -= M;
    printf("%lld\n", 1LL * ans * Pow(Pow(m, k), M - 2) % M * (n - k + 1) % M);



联考day5

阶段排名 3

遗忘之祭仪

  • 挺简单一题，把符卡能打的记录下来，每次扫到一个就消一遍，保证时间效率nm

  • 考场上没考虑符卡中没有x的情况，丢了10分


客星璀璨之夜

  • 一看期望，打了个30分暴力就Pass了

  • 只需要算出来每个距离被经过了多少次，然后用总距离/总方案数就是期望

  • 定义f[i][j]表示有i颗反物质行星，i+1颗正物质恒星，第j个间隔被经过的次数

  • 如果先选j之前的间隔，第j个间隔就成为了子问题的第j-2个间隔

  • 先选j之后的间隔，第j个间隔就成为了子问题的第j个间隔

  • 先选间隔j，第j个间隔就成为了子问题的第j-1个间隔，而且子问题的每个方案都至少有先选的这一次造成的贡献，

  • 转移方程：

\[f_{i,j}=(j-1)f_{i-1,j-2}+(2i-j)f_{i-1,j}+f_{i-1,j-1}+(i-1)!2^{(i-1)} \]


割海成路之日 (Unaccepted)

  • 觉得可以并查集做，搞了2小时样例都过不了，最后就剩6分钟了，一狠心就直接打包进去了，没想到还能拿35分。

posted @ 2020-10-18 12:00  Shawk  阅读(130)  评论(4)  编辑  收藏  举报