超级跳马 —— 矩阵快速幂优化DP
P3990 [SHOI2013]超级跳马
题目描述
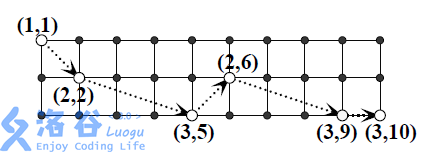
- 现有一个 n 行 m 列的棋盘，一只马欲从棋盘的左上角跳到右下角。每一步它向右跳奇数列，且跳到本行或相邻行。跳越期间，马不能离开棋盘。例如，当 n = 3, m = 10 时，下图是一种可行的跳法。
- 试求跳法种数mod 30011。
输入格式
- 仅有一行，包含两个正整数 n, m，表示棋盘的规模。
输出格式
- 仅有一行，包含一个整数，即跳法种数 mod 30011。
样例输入
3 5
样例输出
10
数据范围与提示
- 对于10%的数据，\(1 ≤ n ≤ 10,2 ≤ m ≤ 10\)；
- 对于50%的数据，\(1 ≤ n ≤ 10,2 ≤ m ≤ 10^5\)；
- 对于80%的数据，\(1 ≤ n ≤ 10,2 ≤ m ≤ 10^9\)；
- 对于100%的数据，\(1 ≤ n ≤ 502 ≤ m ≤ 10^9\)。
Solve
-
这题题意很清楚了，DP也很容易想到，\(f_{i,j}\) 表示到达第i列第j行的方案数，将起点方案数设为 1，每个点的方案数由可以过来的点转移，一看数据范围，n 就 50，m 最大 1e9 ，这几乎就可以想到是矩阵快速幂优化了，我们可以一步一步分析。
-
首先不难得出一个 \(O(n^3)\) 的写法。（20pts）
f[1][1] = 1; for (int i = 2; i <= m; ++i) for (int j = 1; j <= n; ++j) for (int k = i - 1; k >= 1; k -= 2) f[i][j] = (f[i][j] + f[k][j-1] + f[k][j] + f[k][j+1]) % M; -
注意到这只是求前面的和，限制条件也只有只能从奇数行转移，这样让 \(f_{i,j}\) 记录上奇数行的和就能优化到 \(O(n^2\)。（50pts）
-
这里的f数组要同时记录前缀和，所以最终答案是类似区间求和的形式：\(f_{m,n} - f_{m-2,n}\)
-
为了方便最后矩阵的写法，又因为他是由倒数第二行最后两列转移过来，就直接输出 \(f_{m-1,n}+f_{m-1,n-1}\)
f[1][1] = 1; for (int i = 2; i < m; ++i) for (int j = 1; j <= n; ++j) f[i][j] = (f[i-1][j] + f[i-1][j-1] + f[i-1][j+1] + f[i-2][j]) % M; printf("%d\n", (f[m-1][n] + f[m-1][n-1]) % M);
-
-
发现第 i 列只由第 i-1 列和 i-2 列转移过来的，而且列数又那么大，考虑矩阵快速幂优化：
- 可以类比斐波那契数列的写法，将 \(f_{i.k}\)和\(f_{i-1,k}(k\in {1,...,n})\)的状态压成一个 \(1\times 2n\) 的矩阵，乘上一个转移矩阵，得到 \(f_{i+1.k}\)和\(f_{i,k}(k\in {1,...,n})\)的状态，转移矩阵根据上面第二个解法的转移方程构造，还是举 n=4 的例子
\[\begin{bmatrix}
f_{i,1} & f_{i,2} &f_{i,3} &f_{i,4} &f_{i-1,1} &f_{i-1,2} &f_{i-1,3} &f_{i-1,4}
\end{bmatrix}
\ast
\begin{bmatrix}
1 & 1 & 0& 0 & 1& 0 &0 & 0\\
1& 1& 1 & 0& 0 &1 & 0 &0 \\
0 & 1 & 1& 1& 0 & 0 & 1 & 0\\
0 & 0 & 1 & 1 &0 & 0 & 0 &1 \\
1 & 0 &0 & 0 & 0 &0 & 0 &0 \\
0& 1 & 0& 0& 0& 0& 0& 0\\
0& 0& 1& 0& 0 & 0&0&0 \\
0& 0 & 0& 1 & 0 & 0 & 0 & 0
\end{bmatrix}
=
\begin{bmatrix}
f_{i+1,1} & f_{i+1,2} &f_{i+1,3} &f_{i+1,4} &f_{i,1} &f_{i,2} &f_{i,3} &f_{i,4}
\end{bmatrix}\]
这个式子有亿点长啊
转移矩阵：
\[\begin{bmatrix}
1 & 1 & 0& 0 & 1& 0 &0 & 0\\
1& 1& 1 & 0& 0 &1 & 0 &0 \\
0 & 1 & 1& 1& 0 & 0 & 1 & 0\\
0 & 0 & 1 & 1 &0 & 0 & 0 &1 \\
1 & 0 &0 & 0 & 0 &0 & 0 &0 \\
0& 1 & 0& 0& 0& 0& 0& 0\\
0& 0& 1& 0& 0 & 0&0&0 \\
0& 0 & 0& 1 & 0 & 0 & 0 & 0
\end{bmatrix}\]
初始矩阵
\[\begin{bmatrix}
1 & 1 & 0 & 0 & 1 & 0 & 0 & 0
\end{bmatrix}\]
- 需要注意的几点：
- 因为矩阵无法处理 \(m\le 2\) 的情况，所以需要特判。只有 \(f_{1,1},f_{1,2},f_{2,2}\)值为1,其他情况都是0.
- 此解法只处理了 \(n>1\) 的情况，对于 \(n=1\) 的情况打表发现可以转换成斐波那契数列，而且此时转移矩阵与求斐波那契数列的转移矩阵也很想，也特判一下就好了。
- 接下来就是实现，具体看代码。
Code
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 105, M = 30011;
int n, n2, m;
struct Matrix {
int a[N][N];
Matrix () {
memset(a, 0, sizeof(a));
}
int *operator [] (const int &i) {
return a[i];
}//重载方括号运算符，写起来方便
Matrix operator * (const Matrix &b) {
Matrix c;
for (int i = 1; i <= n2; ++i)
for (int j = 1; j <= n2; ++j)
for (int k = 1; k <= n2; ++k)
(c.a[i][j] += a[i][k] * b.a[k][j] % M) %= M;
return c;
}//重载乘号
void Print() {
for (int i = 1; i <= n2; ++i, puts(""))
for (int j = 1; j <= n2; ++j)
printf("%d ", a[i][j]);
puts("");
}//调试输出用
}a, b, c;
Matrix Pow(Matrix a, int k) {
Matrix ans = a; k--;
for (; k; k >>= 1, a = a * a)
if (k & 1) ans = ans * a;
return ans;
}//快速幂
int main() {
scanf("%d%d", &n, &m);
if (m <= 2) {
if (n <= 2 && m <= n) puts("1");
else puts("0");
return 0;
}//特判情况1
n2 = n << 1;
for (int i = 1; i <= n; ++i) {//构造转移矩阵
a[i][i-1] = a[i][i] = a[i][i+n] = a[i+n][i] = 1;
if (i != n) a[i][i+1] = 1;
}
b = Pow(a, m - 2);
if (n == 1) return printf("%d\n", b[1][1]), 0;//特判情况2
int s1 = (b[1][n2-1] + b[2][n2-1] + b[n+1][n2-1]) % M;
int s2 = (b[1][n2] + b[2][n2] + b[n+1][n2]) % M;
//根据初始矩阵和快速幂后的转移矩阵求得目标矩阵的有用值
printf("%d\n", (s1 + s2) % M);
//s1是f[m-1][n-1]，s2是f[m-1][n]，加起来就是答案
return 0;
}
