20200722水题大战Vol.2 题解
A. T1(天际线)
题目描述
- Latium省的Genoa是亚平宁半岛西海岸北端的一片土地,自然资源丰富,却无人居住。你受到罗马执政官Caesar的委任,前往Genoa建立新的城市。Caesar对这次任务的要求是在Genoa这片土地上建立起一座繁荣的城市,他将以此作为衡量你的表现的标准。
- 正在你大刀阔斧地进行城市建设的时候,Caesar突然写信给你,说他要检查Genoa的建设情况。Caesar希望知道你的城市是什么样子,但是他又非常的忙,所以他只要你描述一下城市的轮廓就可以了,他将依照城市的轮廓决定你的薪水。
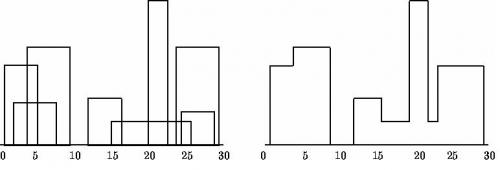
- 怎样描述一个城市的轮廓呢?我们知道Genoa所有的建筑共享一个地面,你可以认为它是水平的。所有的建筑用一个三元组(Li,Hi,Ri)其中Li和Ri分别是建筑的左坐标和右坐标,Hi就是建筑的高度。在下方所示的图表中左边建筑物描述如下(1,11,5),(2,6,7),(3,13,9),(12,7,16),(14,3,25),(19,18,22),(23,13,29),(24,4,28),右边用轮廓线的顺序(1,11,3,13,9,0,12,7,16,3,19,18,22,3,23,13,29,0)表示:
输入格式
- 在输入数据中,你将得到一系列表示建筑的三元组。在输入数据中所有建筑的坐标中的数值都是小于10000的正整数,且至少有1幢建筑,最多有5,000幢建筑。在输入输入中每幢建筑的三元组各占一行。三元组中的所有整数应由一个或多个空格分开。
输出格式
- 在输出数据中,你被要求给出城市的轮廓线。你可以这样来描述:对于所有轮廓线上的折点,按顺序排好,第奇数个点输出x坐标,第偶数个点输出y坐标,两个数之间用空格分开。
样例输入
1 11 5
2 6 7
3 13 9
12 7 16
14 3 25
19 18 22
23 13 29
24 4 28
样例输出
1 11 3 13 9 0 12 7 16 3 19 18 22 3 23 13 29 0
Solve
- 标记永久化+动态开点线段树维护区间最大值
- 题目要求输出折点,其实就是左闭右开修改,最后遍历一边,输出最大值与左面不同的点的位置
Code
#include <cstdio>
#include <algorithm>
#define tree 1, 1, 1e5
#define lson rt << 1, l, mid
#define rson rt << 1 | 1, mid + 1, r
using namespace std;
const int N = 1e5 + 5;
int a[N], t[N<<2], x, y, h;
void Change(int rt, int l, int r) {
if (x > r || y < l) return;
if (x <= l && r <= y)
return t[rt] = max(t[rt], h), void();
int mid = l+r >> 1;
Change(lson); Change(rson);
}
void Ask(int rt, int l, int r, int m) {//m沿途收集最大值标记
if (l == r) return a[l] = max(m, t[rt]), void();
int mid = l+r >> 1;
Ask(lson, max(m, t[rt]));
Ask(rson, max(m, t[rt]));
}
int main() {
while (scanf("%d%d%d", &x, &h, &y) == 3)
y--, Change(tree);
Ask(tree, t[1]);
for (int i = 1; i <= 1e5; ++i)
if (a[i] != a[i-1])
printf("%d %d\n", i, a[i]);//luogu上不用输出\n
return 0;
}
B. T2(免费道路)
题目描述
- 新亚(New Asia)王国有 N 个村庄,由 M 条道路连接。其中一些道路是鹅卵石路,而其它道路是水泥路。保持道路免费运行需要一大笔费用,并且看上去 王国不可能保持所有道路免费。为此亟待制定一个新的道路维护计划。
- 国王已决定保持尽可能少的道路免费,但是两个不同的村庄之间都应该一条且仅由一条 且仅由一条免费道路的路径连接。同时,虽然水泥路更适合现代交通的需 要,但国王也认为走在鹅卵石路上是一件有趣的事情。所以,国王决定保持刚好 K 条鹅卵石路免费。
- 举例来说,假定新亚王国的村庄和道路如图 3(a)所示。如果国王希望保持两 条鹅卵石路免费,那么可以如图 3(b)中那样保持道路(1, 2)、(2, 3)、(3, 4)和(3, 5) 免费。该方案满足了国王的要求,因为:(1)两个村庄之间都有一条由免费道 路组成的路径;(2)免费的道路已尽可能少;(3)方案中刚好有两条鹅卵石道路 (2, 3)和(3, 4)

- 图 3: (a)新亚王国中村庄和道路的一个示例。实线标注的是水泥路,虚线标注 的是鹅卵石路。(b)一个保持两条鹅卵石路免费的维护方案。图中仅标出了免费道路。
- 给定一个关于新亚王国村庄和道路的述以及国王决定保持免费的鹅卵石道路数目,写一个程序确定是否存在一个道路维护计划以满足国王的要求,如果 存在则任意输出一个方案。
输入格式
- 输入第一行包含三个由空格隔开的整数:
- N,村庄的数目(1≤N≤20,000);
- M,道路的数目(1≤M≤100,000);
- K,国王希望保持免费的鹅卵石道路数目(0≤K≤N - 1)。
- 此后 M 行述了新亚王国的道路,编号分别为 1 到 M。第(i+1)行述了第 i 条 道路的情况。用 3 个由空格隔开的整数述:
- ui 和 vi,为第 i 条道路连接的两个村庄的编号,村庄编号为 1 到 N;
- ci,表示第 i 条道路的类型。ci = 0 表示第 i 条道路是鹅卵石路,ci = 1 表 示第 i 条道路是水泥路。
- 输入数据保证一对村庄之间至多有一条道路连接
输出格式
- 如果满足国王要求的道路维护方案不存在,你的程序应该在输出第一行打印 no solution。 否则,你的程序应该输出一个符合要求的道路维护方案,也就是保持免费的 道路列表。按照输入中给定的那样输出免费的道路。如果有多种合法方案,你可 以任意输出一种。
样例输入
5 7 2
1 3 0
4 5 1
3 2 0
5 3 1
4 3 0
1 2 1
4 2 1
样例输出
3 2 0
4 3 0
5 3 1
1 2 1
Solve
-
这道题简化一下题意就是求一个生成树
-
我开始想的是先随意铺 k 条鹅卵石路,再铺 n-1-k 条水泥路,可是这样是不对的,有可能会有一些鹅卵石路必须铺才能使得图联通,而我的写法就可能不选这样的路。
-
所以跑两遍Kruskal,第一遍先铺水泥路,再铺鹅卵石路找出必须铺的鹅卵石路,第二遍先铺必须铺的鹅卵石路,再铺余下的鹅卵石路,最后铺水泥路。
Code
#include <cstdio>
using namespace std;
const int N = 2e4 + 5, M = 1e5 + 5;
struct Node {
int x, y;
}a[M][2];
struct Node2 {
int x, y, c;
}ans[N];
int tot[2], n, m, k, cnt, f[N];
int Find(int x) {
return x == f[x] ? x : (f[x] = Find(f[x]));
}
bool Add(int k, int m) {//k表示路的种类,m表示限制加的边数
int s = 0;
for (int i = 1; i <= tot[k]; ++i) {
int x = a[i][k].x, y = a[i][k].y;
int fx = Find(x), fy = Find(y);
if (fx == fy) continue;
f[fx] = fy;
ans[++cnt] = (Node2) {x, y, k};
if (++s == m) return 1;
}
return 0;
}
void print() {
for (int i = 1; i < n; ++i)
printf("%d %d %d\n", ans[i].x, ans[i].y, ans[i].c);
puts("");
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; ++i)
f[i] = i;
while (m--) {
int x, y, c;
scanf("%d%d%d", &x, &y, &c);
a[++tot[c]][c] = (Node) {x, y};
}
Add(1, tot[1]);
cnt = 0;
Add(0, tot[0]);
if (cnt > k) return puts("-1"), 0;//如果必须铺的路数不够k条,无解
for (int i = 1; i <= n; ++i)
f[i] = i;
for (int i = 1; i <= cnt; ++i)
f[Find(ans[i].x)] = Find(ans[i].y);
if (Add(0, k - cnt) && Add(1, n - 1 - k)) print();
else puts("-1");//如果两中路任意一种铺不够数量,无解
return 0;
}
C. T3(双递增序列)
题目描述
- 考虑一个长度为偶数 n 的序列 \(a_1, a_2, \dots, a_n\),我们称这个序列为好的,当且仅当存在 a1,a2,…,an\(a_1, a_2, \dots, a_n\)a1,a2,…,an 的一个划分 \(U=\{ a_{i_1}, a_{i_2}, \dots, a_{i_{n/2}} \}, V=\{ a_{j_1}, a_{j_2}, \dots, a_{j_{n/2}} \}=\{ a_1, a_2, \dots, a_n \}-U\),且 \(i_1<i_2< \dots <i_{n/2}, a_{i_1}<a_{i_2}< \dots <a_{i_{n/2}}, j_1<j_2< \dots <j_{n/2}, a_{j_1}<a_{j_2}< \dots <a_{j_{n/2}}\)。
- 比如序列 \(3, 1, 4, 5, 8, 7\) 就是一个好的序列。因为它可以分成 \(U=\{3, 4, 8\}, V=\{1, 5, 7\}\)。而序列 \(3, 2, 1, 6, 5, 4\) 则不是一个好的序列。
- 现在的问题是,针对给出的若干序列,请你判断它们是否是好的序列。
输入格式
- 第一行仅包含一个整数 m,表示需要判断 m 个序列。
- 接下来的 m 行分别给出这些序列。每个序列的输入为一行,每行的第一个数为一个偶数 n,表示序列的长度,随后的 n 个整数表示序列本身的元素 \(a_1, a_2, \dots, a_n\)。同一行的各数之间用一个空格隔开。
输出格式
- 输出 m 行,如果第 i 个序列为好的序列,那么第 i 行输出Yes!,否则输出 No!。
样例输入
2
6 3 1 4 5 8 7
6 3 2 1 6 5 4
样例输出
Yes!
No!
说明/提示
- 对于 10% 的数据,\(n \le 100\)。
- 对于 40% 的数据,\(n \le 300\)。
- 对于 100% 的数据,\(1 \le n \leq 2000, 1 \le m \leq 25, 0 \le a_i \le 10^6\)
Solve
- 分成两个序列 U,V,在进行的时候,第二个序列的末尾越小越好。
- 定义\(f_{i,j}\)表示前 i 个数,第一个序列长为 j,以 i 结尾,第二个序列长为 i-j ,最后一位的最小值。转移都是从 i-1 转移过来的,分为两种情况:
- 将 \(a_i\)放在 \(f_{i-1,k}\) 的第一个序列后面,需满足条件 \(a_i > a_{i-1}\) ,可知此时 i 长为 j 所以由 i-1 长度为 k=j-1 的状态转移而来:f[i][j] = min(f[i][j], f[i-1][j-1])
- 将 \(a_i\)放在\(f_{i-1,k}\) 的第二个序列后面,需满足条件 \(a_i > f_{i-1,k}\),可知此时第二个序列长为 i-j ,并未改变,所以是由 i-1 长度为 k=i-j 的状态转移而来:f[i][j] = min(f[i][j], a[i-1]),这里注意两个序列的变化。
- 题目上如果是求单调不下降序列就是代码里注释的内容。
Code
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2005, M = 0x3f3f3f3f;
int T, n, a[N], f[N][N];
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
memset(f, 0x3f, sizeof(f));
f[0][0] = -1;//f[0][0] = 0;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= min(i, n >> 1); ++j) {
if (a[i] > a[i-1]) f[i][j] = min(f[i][j], f[i-1][j-1]);
//if (a[i] >= a[i-1]) f[i][j] = min(f[i][j], f[i-1][j-1]);
if (a[i] > f[i-1][i-j]) f[i][j] = min(f[i][j], a[i-1]);
//if (a[i] >= f[i-1][i-j]) f[i][j] = min(f[i][j], a[i-1]);
}
puts(f[n][n>>1] == M ? "No!" : "Yes!");
}
return 0;
}
D. T4(Count on a tree)
题目描述
- 不知道为什么,但是你现在有一棵树。
- 这棵树包含 n 个结点,且每个节点有一个权值。
- 你需要支持以下操作:
- 询问点 u,v 之间路径上第 k 大权值是多少,保证 u 到 v 路径至少含有 k 个点。
输入格式
- 第一行有两个整数 n,m ,表示树上结点个数以及询问次数。
- 接下来一行有 n 个整数 \(val_i\),表示每个点的权值,整数之间用空格隔开。
- 接下来 n-1 行每行有两个整数 u,v,表示结点 u 和结点 v 之间有一条边。
- 接下来 m 行每行有三个整数 u,v,k,表示询问结点 u 和结点 v 之间路径上权值第 k 大的点的权值。
输出格式
- 对于每次询问,你应该输出一个整数表示答案,每个询问占一行。
样例输入
5 4
1 2 3 4 5
1 2
2 3
2 4
1 5
1 3 3
2 5 2
4 5 1
1 4 2
样例输出
1
2
5
2
数据范围与提示
- 对于 20% 的数据,保证\(n,m\le 500\)
- 对于另外 30% 的数据,保证树是一条链,但不保证 i 与 i+1 相连。
- 对于 100% 的数据,保证 \(n,m\le 10^5\)
Solve
- 数上可持久化线段树(主席树)
- 查询范围是root[x] + root[y] - root[lca(x, y)] - root[fa[lca(x,y)]]
Code
#include <cstdio>
#include <algorithm>
#define lson t[rt].l, l, mid
#define rson t[rt].r, mid + 1, r
using namespace std;
const int N = 1e5 + 5;
struct Side {
int t, next;
}e[N<<1];
int head[N], tot;
void Add(int x, int y) {
e[++tot] = (Side) {y, head[x]};
head[x] = tot;
}
struct Tree {
int l, r, s;
}t[N*20];
int n, m, a[N], b[N], f[N][21], d[N], trc, root[N];
void Change(int &rt, int l, int r, int x) {
t[++trc] = t[rt]; rt = trc;
++t[rt].s;
if (l == r) return;
int mid = l+r >> 1;
x <= mid ? Change(lson, x) : Change(rson, x);
}
int Ask(int x, int y, int lca, int flca, int l, int r, int k) {
if (l == r) return l;
int mid = l+r >> 1, s;
s = t[t[x].l].s + t[t[y].l].s - t[t[lca].l].s - t[t[flca].l].s;
if (s >= k) return Ask(t[x].l, t[y].l, t[lca].l, t[flca].l, l, mid, k);
else return Ask(t[x].r, t[y].r, t[lca].r, t[flca].r, mid + 1, r, k - s);
}
void Dfs(int x) {
int num = lower_bound(b + 1, b + b[0] + 1, a[x]) - b;
Change(root[x] = root[f[x][0]], 1, b[0], num);
d[x] = d[f[x][0]] + 1;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].t;
if (y == f[x][0]) continue;
f[y][0] = x;
Dfs(y);
}
}
int Jump(int x, int k) {
int i = 0;
while (k) {
if (k & 1) x = f[x][i];
k >>= 1; ++i;
}
return x;
}
int Lca(int x, int y) {
if (d[x] < d[y]) swap(x, y);
x = Jump(x, d[x] - d[y]);
if (x == y) return x;
for (int i = 20; i >= 0; --i)
if (f[x][i] != f[y][i])
x = f[x][i], y = f[y][i];
return f[x][0];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]), b[i] = a[i];
sort(b + 1, b + n + 1);
b[0] = unique(b + 1, b + n + 1) - b - 1;
for (int i = 1; i < n; ++i) {
int x, y;
scanf("%d%d", &x, &y);
Add(x, y); Add(y, x);
}
root[0] = ++trc;
Dfs(1);
for (int i = 1; i <= 20; ++i)
for (int x = 1; x <= n; ++x)
f[x][i] = f[f[x][i-1]][i-1];
while (m--) {
int x, y, k;
scanf("%d%d%d", &x, &y, &k);
int lca = Lca(x, y);
k = d[x] + d[y] - d[lca] * 2 + 1 - k + 1;
printf("%d\n", b[Ask(root[x], root[y], root[lca], root[f[lca][0]], 1, b[0], k)]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号