动态规划(一)
动态规划
接下来我将持续更新这篇关于动态规划的学习文章并发表博客,如有错误欢迎大家的纠正。
入门:递推与动态规划
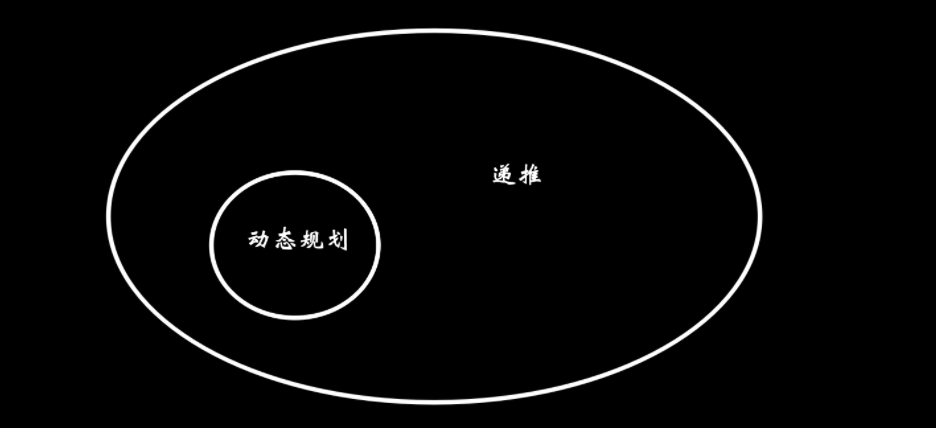
通过数学归纳法产生各种公式
数学归纳法的三个步骤:
确定边界条件是成立的。
如果公式的第n-1项是成立的,那么该公式的第n项也一定是成立的。
如果前面都是对的,那么当递推到最后一步时,最终的结果也一定是成立的。
而通过数学归纳法可以推出各种公式,例如下面的斐波那契数列。
公式有意义吗?
我认为公式本身是没有意义的,只有当公式对应到某个具体的问题场景并且为解决这个问题而服务时,这个公式才被这个问题赋予了某种特定的意义,我认为可以将公式理解为是问题的答案的抽象化结果。
例如:斐波那契数列的公式为\(F(n) = F(n-1)+F(n-2)\),这个公式乍一看是没有意义的,但是如果将他放置到下面的这个问题中时,他瞬间就有意义了。
问题:爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
思路:
已知有两种爬楼梯的方法:要么走一个台阶,要么走两个台阶。那么如果我设置一个函数\(F(n)\),这个函数的意义是走到第n级台阶时的方法总数。
那么他要走到第n级台阶,有两种方式:一种是从(n-1)级台阶走一步到终点;一种是从(n-2)级台阶跨两部到达终点。所以我们可以理解为走到第n级台阶的方法总数\(F(n)\)是走到第n-1级台阶的方法总数\(F(n-1)\)加上走到第(n-2)级台阶的方法总数\(F(n-2)\)之和。及\(F(n) = F(n-1)+F(n-2)\)。你看,这是这个式子就有意义了,他的意义就是解决上面这个问题。
代码演示:
using namespace std;
class Solution
{
public:
int climbStairs(int n)
{
vector<int> stair(1000);
stair[0] = 1;
stair[1] = 1;
for (int i = 2; i <= n; i++)
{
stair[i] = stair[i - 1] + stair[i - 2];
}
return stair[n];
}
};
结果:
同时,数学归纳法的思想也运用到了上面的代码中。

用递归的实现方式是
class Solution {
public:
int climbStairs(int n) {
if (n == 0 || n == 1) {
return 1;
}
return climbStairs(n - 1) + climbStairs(n - 2);
}
};
代码执行结果是
那么究竟如何解决递推问题呢?
-
确定递推状态(重点)
确定你这个递推函数的功能 确定你这个函数的自变量有哪些,这些自变量的意义是什么? 确定你这个函数的因变量是什么? -
确定递推公式(\(K_i \to K_{i+1}\))
n
3. 确定边界条件
4. 程序实现:递归或者循环。
==递推状态最重要!!!==
==递推状态最重要!!!==
==递推状态最重要!!!==
==递推状态 = 函数符号+对于这个函数符号的定义==
例如:
就像上面的爬楼梯问题
1. 你先确定函数符号的作用就是计算出==爬到某一级台阶时的方法总数==
2. 其次,这个函数的因变量是你目前所爬到阶梯数,而函数的因变量就是你要求的方法总数。自变量就是一般就是位于函数括号里面的量,而函数的因变量就是等号另一边的项。
但是,再刷题之前,我认为有必要先学学`滚动数组`的知识。



