哈夫曼编码
哈夫曼编码树
首先要知道什么是编码:
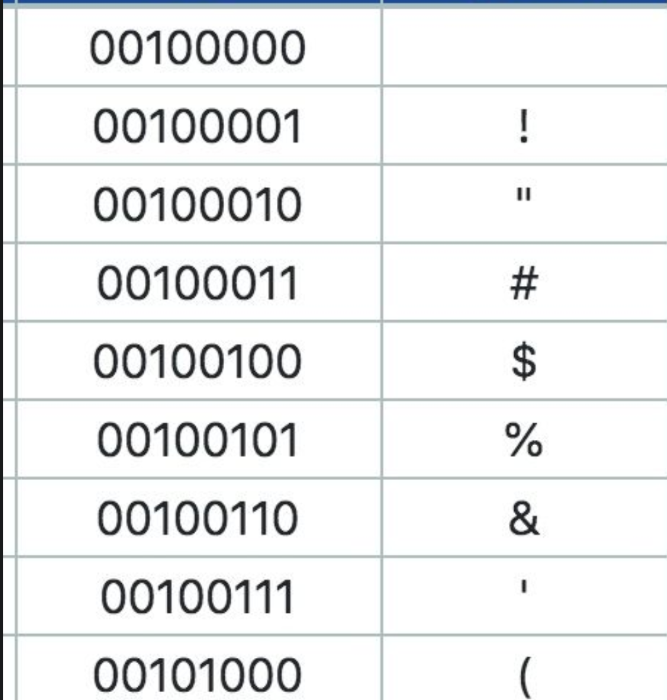
就像上图一样,左边是编码,右边是字符,所以左边到右边的变换就是解码,右边到左边的变换就是编码。但这是有8位,所以只能表示128位字符,这对英语是够用的了,但是对其他语言例如汉语,日语确实远远不够用,那该怎么办呢?此时就有了多字节编码。
但是多字节编码也是有漏洞的,就像是假设我要用多字节编码,但是如果我只输入字符A,那么编码就是00000000 00000000 00000000 01000001,这其实是十分浪费空间的,所以就出现了Unicode。
Unicode(编码字符对应表)
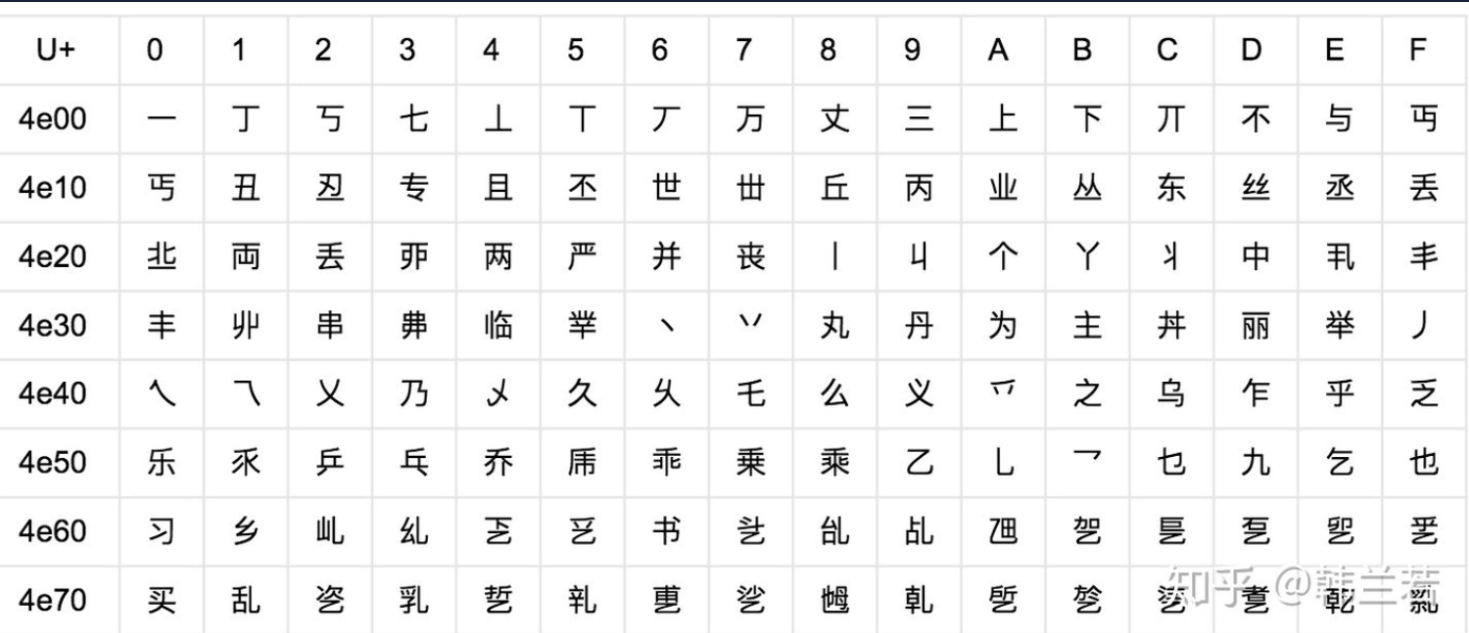
Unicode本身不是一种编码,而是一个表,对于每个字符都是U+一个16进制数字来表示。这时国际公认的规则,所有由它诞生的编码都是根据它的规则所指定的。例如假设这个字符“x”在这个表中已经规定是这个16进制数,那么进行编码成其他二进制数时这个二进制数的大小一定是等于表中所对应的二进制数的大小的。
同时这个统一编码下面分有8为字节编码,16位字节的编码,32位字节的编码。

UTF-8(可变编码)
UTF-8是一种变长编码,就是这个编码的长度可以8位8位的依次增长,同时,UTF-8可以根据Unicode编码所对应的16进制数自动转化为对应的二进制数。例如:
- 我要输出字符B,因为字符B的位数本身就是小于8位的,所以他是可以直接用UTF-8进行编码和解码输出。
- 我要输出字符“牛”,容易知道字符“牛”是不能直接用UTF-8的八位二进制输出的,所以我可以先将“牛”这个字符在Unicode表中查找到的16进制数找出来,假设这个16进制数所对应的范围是000080-0007FF,那么当他转化为字节流时,UTF-8就会自动变成16位二进制数输出。
编码的种类:
- 变长编码:就是像UTF-8这种编码长度可以改变的编码方式。
- 定长编码:就是像UTF-16这样编码长度已经固定了的编码方式。
编码的使用场景
信息的传输,因为在信道中,信息是以二进制的方式进行传输的,所以要将信息进行二进制编码,对于不同形式的二进制组合方式,都代表一个不同的信息。
平均编码长度
- 平均编码长度的计算方式:平均编码长度 = 每个字符的编码长度*每个字符的出现概率。
- 意义:平均编码长度越短,说明发送一段相同数据流,所发送的二进制流就越短,发送的效率就越高。
哈夫曼树
哈夫曼树的生成方式就是利用了平均编码长度这个概念。生成步骤如下:
- 首先计算出每个字符的生成概率。
- 这颗树每个叶结点都代表一个字符,同时从根节点和叶结点都代表一个二进制数0或者1.
- 每要读取一个字符,都是按照左0右1的方式读取出来。
假设有数据流中各个字符的出现概率:
a: 0.8,b: 0.05,0: 0.1,1: 0.05
那么最终形成的树的形状为:
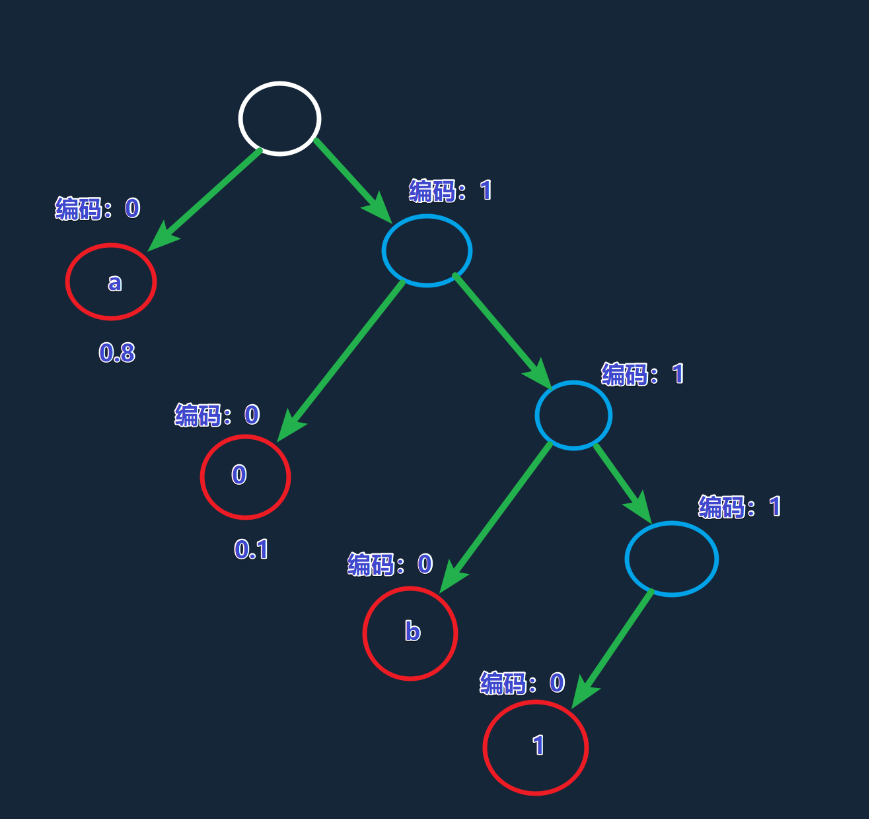
那么通过这颗哈夫曼树所得到的哈夫曼编码就是
- a : 0
- 0 : 10
- b : 110
- 1 : 1110
可见出现的概率越大的字符所对应的二进制就越长。
代码演示:
class Node {
public:
Node* lchild, * rchild;
char ch;
double p;
Node(char c, double p, Node* l, Node* r) :ch(c), p(p), lchild(l), rchild(r) {}
};
Node* root;
class tree {
private:
vector<Node*> arr;
public:
void insert(char c,double p) {
arr.push_back(new Node(c, p, NULL, NULL));
}
void pick_min(int n) {
for (int i = n - 1; i >= 0; i--) {
if (arr[n]->p > arr[i]->p) {
swap(arr[n], arr[i]);
}
}
return;
}
Node* make_tree() {
int len = arr.size();
for (int i = 1; i < len; i++) {
pick_min(len - i);
pick_min(len - i - 1);
arr[len - i - 1] = combine(arr[len - i], arr[len - i - 1]);
}
return arr[0];
}
Node* combine(Node* a, Node* b) {
Node* n = new Node('\0', a->p + b->p, a, b);
n->lchild = a;
n->rchild = b;
return n;
}
void output(Node* root,string str,int k = 0) {
if (k >= str.size()) {
str.push_back('0');
}
if (root->lchild == NULL && root->rchild == NULL) {
printf("%c: %s\n", root->ch, str.c_str());
return;
}
str[k] = '0';
output(root->lchild,str, k + 1);
str[k] = '1';
output(root->rchild,str, k + 1);
return;
}
};
int main() {
tree* t = new tree();
int sum = 0;
string str;
double temp[26];
srand((unsigned int)(time(NULL)));
for (int i = 0; i < 26; i++) {
temp[i] = rand() % 1000;
sum += temp[i];
}
for (int i = 0; i < 26; i++) {
printf("%c 的出现概率为 %lf\n", 'A' + i, temp[i] / sum);
t->insert('A' + i, temp[i] / sum);
}
cout << "结果为" << endl;
root = t->make_tree();
t->output(root, str);
return 0;
}




