Machine Learning — 逻辑回归

现实生活中有很多分类问题，比如正常邮件/垃圾邮件，良性肿瘤/恶性肿瘤，识别手写字等等，这些可以用逻辑回归算法来解决。

一、二分类问题

所谓二分类问题，即结果只有两类，Yes or No，这样结果｛0，1｝集合来表示y的取值范围。

前面说到过，线性回归的模型是 h(x)=θ₀+θ₁x₁+θ₂x₂+...，这种回归模型的取值是在整个自然数空间的，对于0，1问题，就要想办法把模型取值压缩到0~1之间，这里我们就引入一个激活函数，可以用sigmoid函数：g(z)=1/(1+e^-z)，也可以用tan函数：t(x)=(e^z-e^-z)/(e^z+e^-z)，sigmoid函数的取值是[0,1]，tan函数的取值是[-1,1]。这里我们主要讨论sigmoid函数。

      

所以h_θ(x)=g(θ^Tx),它代表的意思是对于给定的x值，y取1的概率，即P(y=1|x)，我们的任务就是利用已有样本数据集去寻找一组参数θ，得到概论分布函数P(y=1|x)。

分界面

对于分类问题，应该有一个分界面来区分，但是我们通过h_θ(x)=g(θ^Tx)得到的值是[0，1]之间的数值，那么我们就认为当g(θ^Tx)>=0.5时，y=1，即概率0.5对应的是分界点，此时θ^Tx=0。

代价函数

代价存在的意义就是求解θ，衡量模型h_θ(x)与真值之间的差距，令其最小化，求得θ。

对于线性回归模型，我们用差的平方形式来表示代价函数，但是这种形式对于逻辑回归模型是不适用的，我们这里引入对数函数              

log这是一个很奇妙的函数，h_θ(x)取值是[0,1]，

如果y=1，代价函数为-log(h_θ(x))，取值是[0，+∞)。这时若h_θ(x)→0，-log(h_θ(x))→+∞，即代价函数→+∞；反之，则代价函数→0。

同样的，y=0的情况下也是如此。所以对数函数形式的代价函数很好的表现了模型预测值与真值之间的差异。更进一步简化模型，可以以下函数来同时涵盖这个分段函数

Cost(h_θ(x),y)=-log(h_θ(x)^y)-log((1-h_θ(x))^(1-y))

于是，对于m个样本的数据集，我们可以用以下函数来表示其代价函数平均值（即经验风险）

要得到最佳模型，就是要计算一组θ值，使得J(θ)最小，这里同样可以用梯度下降法，而且很神奇的是，这里的梯度函数和线性回归模型的形式是一样的。我特地证明了一下，感兴趣的同学点这里：Machine Learning — 逻辑回归的Gradient Descent公式推导

在Ng视频中，还介绍了计算计算代价函数最小值的高级算法，这里就不展开了。

 

二、多分类问题

实际上，除了Yes No分类问题之外，还有很多多分类问题，很典型的就是识别阿拉伯数字，从0-9一共有10个数字。求解的方法是类似的，只不过多一个维度。

对于二分类问题，θ是一个向量，一组数，问题只包含一个模型，最后得到的结果是一个概率值。

对于多分类问题（假设有k类），θ是一个(n+1)*k的矩阵，相当与是k个二分类问题的组合，包含k个模型，最后得到的结果是一个k维的向量，k个概率值，哪个最大就说明属于哪类。

 

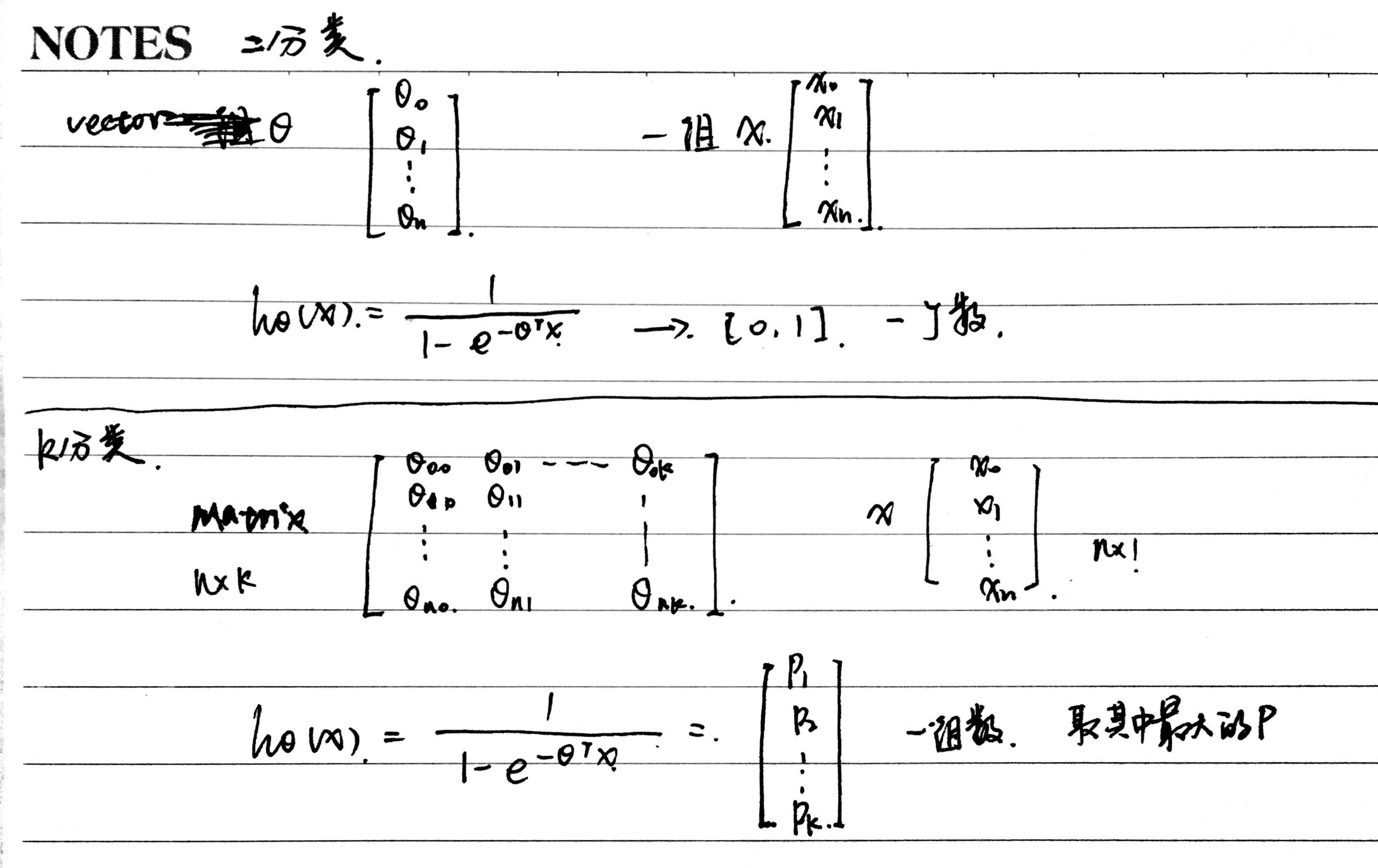
那如何去得到这个矩阵θ呢？用循环一列一列计算。

以Ng课程中的识别手写的0-9数字为例，这里有10个分类。用像素值最为input参数，假设有m个样本，每个样本对应的y值是1-10中的某一个（这里用y=10代替y=0）。

建立这样一个循环，

for i=1 to 10

   令样本中所有y=i的y为1，其余为0，这就变成了二分类问题，样本中的y非0即1

   找到对应的θ向量

end

将所有向量组合成矩阵，h_θ(x)得到的结果就是10*1的向量，比如说其中第三个值最大，说明模型认为手写字是3的概率最大。