3. 变换编码理论基础 Theoretical Foundations of Transform Coding
3. 变换编码理论基础 Theoretical Foundations of Transform Coding
本文主要讲述一种编码方式，对应上一篇博客中，将图片编码为latent representation的算法
论文地址为Theoretical Foundations of Transform Coding
本文主要讨论了几种有损信源编码的方案，信源编码组成为编码器+解码器，将像素级的向量映射为长度更短的比特信息，再通过解码器映射回来。
如FFT的本质，在做编码和信号处理时，经常会涉及到分治策略，分而治之的思想也广泛应用在检索、排序、卷积等多种计算需求中。图像的信源编码的效率依赖于像素点之间的相似性和强关联性，比如目标的像素连续性、边界性等特征；然而实际上图像较大时，一般采用有损压缩实现高效的压缩，按照以下三步实现：
- 线性变换，实现将像素域数据转换为变换域的离散数据，减少数据量。
- 量化过程，设置不同量化区间实现量化和压缩
- 熵编码，对量化结果进行分布统计和对应的熵编码
信源编码的编码过程可以表示为两个映射，即α和γ的级联：α表示从原数据域到变换域的集合映射，而γ表示变换域的集合和比特串(码字)的可逆映射，有损信源编码中，α是有损的编码器，而γ对应的是无损的码字（熵编码），其中α为不可逆映射，可以看作线性映射+量化两步实现，因为在编码中，量化必然引入不可逆的误差，包含在α中，映射为量化后的码字，而γ是对这些离散的码字再次进行编码，降低比特长度。解码同理，流程如下图：
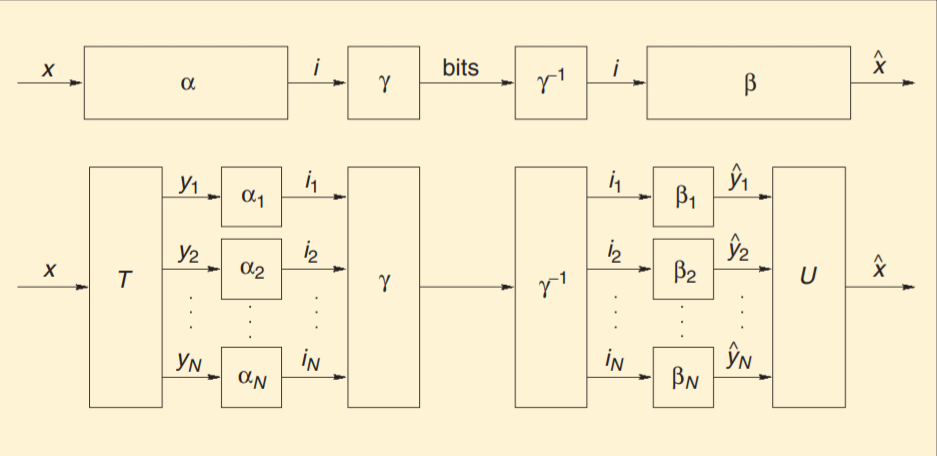
压缩的效果和性能分别从压缩效率和误差两方面看，分别以输出的比特数和均方差(the mean-squared error,MSE)表征。 每次进行变换的像素点个数N在选择上很有讲究，既可以是一张图片所有像素点个数，也可以是其中的一小块区域；如果选择得较大，那么预测性能会好，但是计算复杂度也会相应提升(密码本内容更多，索引更久)。而目前最先进的方法也是取了一种折中，不是最优，但相对较好，这样面对像素点较多N较大的图像时，依然可以适用。
线性变换
依照前面所讲的三步，其中，线性变换对应的可以是
FFT
余弦变换
小波变换
DCT变换
KL变换(KLT)等
其主要目的是降低数据域的连续性和数据量，将数据从像素值变换到频域，方便后续的量化+编码，有效地提高编码效率。而KL变换作为图像压缩中一种最优正交变换，拿来作为例子。（变换+可视化）
...
分级量化
量化部分即引入了噪声，本质是对域空间进行分割量化，将连续的值域变成离散的集合，有效降低了数据熵值，也同时导致了有损编码。由于线性变换后常常是复数值，因此可以按照极坐标形式表示这些数据，进行量化分割。
量化分割时，也分为两种：有约束(Constrained)和无约束(Unconstrained),其区别在于分割是否规则。如果按照极坐标统计，那么可以以原点为中心的射线和以原点为圆心的圆线作为分割的标准之一。
量化的阶梯越小，量化的损失也就越小，同时量化后的阶梯数目也越多，熵值也更大，所以这也是一个平衡问题，如果按照均匀量化和均匀白噪声来看，R = log2(N) , D=(Δ^2)/12.
熵编码
熵编码最典型的比如哈夫曼编码，已知信源概率分布情况后，通过概率分配合适的码字，使得平均总码长最短。
常见熵编码方法：哈夫曼、算术编码等。
