【概率论】条件概率 & 全概率公式 & 朴素贝叶斯公式

---

 

0. 说明

　　条件概率 & 全概率公式 & 朴素贝叶斯公式 学习笔记

 

　　参考

　　scikit-learn机器学习（五）--条件概率，全概率和贝叶斯定理及python实现

 

---

1. 条件概率

　　【定义】

　　已知 事件A 发生的条件下，另一个 事件B 发生的概率成为条件概率，即为 P(B|A)

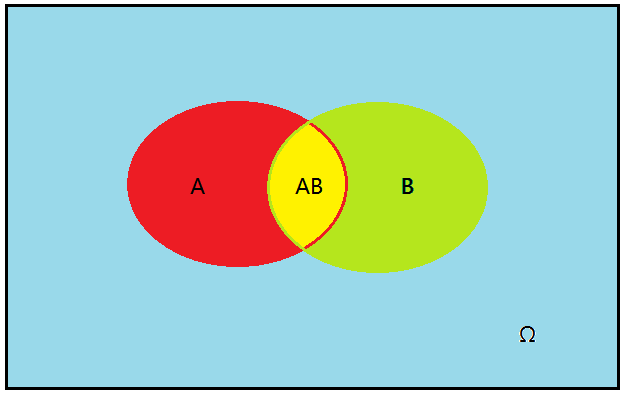
　　如图 A∩B 那一部分的发生的概率即为 P(AB)

 

P(AB) = 发生A的概率 * 发生A之后发生B的概率 = 发生B的概率 * 发生B之后发生A的概率

　　即：

P(AB) = P(A) * P(B|A) = P(B) * P(A|B)

　　所以条件概率公式：

P(B|A) = P(AB) / P(A) = P(B) * P(A|B) / P(A)

　　

 

 

　　P(A) 是 A 的先验概率
　　P(A|B) 也叫做 A 的后验概率

 

 

---

2. 全概率公式

 

 

 

---

3. 朴素贝叶斯公式

 

 

 

 

---