用回溯算法解决四皇后问题

前言
回溯法 1-求n个元素的集合的幂集中状态变化树是一棵满二叉树：树中每个叶子结点的状态都是求解过程中可能出现的状态（即问题的解）。
【然而】很多问题用回溯和试探求解时，描述求解过程的状态树不是一棵满的多叉树

【非满多叉树】不是满的多叉树：当试探过程中出现的状态和问题所求解产生矛盾时，不再继续试探下去，这时出现的叶子结点不是问题的解的终结状态
此类问题的求解过程可看成是在约束条件下进行先序（根）遍历，并在遍历过程中剪去那些不满足条件的分支

问题
求4皇后问题的所有合法布局（作为例子，把八皇后问题简化为4皇后问题）

思路
四皇后问题的棋盘状态树：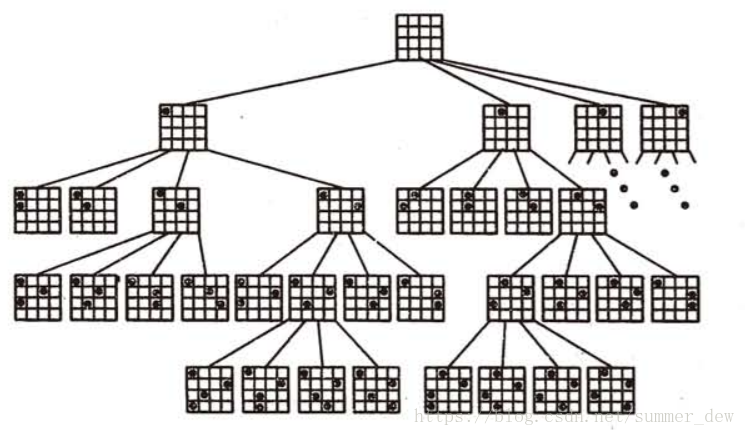

这是一棵四叉树，树上每个结点表示一个局部布局或一个完整的布局

【根结点】棋盘的初始状态，棋盘上无任何棋子
【规则】每个棋子都有4个可选择的位置
但在任何时刻，棋盘的合法布局都必须满足3个约束条件，即任何两个棋子都不占据棋盘的同一行、或者同一列、或者同一对角线

求所有合法布局的过程即为在上述约束条件先根遍历图中的状态树的过程

做法
遍历中访问结点的操作为：判别棋盘上是否已得到一个完整的布局（即棋盘上是否已摆上4个棋子）

是：输出该布局
否：依次先根遍历满足约束条件的各棵子树，即首先判断该子树根的布局是否合法
合法：先根遍历该子树
否则：剪去该子树分支

void Trial(int i, int n) {
	// 进入本函数时，在n×n棋盘前i-1行已放置了互不攻击的i-1个棋子
	// 现从第i行起继续为后续棋子选择合适位置
	// 当i>n时，求得一个合法的布局，输出之
	if (i>n) 输出棋盘的当前布局； //n为4时，即4皇后问题
	else {
		for (j=1; j<=n; j++) {
			在第i行第j列放置一个棋子；
			if (当前布局合法)
				Trial(i+1, n);
			移走第i行第j列的棋子；
		}
	}
}

　　

该算法可作为回溯法求解的一般模式，类似问题有骑士游历、迷宫问题、选最优解问题等