关于对使用补码数最透彻的理解

先从下面一小段代码入手，说明其中的道理

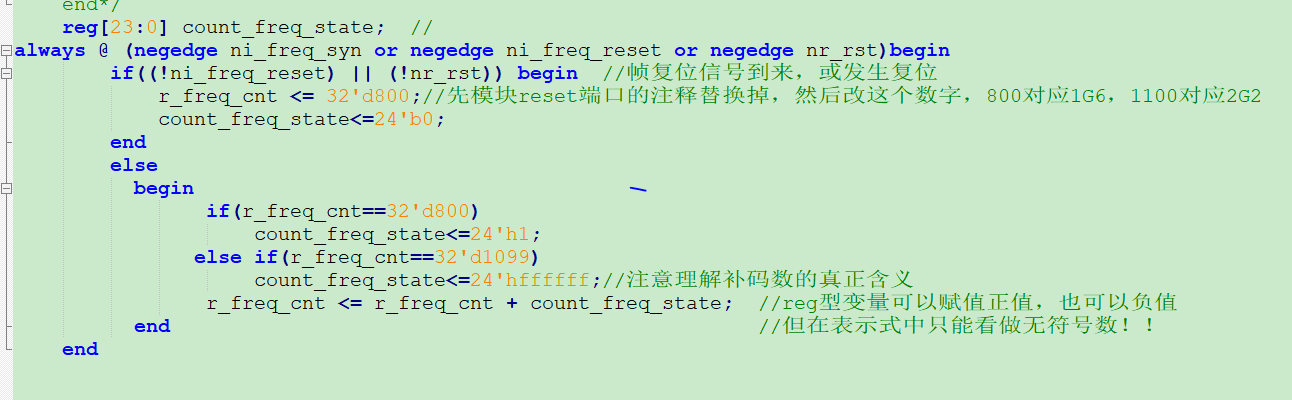
上面这段代码的作用是，使得变量 r_freq_cnt能够循环往复从800逐渐+1变化到1100，再逐渐-1变化到800，循环往复，类似于随着时间的推移生成了一个三角波。核心在于，如何在r_freq_cnt=1099的时候，导致使得r_freq_cnt=r_freq_cnt+1，变成r_freq_cnt=r_freq_cnt-1？而理解这个问题的核心在于，如何理解数？或者说如何理解寄存器中的计数？

寄存器计数的过程是，从0计到最大值（并没有有符号和无符号这种概念）会发生溢出，最大值再加1，计数器归0，再从新计数。这便是计数的本质。我们所关注数的大小，无非就是关注寄存器这个容器中装了多少个数而已。当我们加上1个数（假设没有溢出），这个数变大了。但如果我们加了一个比较大数，导致寄存器溢出了，那么计数器的本质可能会使得寄存器中的数反而比原来小。举个简单的例子：

假设有一个3位的寄存器，则计数最大计到7（111），再加1变成了000；

       假设现在寄存器中的数为（101），也就是5.再加1时，变成了110，也就是6.此时得到的数比原来的大，也就是没有溢出.

       假设，我们现在，再加上4，那么根据计数的本质，寄存器中的值实际为001，也就是1.发现此时数反而变小了。这其实反映了数的本质———计数！！

       那么既然能通过加法实现将数变小，那么这其中本来就有一种减法的思想在里面。那么加多少刚好减1呢。我们发现，刚好加上计数器容器的大小，也就是模值，刚好实现减1.

       对于这里，5要想减1变成4，必须要加7.那么如何解读这个结果呢。而我们发现，补码数的根本思想其实本质上就是这种循环计数的思想。

      因此上述程序中，给出了减1其实就是加上了24位寄存器的最大值。这同时也给了我们这样一个信息，参加运算的两个数必须是等位宽的才有意义。

     从本质上讲，当我们在理解负数的补码表示的时候，我们不应该把负数当成一种数，应该把它当成0减去这个数，比如-3，应该当成0-3这个过程！！！！那么怎么实现这个减法呢，当然是通过加一个很大的数让其溢出，这也就导致了补码的诞生！！！