IP核引发的关于定,浮点数的认识

上面是一段关于CORDIC_IP测试文件,用于计算给定角度的sin值和cos值,关于数值表示规则在此不再重复,仅仅说明以下3点:
1 数采用原码,反码,补码,本身并没有正确与否之分(这一点很重要,我们不能认为只有补码的表示是正确的),有的只是适用场合,采用补码的方式能够使得使得加法和减法变得统一,而采用原码自然也有它的好处。
2 在编写Verilog文件时,不管是源文件,还是测试文件,出现小数是一种错误的做法(准确的说直接将小数作为输入输出信号或者中间变量,或者作为测试信号)都是不正确的。永远需要记住的是,数的表示永远是 :位宽+'进制+相应进制下的数。这才是开发环境 以及FPGA本身所允许的数据格式。(否则会出现不太满意的数据)。
3 2说明了我们对于想要处理的小数,通常要通过某种规则转化成符合数表示方式的数,有定点表示和浮点表示两种方法,在FPGA中,更多的是定点数,因此更多的采用定点的转换方法。需要额外注意的是,这一步转换,需要我们自己完成,而不能够通过开发环境完成!
下面通过乘法器IP核进一步直观阐述上述3 :
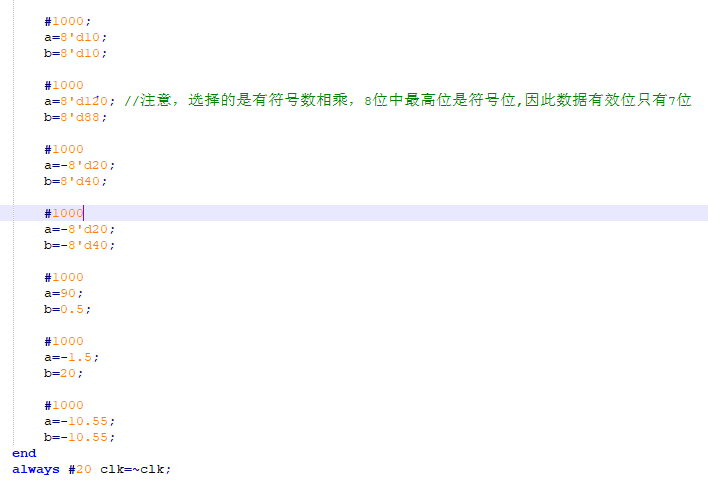
上述图是乘法器IP核的验证代码,其中a和b作为输入,p作为输出.从图中看出来,本人想通过赋值小数给测试信号输入端,来验证小数相乘(其实已经违背了数据的表示格式),观察输出波形如下:

观察上图,发现,对于符号数(带符号整数)的计算是正确的,但是发现输入的小数被近似成了整数,实际上这并不是我们希望得到的,我们想要得到的是小数的结果(需要注意的是,尽管这里显示的是十进制,但也只能显示整数,不能显示小数),而且计算结果也不对。
这提示我们:当面临小数输入(不管是仿真,还是实际中需要把数据输入到模块中去),必须要通过某种手段将这些小数转化成整数,进行乘法计算,再通过某种手段将结果变成我们要的小数(虽然我们不能直观的在波形上看出来)。但是在实际的数据处理中要求我们要这儿做,而这种方式就是:小数定点化(再次强调FPGA中定点数使用的更多)
同时也额外的得到这样的信息:FPGA中乘法器的IP核是定点的,而不是浮点的。
关于对数本身的理解:
在计算机中,并没有类似于,整数,小数,正数,负数这些概念.实际上也并不存在诸如,反码,补码,这些概念。唯一有一个概念就是计数器。计数器反应了数的本质。
对于有符号数,应该有这样一个认识:比如4位计数器,当我们记到0111也就是7的时候,再加1变成了1000,也就是-8,即最大的正数加1变成了最小的负数,同样的,最小的负数减一变成了最大的正数,这个概念我们一定要十分的明确,在我们进行计数的时候,这一点要尤其明确!!!!!1关键在于计数本身就是一个轮回的概念!!!!!这也反应了计算机对于数理解的本质!!!



