信号处理第一篇——浅谈正弦信号

在这篇博客中，我们不讨论有关于正弦信号数学层面的意义，而是将理论结合工程，讨论信号处理中一些要注意的事项。

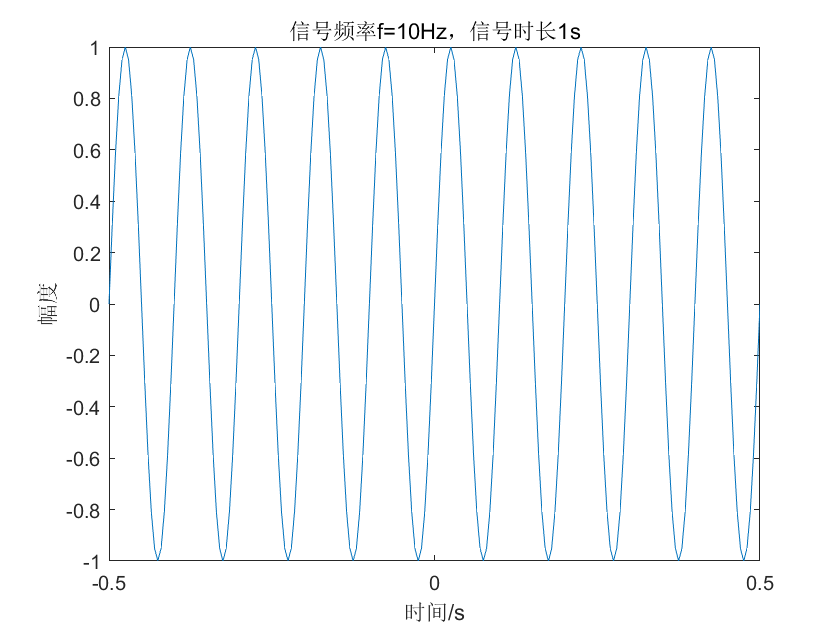
图 1

上图是一个用matlab生成的频率为10Hz的正弦信号，需要注意的是，matlab生成的正弦信号，本质是一组离散有限长度的周期信号。实际上，我们任何的一个数字信号系统（比如雷达系统），所得到的信号都是离散的，持续时间有限的信号。

我们对上述信号新型FFT处理，得到：

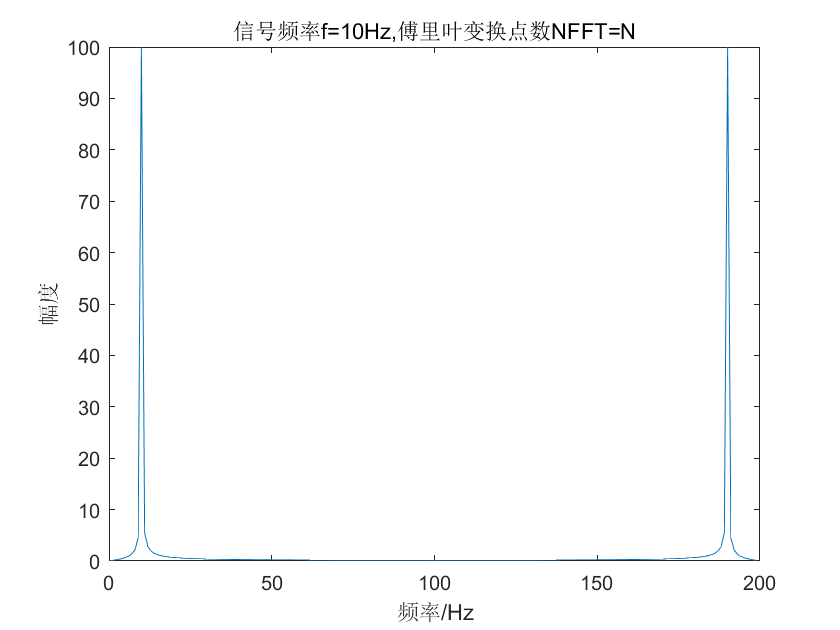
       图 2

在上述频谱图中，出现了两个峰值，可以看到第一个峰在10Hz左右的位置，这与信号的频率一致。还有一个峰出现在190Hz左右的位置。这是什么呢？按道理而言，正弦信号的确有两个峰。但是是关于零频(0Hz)对称的。也就是说另一个峰应该出现在频率等于-10Hz的地方。原因在于，FFT之后，得到是数组，显然，数组的索引代表了频率值，然而索引值显然是从1开始的，因此无法表示负频率。因此只能把-10Hz的频率成分放在最后，变成201-10Hz=190Hz。这也就是为什么我们在190Hz的地方看到峰的原因。使用fftshift函数，则可以得到我们想要的结果：

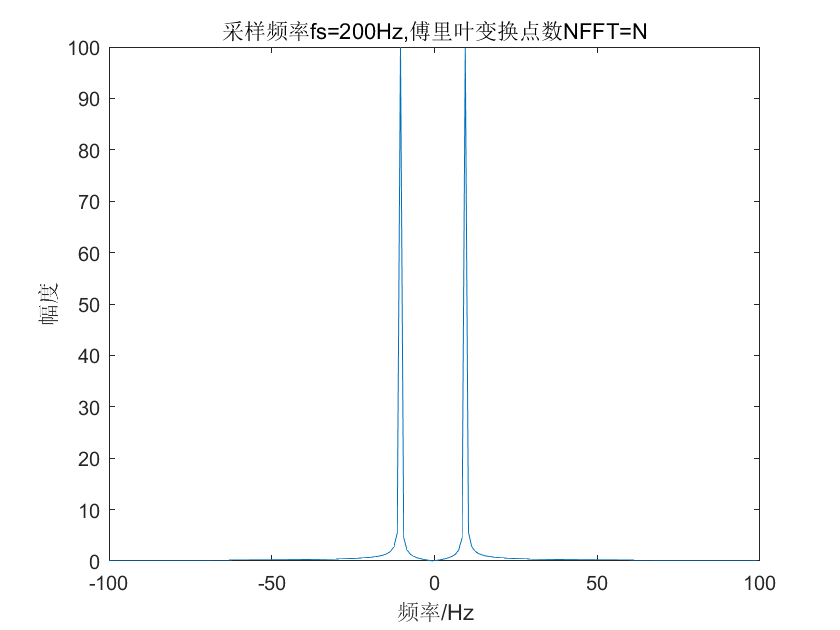
图 3

上图中，两个峰值分别出现在10Hz和-10Hz的位置，出现在正确的位置。

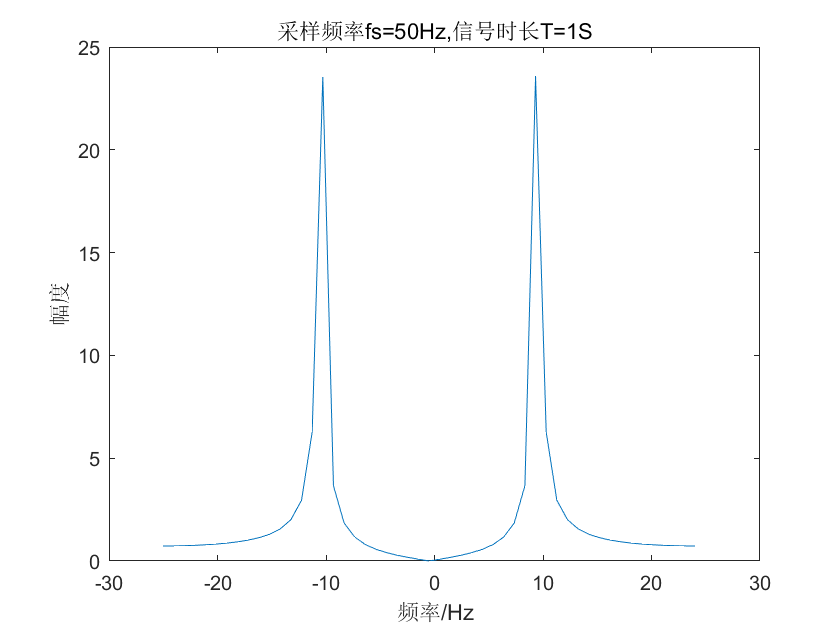
图 4

 对比图3和图4，可以看出，模拟信号的采样率提升了，则在采样周期相同的情况下，采样点数更多了，那么其对应的频率分辨率就更高。

图5

增加FFT点数，并不能提高频谱分辨率，但是可以细化频谱，图5中，可以较为清楚的看到频域信号的sinc函数的形状。

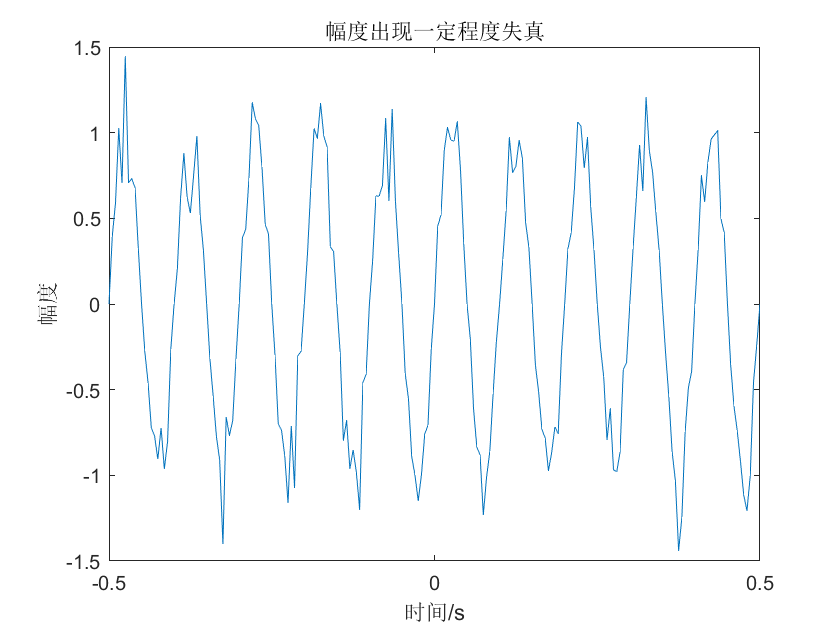
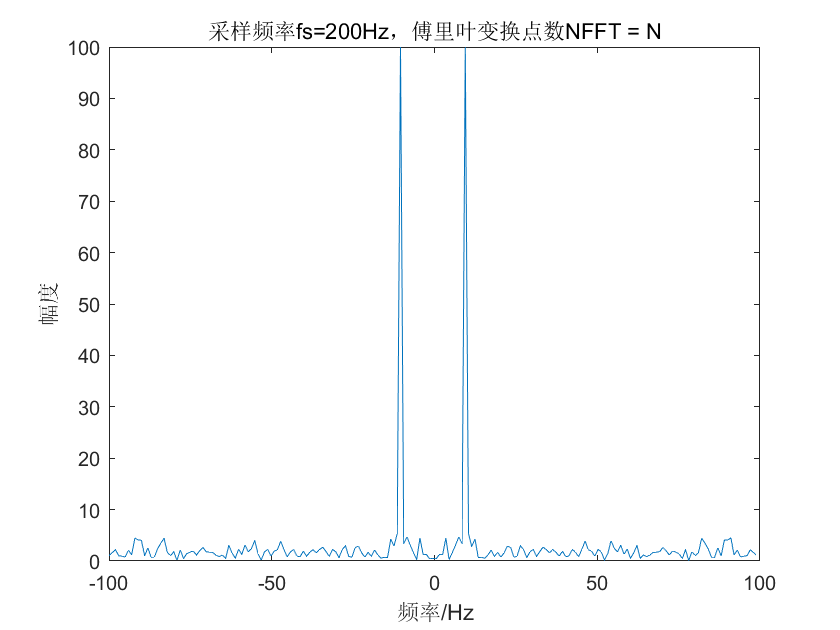
幅度失真后果

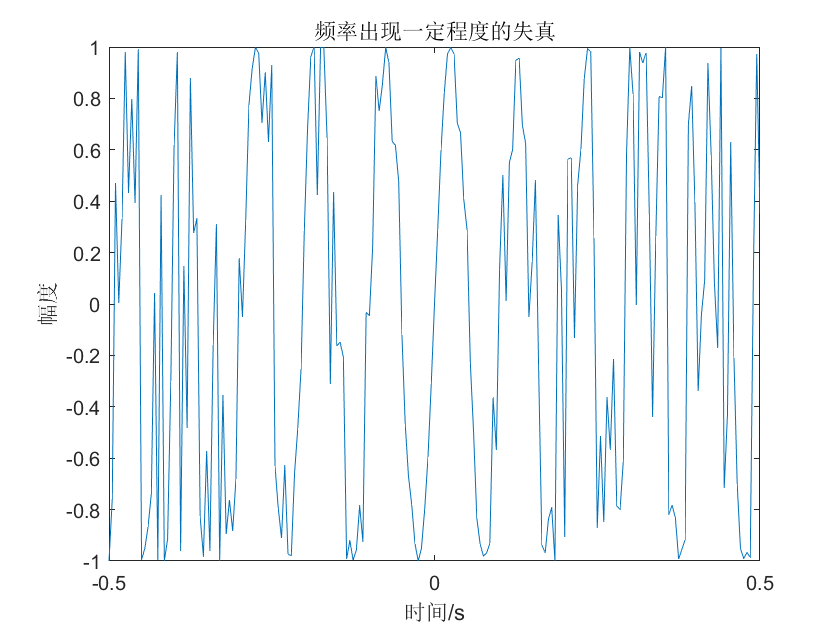
频率失真的结果

频率偏移的运行结果：

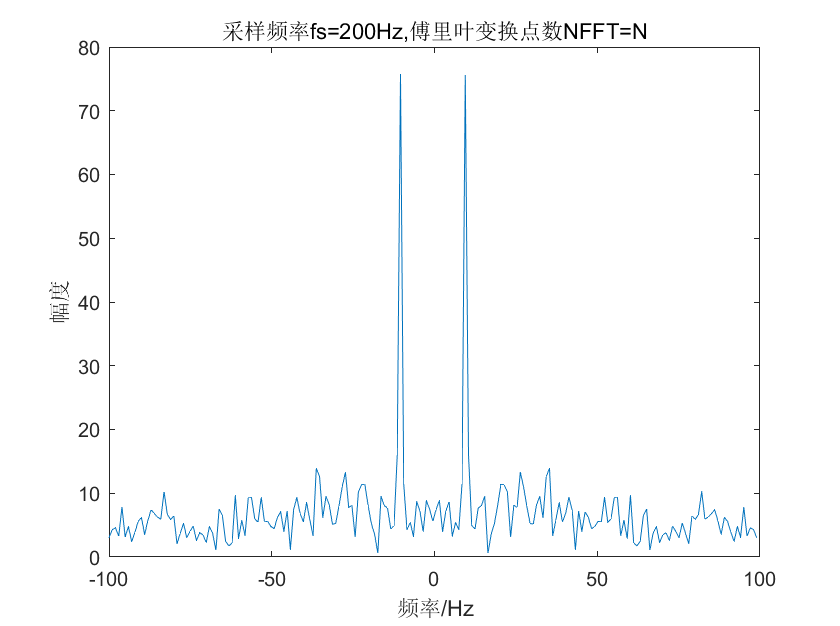
可见频率失真对于频谱的影响是非常大的。

 代码：

%%  正弦信号频谱分析，matlab代码
clear 
close all
clc
%% signal
A=1;                %幅度
f=10;               %频率
w=2*pi*f;           %
p=0;                %相位
%采样
T=1;                %s        %观测时间
fs=20*f;            %Hz       %采样频率
d=1/fs;             %s        %采样间隔
t0=-T/2:d:T/2;       %离散时间t
s1=A*sin(w*t0+p);    %正弦信号
figure(1)
plot(t0,s1);
xlabel('时间/s');
ylabel('幅度');
%% FFT
%FFT (这里会多一个镜像信号，但是位置不对)
NFFT = length(t0);
FFTres  = fft(s1,NFFT);
FFTAmu = abs(FFTres);
n = 0:NFFT-1;
ft0=n*fs/NFFT; %频率序列
figure(2)
plot(ft0,FFTAmu)
xlabel('频率/Hz');
ylabel('幅度');
title('信号频率f=10Hz,傅里叶变换点数NFFT=N');
%% 采用fftshift将对称干扰信号搬移到正确位置。
FFTres  = fftshift(fft(s1,NFFT));
FFTAmu = abs(FFTres);
ft=(-NFFT/2:NFFT/2-1)*fs/NFFT; %频率序列
figure(3)
plot(ft,FFTAmu)
title('采样频率fs=200Hz,傅里叶变换点数NFFT=N')
xlabel('频率/Hz');
ylabel('幅度');
%%  改变采样频率，看结果会怎么样
fs=5*f;            %Hz       %采样频率，10倍信号频率
T=1;                %s        %观测时间，信号长度
%采样间隔
d=1/fs;             %s        %采样间隔
t1=-T/2:d:T/2;       %离散时间t
s1=A*sin(w*t1+p);    %正弦信号
NFFT1 = length(t1);
FFTres  = fftshift(fft(s1,NFFT1));
FFTAmu = abs(FFTres);
ft1=(-NFFT1/2:NFFT1/2-1)*fs/NFFT1; %频率序列
figure(4)
plot(ft1,FFTAmu)
% 结果表明采样频率降低之后，信号频谱分辨率会降低
%从另外一个角度讲，
title('采样频率fs=50Hz,信号时长T=1S')
xlabel('频率/Hz');
ylabel('幅度');
%% 改变傅里叶变换的点数
fs=20*f;            %Hz       %采样频率，10倍信号频率
T=1;                %s        %观测时间，信号长度
%采样间隔
d=1/fs;             %s        %采样间隔
t1=-T/2:d:T/2;       %离散时间t
s1=A*sin(w*t1+p);    %正弦信号
NFFT = 8*length(t1);
FFTres  = fftshift(fft(s1,NFFT));
FFTAmu = abs(FFTres);
ft=(-NFFT/2:NFFT/2-1)*fs/NFFT; %频率序列
figure(5)
plot(ft,FFTAmu)
% 结果表明采样频率降低之后，信号频谱分辨率会降低
%从另外一个角度讲，
title('采样频率fs=200Hz,傅里叶变换点数NFFT = 4*N')
xlabel('频率/Hz');
ylabel('幅度');
%% 改变信号持续周期
fs=5*f;            %Hz       %采样频率，10倍信号频率
T=4;                %s        %观测时间，信号长度
%采样间隔
d=1/fs;             %s        %采样间隔
t2=-T/2:d:T/2;       %离散时间t
s1=A*sin(w*t2+p);    %正弦信号
NFFT = length(t2);
FFTres  = fftshift(fft(s1,NFFT));
FFTAmu = abs(FFTres);
ft=(-NFFT/2:NFFT/2-1)*fs/NFFT; %频率序列
figure(6)
plot(ft,FFTAmu)
title('采样频率fs=50Hz,信号时长T=4S')
xlabel('频率/Hz');
ylabel('幅度');
%% 假设信号的初始相位不为0，会发生什么？
A=1;                %幅度
f=10;               %频率
w=2*pi*f;           %
p=pi/3;             %相位
%采样
T=1;                %s        %观测时间
fs=20*f;            %Hz       %采样频率
d=1/fs;             %s        %采样间隔
t0=-T/2:d:T/2;       %离散时间t
s1=A*sin(w*t0+p);    %正弦信号
NFFT = length(t0);
FFTres  = fftshift(fft(s1,NFFT));
FFTAmu = abs(FFTres);
ft=(-NFFT/2:NFFT/2-1)*fs/NFFT; %频率序列
figure(7)
plot(ft,FFTAmu)
title('采样频率fs=20f,信号观测时长T =1s,初始相位p=pi/3')

%% 假设信号的幅度有失真，会发生什么？
f=10;               %频率
w=2*pi*f;           %
p=0;                %相位
%采样
T=1;                %s        %观测时间
fs=20*f;            %Hz       %采样频率
d=1/fs;             %s        %采样间隔
t0=-T/2:d:T/2;       %离散时间t
NFFT = length(t0);
% 随机生成幅度值
pd = makedist('Normal',1,0.2)     % Normal(mu,sigma)
pdt = truncate(pd,0.5,1.5)              % truncated to interval (0,1)
numRows = 1;
numCols  = NFFT;
A = random(pdt,numRows,numCols);  % Sample from distribution `pdt`
s1=A.*sin(w*t0+p);    %正弦信号
figure(8)
plot(t0,s1);
xlabel('时间/s');
ylabel('幅度');

FFTres  = fftshift(fft(s1,NFFT));
FFTAmu = abs(FFTres);
ft=(-NFFT/2:NFFT/2-1)*fs/NFFT; %频率序列
figure(9)
plot(ft,FFTAmu)
title('采样频率fs=20f,信号观测时长T =1s')
%% 
%% 假设信号的频率有失真，会发生什么？
A=1;                %幅度
p=0;                %相位
%采样
T=1;                %s        %观测时间
fs=20*10;            %Hz       %采样频率
d=1/fs;             %s        %采样间隔
t0=-T/2:d:T/2;       %离散时间t
NFFT = length(t0);
% 随机生成幅度值
pd = makedist('Normal',10,0.5);     % Normal(mu,sigma)
pdt = truncate(pd,9,11) ;             % truncated to interval (0,1)
numRows = 1;
numCols  = NFFT;
f= random(pdt,numRows,numCols);  % Sample from distribution `pdt`
w=2*pi.*f;           %
s1=A.*sin(w.*t0+p);    %正弦信号
figure(10)
plot(t0,s1);
xlabel('时间/s');
ylabel('幅度');

FFTres  = fftshift(fft(s1,NFFT));
FFTAmu = abs(FFTres);
ft=(-NFFT/2:NFFT/2-1)*fs/NFFT; %频率序列
figure(11)
plot(ft,FFTAmu)
title('采样频率fs=20f,信号观测时长T =1s')

%% 处理接收两路的回波信号
A=1;                %幅度
f1=10;               %频率
f2=25;
w1=2*pi*f1;     
w2=2*pi*f2;        
p=0;
%采样
T=1/10;                %s        %观测时间
fs=20*f2;            %Hz       %采样频率
d=1/fs;             %s        %采样间隔
t0=-T/2:d:T/2;       %离散时间t
s1=A*sin(w1*t0+p)+A*sin(w2*t0+p);    %正弦信号
figure(10)
plot(t0,s1);
FFTres  = fftshift(fft(s1,NFFT));
FFTAmu = abs(FFTres);
ft=(-NFFT/2:NFFT/2-1)*fs/NFFT; %频率序列
figure(12)
plot(ft,FFTAmu)
title('采样频率fs=20f,信号观测时长T =1s')