牛客网剑指offer第23题——二叉搜索树的后续遍历序列
题目：
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
思路分析：
由于是二叉搜索树,即BST树。则其中序遍历就是按照大小顺序排列的。后续遍历就是：先遍历左子树，再遍历右子树，再遍历根节点。而要遍历的树是BST树，则左子树所有节点value<根节点<右子树。即如下图所示：
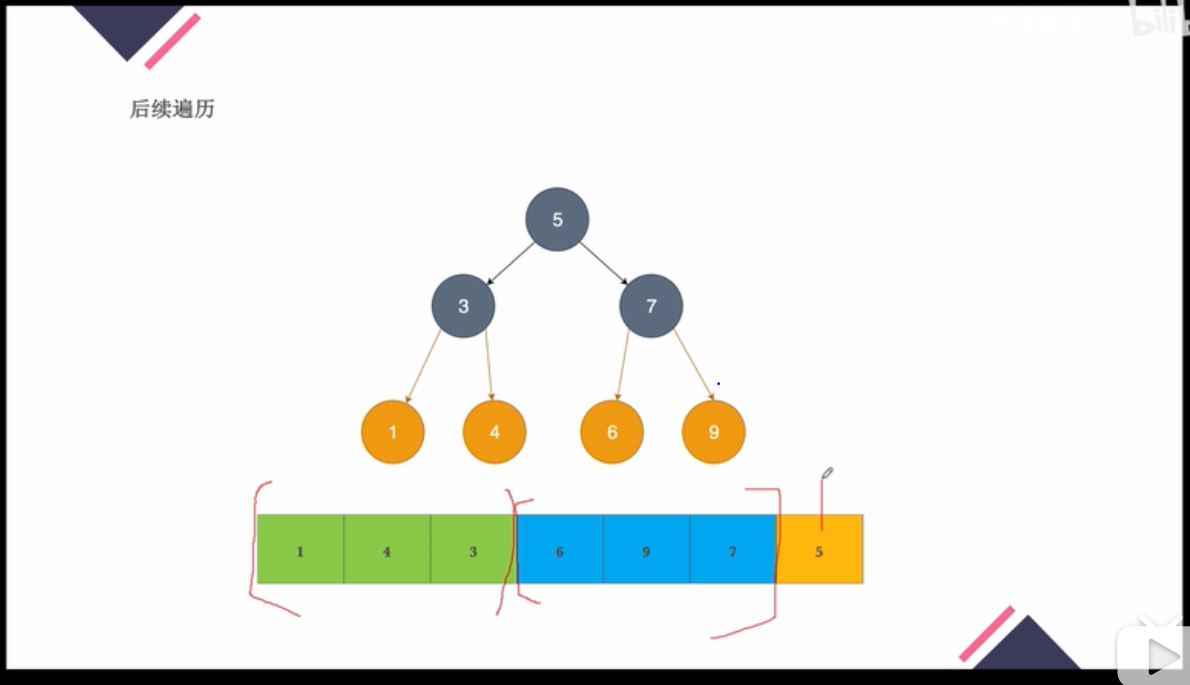
我们可以看到，左子树是小于根节点的，右子树是大于根节点的。
那么，我们该如何判断是不是后续遍历呢？也就是数组到底符合什么规律才是后续遍历？看下图：
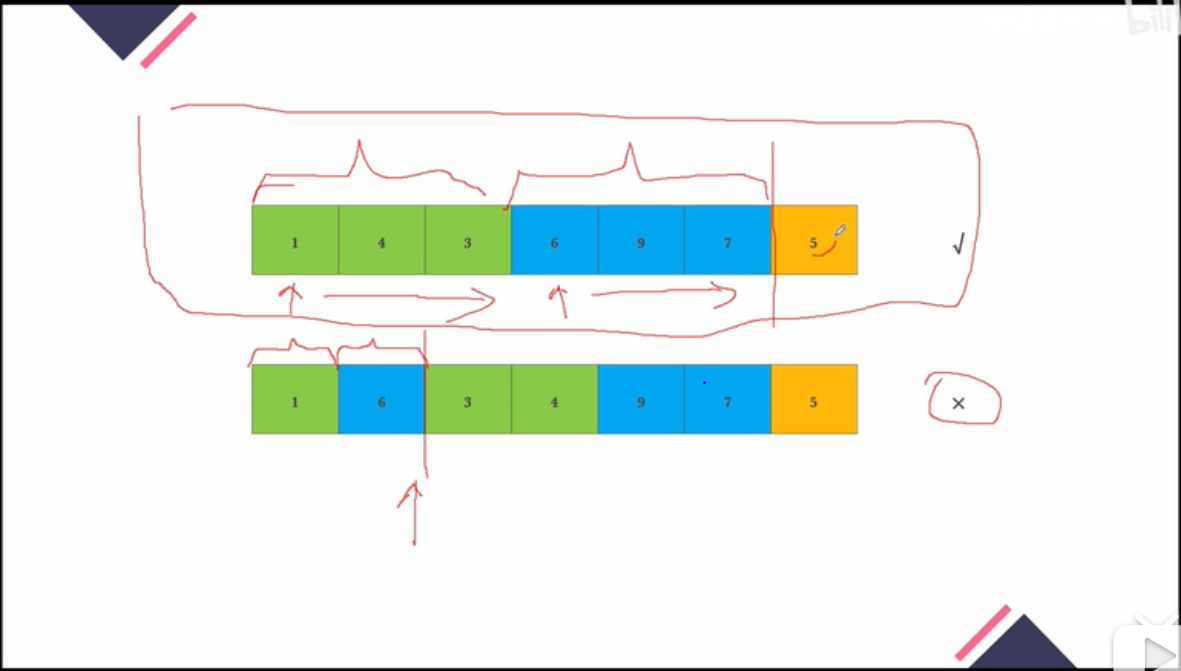
上图表明，我们索引所有小于node的数作为当前node的左子树value，大于node的数作为右子树value。在正常情况下：这个索引index应该等于array.size-1；也即是node 前面的数恰好被分成了两部分；比如上图下面那个例子。没有访问到结尾，就要结束了，显然，这并不是后续遍历。
当对当前node进行了判断之后，对其左右子树做同样的判断。
先给出代码：再给出关于递归的一些总结：
1 class Solution { 2 public: 3 bool VerifySquenceOfBST(vector<int> sequence) { 4 //注意题设有说明是二叉搜索树 5 int length = sequence.size(); 6 if(length < 1) 7 return false; 8 if(length == 1) 9 return true; 10 vector<int>left,right; 11 int index = 0; 12 int node = sequence[length-1];//头节点 13 while(sequence[index] < node) 14 { 15 left.push_back(sequence[index]); 16 index++; 17 } 18 while(sequence[index] > node) 19 { 20 right.push_back(sequence[index]); 21 index++; 22 } 23 if(index < (length-1)) 24 return false; 25 if(left.size() == 0) 26 return VerifySquenceOfBST(right);//y要考虑有一侧为空的情况 27 else if(right.size() == 0) 28 return VerifySquenceOfBST(left); 29 else 30 return VerifySquenceOfBST(left)&&VerifySquenceOfBST(right); 31 } 32 };
分析：我并没有像其他人一样采用两个函数递归调用，而是只用了一个函数，我的思想是什么呢？
先处理数组为空，此时返回false；因为我知道要将输入数组划分为左右子树，并递归进行判断。当然了25-30行的代码需要注意的是：假如递归到一定程度，左子树为空，或者右子树为空，我们应该判断另一棵树；当然了如果两者都不为空，则都要判断。最终，我们给出了递归的终止条件：也就是第8行的代码，即数组中只有一个元素，即只有一树节点，此时返回true。
根据上个题目。我们对递归解决bool返回值的问题做一个总结：
第一步：边界判断（当然了，这是所有的时候都要做的，上述代码6-7行）
第二步：给出递归子结构时输入参数的表达式（比如上述中的left和right，上述代码10-22行）
第三步：给出当前步骤中，返回失败的条件（上述代码23-24行）
第四步：给出子结构递归的表达式（上述代码25-30行）
第五步：给出递归终止条件（该问题有解的条件，上述代码8-9行）
上述步骤中，第二步和第四步是非常重要的，甚至是可能比较困难的。
从上述步骤中，抽象出我理解的一般递归的步骤：
第一步：给出递归子结构时输入参数的表达式
第二步：给出子结构递归的表达式
第三步：给出递归终止条件
我认为处理递归问题时候，应该严格按照上述三个步骤来，并且顺序不能搞反了！
