图像处理中的求导问题

图像处理中导数和模板的求法

图像处理中使用的导数

copyright 版权所有，严禁抄袭，转载需获得本人授权,邮箱：zhaogoodwell@gmail

前言

　　工欲善其事必先利其器，在图像处理中最常用的数学基础有导数、卷积。今天我们主要讨论下数字图像处理中的导数，从从连续函数的导数概念出发，再到离散情况下的导数，最后使用代码来实现。所有只讲理论，不给处实例代码的行为都是耍流氓！！！

连续函数导数的一般性定义

　　设有定义域和取值都在实数域中的函数 y=f(x)y=f(x). 若 f(x)f(x) f(x); 在点 x0x0的某个邻域内有定义，则当自变量 xx 在x0x0 处取得增量 ΔxΔx（点 x0+Δxx0+Δx 仍在该邻域内）时，相应地 yy 取得增量Δy=f(x0+Δx)−f(x0)Δy=f(x0+Δx)−f(x0)；如果 ΔyΔy与 ΔxΔx 之比当 Δx→0Δx→0 时的极限存在，则称函数 y=f(x)y=f(x) 在点 x0x0; 处可导，并称这个极限为函数y=f(x)y=f(x) 在点 x0x0 处的导数，记为 f′(x0)f′(x0)，即：

 

f′(x0)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δxf′(x0)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δx

 

这是导数的定义，需要用到极限，显然这儿公式没法在离散情况下套用，在离散情况下我们怎么来计算导数呢？差分。

离散情况下的差分计算

　　在离散情况下我们利用差分来代替微分，差分分为两种，前向差分和后向差分。我们假设有一个数列x(n)x(n),n,h∈N+n,h∈N+,我们有：

前向差分求导　

df=x(n)−x(n−h)hdf=x(n)−x(n−h)h

后向差分求导

df=x(n+h)−x(n)hdf=x(n+h)−x(n)h

差分求导和导数形式上是一样的，区别在于没有使用极限，所以利用差分来求导是一种不精确的方法，我们把hh称作步长，显然步长越小越好，就越接近导数的真实值，精度会越高。差分求导在数值分析里面有广泛的使用。我们就拿一个微分方程仿真为例，来说明如何使用离散导数解决问题。我们知道f(x)=exp(−(x−μ)22σ2)f(x)=exp⁡(−(x−μ)22σ2)的导数是f′(x)=−x−μσ2f(x)f′(x)=−x−μσ2f(x) 我们可以使用差分来仿真这个微分方程。对这个方程改写如下：

f(x+Δx)−f(x)Δx=−x−μσ2f(x)f(x+Δx)−f(x)Δx=−x−μσ2f(x)

　化简可得：

f(x+Δx)=(1−x−μσ2Δx)f(x)f(x+Δx)=(1−x−μσ2Δx)f(x)

　 我们可以设置一个很小的步长每次对进行迭代，可以得出函数的数值解。

我们使用如下Python 代码对它进行仿真。

# -*- coding: utf-8 -*-
"""
@author: zhao
"""


import numpy as np
import matplotlib.pyplot as plt

def g(x):
    return np.exp(-((x-mu)**2)/(2*sigma**2))

sigma = 1.6
mu = 2
x = np.linspace(-6,10,200)


plt.plot(x,g(x))
plt.title('g(x)')
plt.show()



it = [200,2000,20000]
for step in it:
    x = np.linspace(-6,10,step)
    f = np.zeros(x.shape)
    delta = x[1] - x[0]
    f[0] = g(-6)
    for i in np.arange(1,step):
        f[i] = (1 - delta * (x[i-1]-mu)/(sigma**2)) * f[i-1]
    plt.plot(x,f)
    plt.title("step="+str(step))
    plt.show()
    

执行结果：

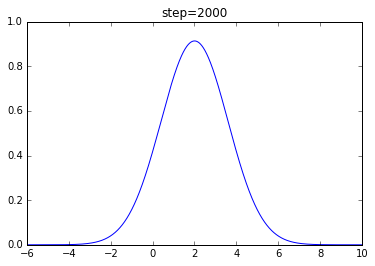
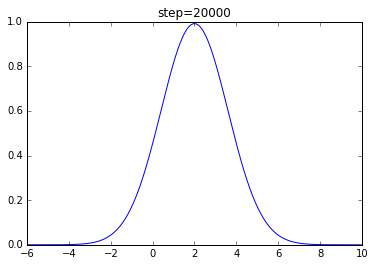
图像导数实现

我们对图像很多操作都是用模板来实现的，比如图像的梯度，滤波，边沿提取等技术。我们所说的图像处理一般是指数字图像，是对模拟信号的采样，对图像进行求导的操作只能通过差分等方式来实现。对待一幅图像我们定义它的xx方向上的导数为gx=f(x+1)−f(x)gx=f(x+1)−f(x)，但是这样没有一个中心点我们操作起来不方便，所以我们就把这个模板进行扩展，所以我们采用如下模板来计算图像的xx和yy方向的梯度:

 

gx=−1−1−1000111gx=−101−101−101

 

 

gy=−101−101−101gy=−1−1−1000111

 

下面我们用最后得出梯度的幅值为G(x,y)=(g2x+g2y)−−−−−−−−√G(x,y)=(gx2+gy2)方向为: θ=arctangygxθ=arctan⁡gygx现在我们用程序来实现这个过程。

拉普拉斯算子，在数学上的表达式为：

 

L(x,y)=∂f(x)∂x(2)+∂f(y)∂y(2)L(x,y)=∂f(x)∂x(2)+∂f(y)∂y(2)

 

这个是对图像xx和yy方向两次求导，然后相加。我门先看xx方向的一阶导数，gx=f(x,y)−f(x−1,y)gx=f(x,y)−f(x−1,y)，再对以一阶导数求导便是二阶导数,最终结果为：

 

gxx=gx(x+1)−gx(x)=f(x+1,y)−f(x,y)−(f(x,y)−f(x−1,y))=f(x+1,y)−2∗f(x,y)+f(x−1,y)gxx=gx(x+1)−gx(x)=f(x+1,y)−f(x,y)−(f(x,y)−f(x−1,y))=f(x+1,y)−2∗f(x,y)+f(x−1,y)

 

最后同理可得：

 

gyy=f(x,y+1)−2∗f(x,y)+f(x,y−1)gyy=f(x,y+1)−2∗f(x,y)+f(x,y−1)

 

最后可得：

 

L(x,y)=∂f(x)∂x(2)+∂f(y)∂y(2)=f(x+1,y)−4∗f(x,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)L(x,y)=∂f(x)∂x(2)+∂f(y)∂y(2)=f(x+1,y)−4∗f(x,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)

 

用3x的模板可以表示为：

 

0−10−14−10−1−00−10−14−10−1−0

 

最后代码实现为：

"""
@author: zhao
"""

import numpy as np 
import cv2
import matplotlib.pyplot as plt

img = cv2.imread('lena1.tiff')
img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
img = np.array(img,dtype= np.float64)
g_x = np.array([[-1,0,1],[-1,0,1],[-1,0,1]])
g_y = np.array([[-1,-1,-1],[0,0,0],[1,1,1]])
laplace = np.array([[0,-1,0],[-1,4,-1],[0,-1,0]])

img_g_x =cv2.filter2D(img,-1,g_x)
img_g_y =cv2.filter2D(img,-1,g_y)
img_laplace = cv2.filter2D(img,-1,laplace)

img_graid = np.sqrt(img_g_x **2 + img_g_y **2)
img_angle = np.arctan(img_g_y/(img_g_x + 2**-1000))

plt.subplot(2,3,1),plt.imshow(img,cmap ='gray'),plt.title('source'),plt.xticks([]),plt.yticks([])
plt.subplot(2,3,2),plt.imshow(img_g_x,cmap ='gray'),plt.title('x gradient'),plt.xticks([]),plt.yticks([])
plt.subplot(2,3,3),plt.imshow(img_g_y,cmap ='gray'),plt.title('y gradient'),plt.xticks([]),plt.yticks([])
plt.subplot(2,3,4),plt.imshow(img_graid,cmap ='gray'),plt.title('gradient  amplitude'),plt.xticks([]),plt.yticks([])
plt.subplot(2,3,5),plt.imshow(img_angle,cmap ='gray'),plt.title('angle'),plt.xticks([]),plt.yticks([])
plt.subplot(2,3,6),plt.imshow(img_laplace,cmap ='gray'),plt.title('Laplace'),plt.xticks([]),plt.yticks([])

在图像处理中里面有很多跟导数有关的模板，比如在SIFT代码中需要hessian矩阵，大体上按以上流程，基本都能实现计算出需要的模板。