牛客网剑指offer第21题——判断出栈序列是否是入栈序列
题目:
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
先上通过的代码:
1 class Solution { 2 public: 3 bool IsPopOrder(vector<int> pushV,vector<int> popV) { 4 bool isoder = false; 5 int i = 0; 6 int j = 0; 7 stack<int> pushs; 8 if(pushV.size()&& popV.size()) 9 { 10 while(i < pushV.size()) 11 { 12 while((pushs.empty())||(j<popV.size()) && (pushs.top() != popV[j]) ) 13 { 14 pushs.push(pushV[i]); 15 i++; 16 } 17 while((!pushs.empty())&& (j<popV.size())&& (pushs.top() == popV[j])) 18 { 19 pushs.pop(); 20 j++; 21 } 22 } 23 if(pushs.empty()) 24 isoder = true; 25 } 26 return isoder; 27 } 28 };
尽管这道题还有其他最为简单的办法,但是这里,我们不讲究任何技巧,介绍一种最为朴素的思想:
如果给出的序列是一种入栈数组的出栈序列,那么我们将这个数组数组入栈,并且按照某种规则出栈,那么最终会得到一个和给出序列一样的序列,并且这个栈最终会变成空栈!而我们判断这个序列是否是给出数组的一种出栈可能,就是看我们模拟出来的这个栈是否最终会变成一个空栈。
下面,我们探讨,上述提到的所谓出栈规则究竟是什么?
如果要验证所给的序列确实是入栈数组的出栈序列,我们应该做的就是:尽量对入栈序列按照给定的出栈方式出栈,如果最后全部元素出栈,即栈空,则表明所给出栈序列是正确的。下面我们具体的举例说明:
假设提供的是入栈序列是1、2、3、4、5;提供的出栈序列是 4 3 5 1 2;如何验证这个序列是否正确呢?
核心思路即上述所说:使得入栈序列的出栈方式尽量向所给出栈序列靠拢。下面我们来描述一下完整的思路:
假设提供的入栈顺序是:1、2、3、4、5 push(1) -> stack.top() = 1≠4,继续push push(2) -> stack.top() = 2≠4,继续push push(3) -> stack.top() = 3≠4,继续push push(4) -> stack.top() = 4=4,pop(4),出栈索引+1,此时指向了3 stack.top = 3 = 3,pop(3),出栈索引+1,此时指向了5。 stack.top = 2≠5,继续push push(5) ->stack.top = 5 = 5,pop(5),出栈索引+1,此时指向了2 stack.top = 2 = 2,pop(2),出栈索引+1,此时指向了1。 stack.top = 1 = 1,pop(1),出栈索引+1,此时指向了空。 **此时stack为空!!!,因此4、3、5、2、1是1、2、3、4、5的一个出栈序列**
上文已经给出类似于判决思路:模拟序列的入栈出栈过程,使其出栈向所给序列靠拢,若最后所有元素成功出栈,即栈空,表明所给序列是正确的。
下面针对上述代码,我们说明STL中栈stack的一一些函数。
push(x),将元素x入栈 pop(),将栈顶元素出栈,但是并不返回栈顶元素(返回类型为void) top(),返回栈顶元素,但是不删除栈顶元素(不执行pop功能),**若栈为空,执行top()返回-1** empty(),判断栈是否为空,**为空返回1,不空返回0**
其他函数以后遇到再说:
此题的延伸题目:给出一个入栈序列,求所有的出栈序列?(思考怎么做)
给出一个长度为n的序列,其所有的出栈可能数为:卡塔兰数
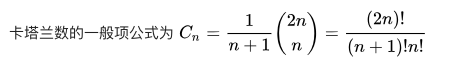
stay foolish,stay hungry



