开普勒一、二定律的(非常不严谨)证明
首先是一个几何题,我们最后会回收这个作为伏笔的题目:
给定一个圆(圆心为 )和一个圆内的点 ,任取圆周上一点 ,则 的中垂线必切以 为两焦点的椭圆。
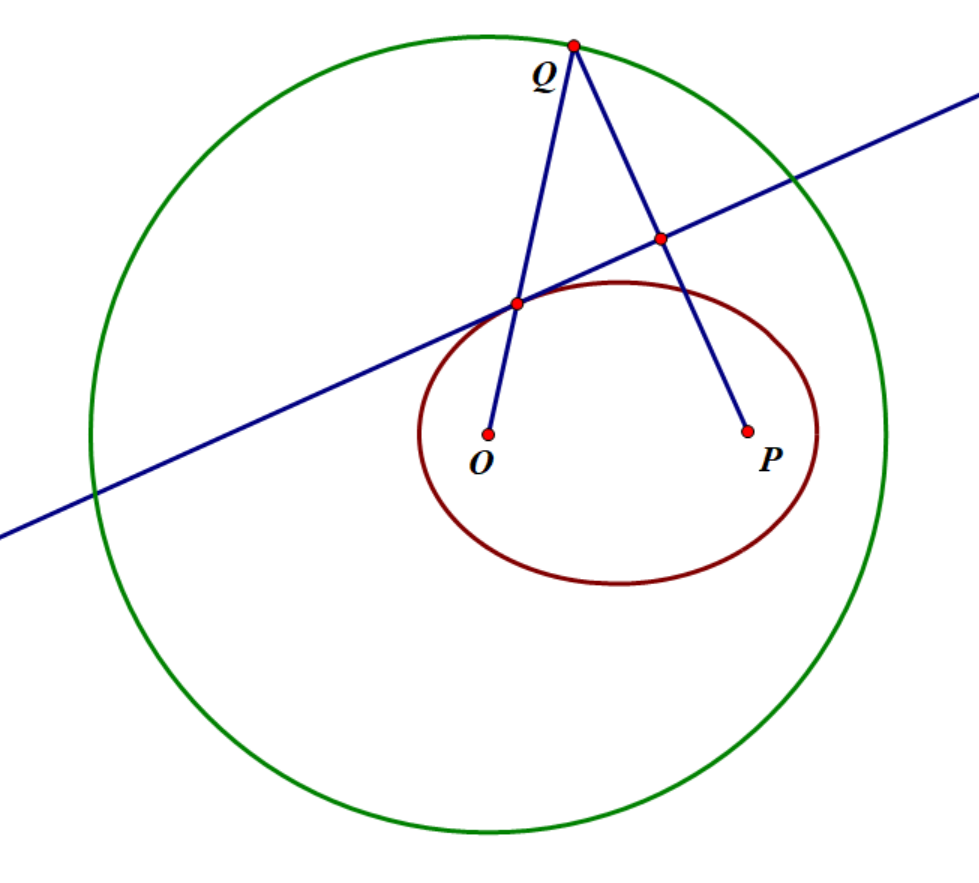
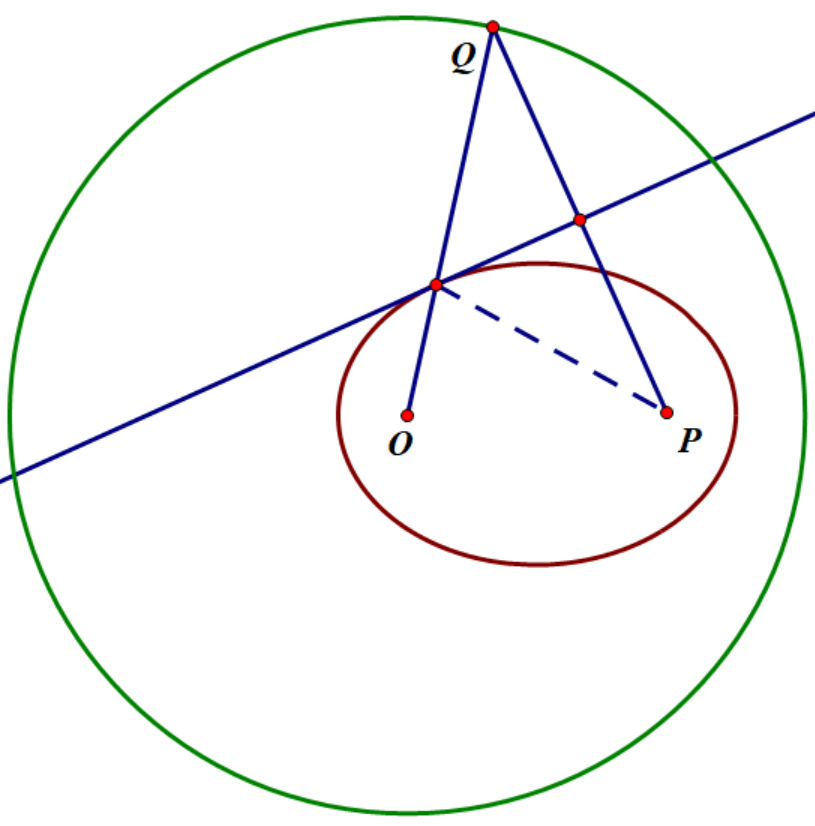
证明用到了将军饮马和椭圆上点到两焦点距离和不变。
角动量守恒定律、作用在行星上的引力直接指向太阳 作为前置知识。
我们先证明开二定律。
行星和太阳的连线在相等的时间间隔内扫过的面积相等。

在极短的时间 中,行星的轨迹看作直线,扫过的面积看作三角形(微积分状物)。
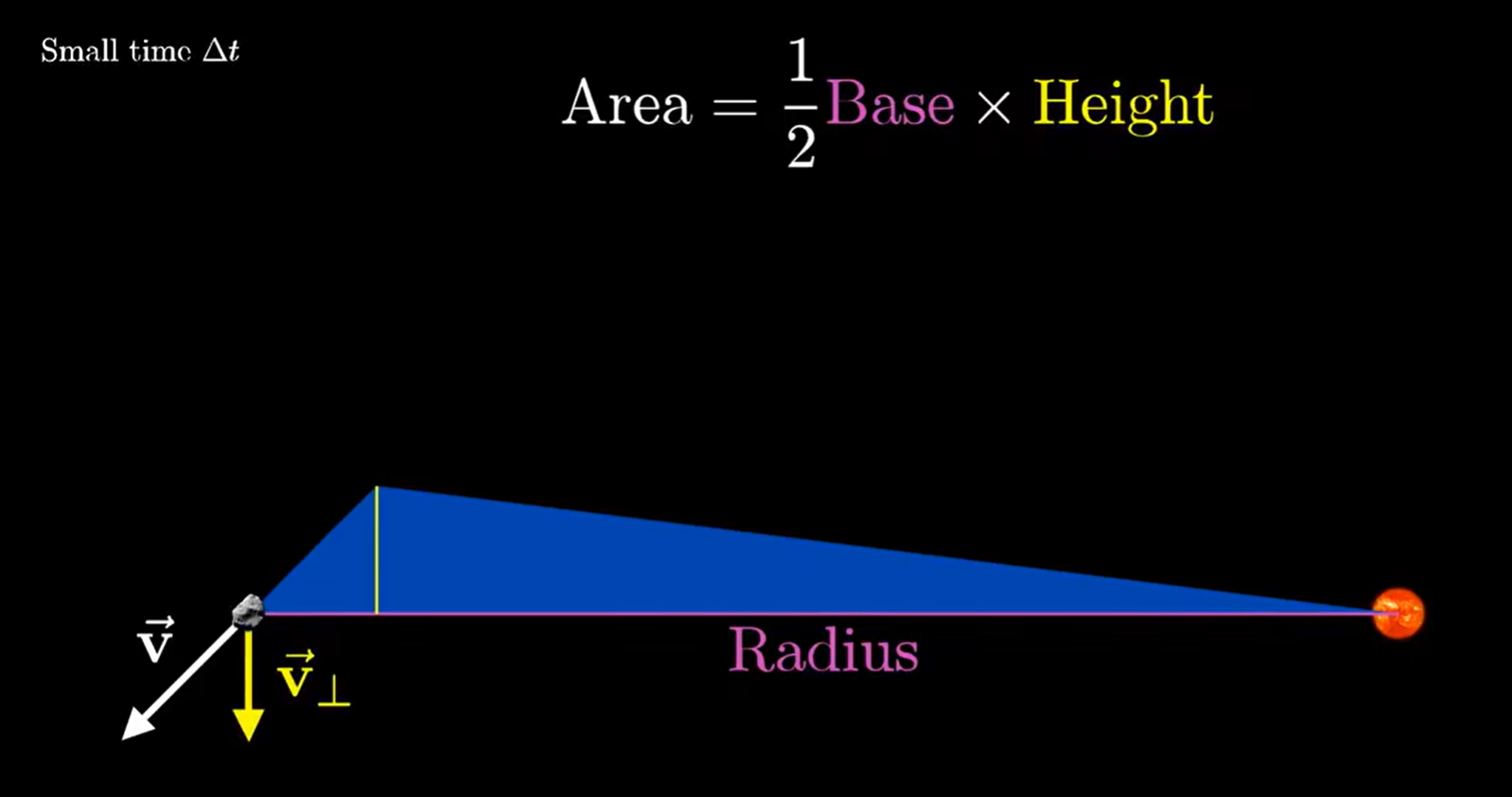
然后底乘高 算三角形面积。
由于太阳施加的引力总是指向太阳,行星质量不变,所以 为不变的常数。
然后我们就证完了,因为面积和时间成正比了。
(然而历史中开二才是推出角动量守恒的经验基础)
接着看开一:
所有行星绕太阳的轨道都是椭圆,太阳在椭圆的一个焦点上。
万有引力定律、牛顿第二定律 作为前置知识。
接下来讲的多数是我自创的 qwq。
我们将以太阳为中心,共 角度平均分为 个扇区(其实不是扇形),每份所属角度均为 。
注意这里 。
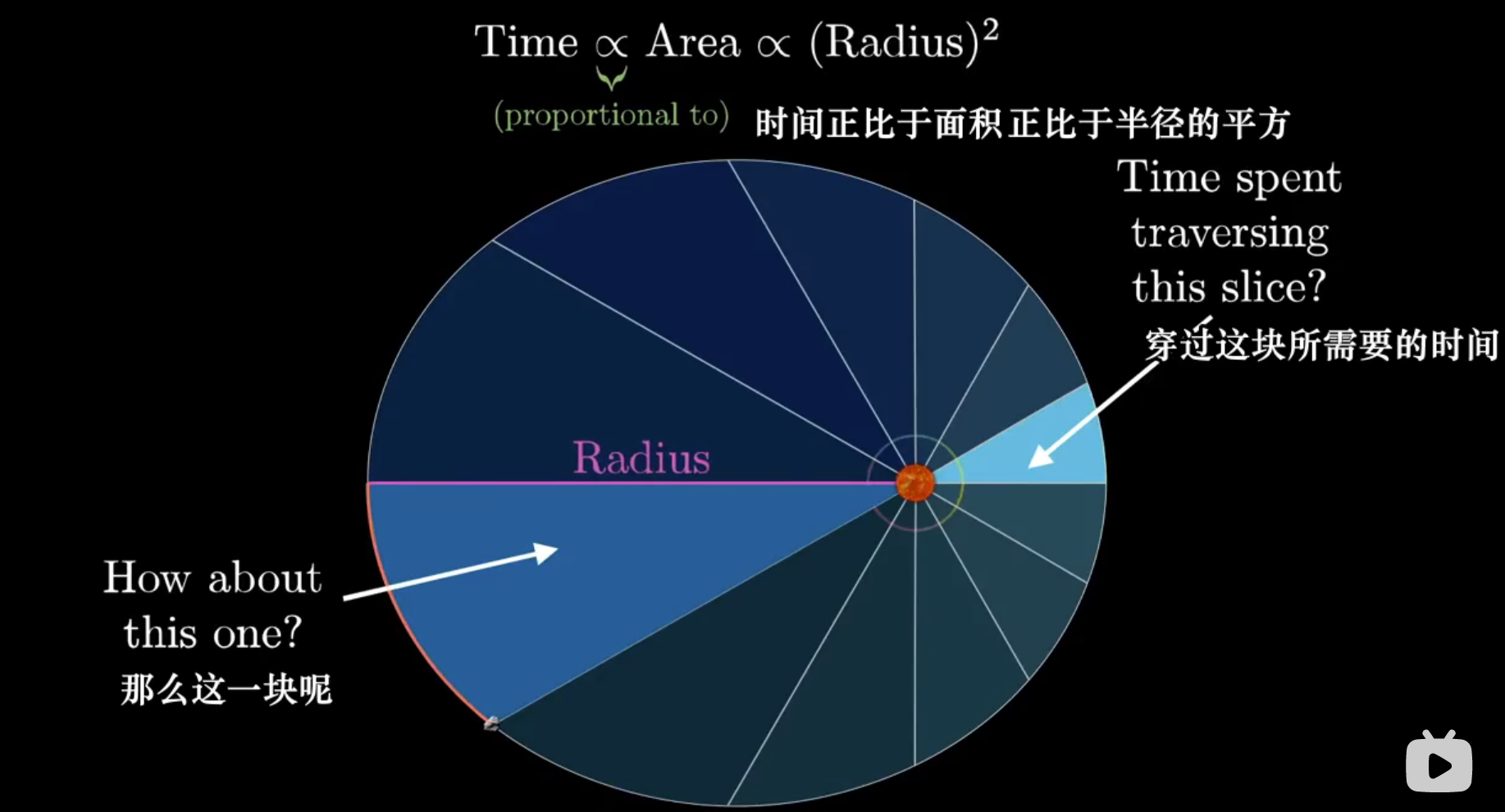
用我们刚刚证明的开二,得到经过一个扇区的时间正比于这个扇区的面积,而面积又正比于 (这里取哪个 是无关紧要的)。
行星每走完一个扇区我们就记录一下当前的速度向量,得到的是一个序列
循环差分一下得到新的一个序列
由于 ,我们 每一个元素在极限下必然指向太阳。
而 ,由于 正比于 ,而 由于万有引力定律正比于 ,所以 均相同。
然后做一遍前缀和状物,得到速度向量:

(自行脑部最后一根)
(黄色是 ,红蓝是 )
刚刚其实已经透露了, 的角度等差,所以我们最后做出来一个正多边形,极限看作是圆。
然后我们就得到了:在轨迹中角度为 的地方,速度向量为这个圆心角为 对应的偏心向量,这告诉了我们这个轨道上的点的切线方向。
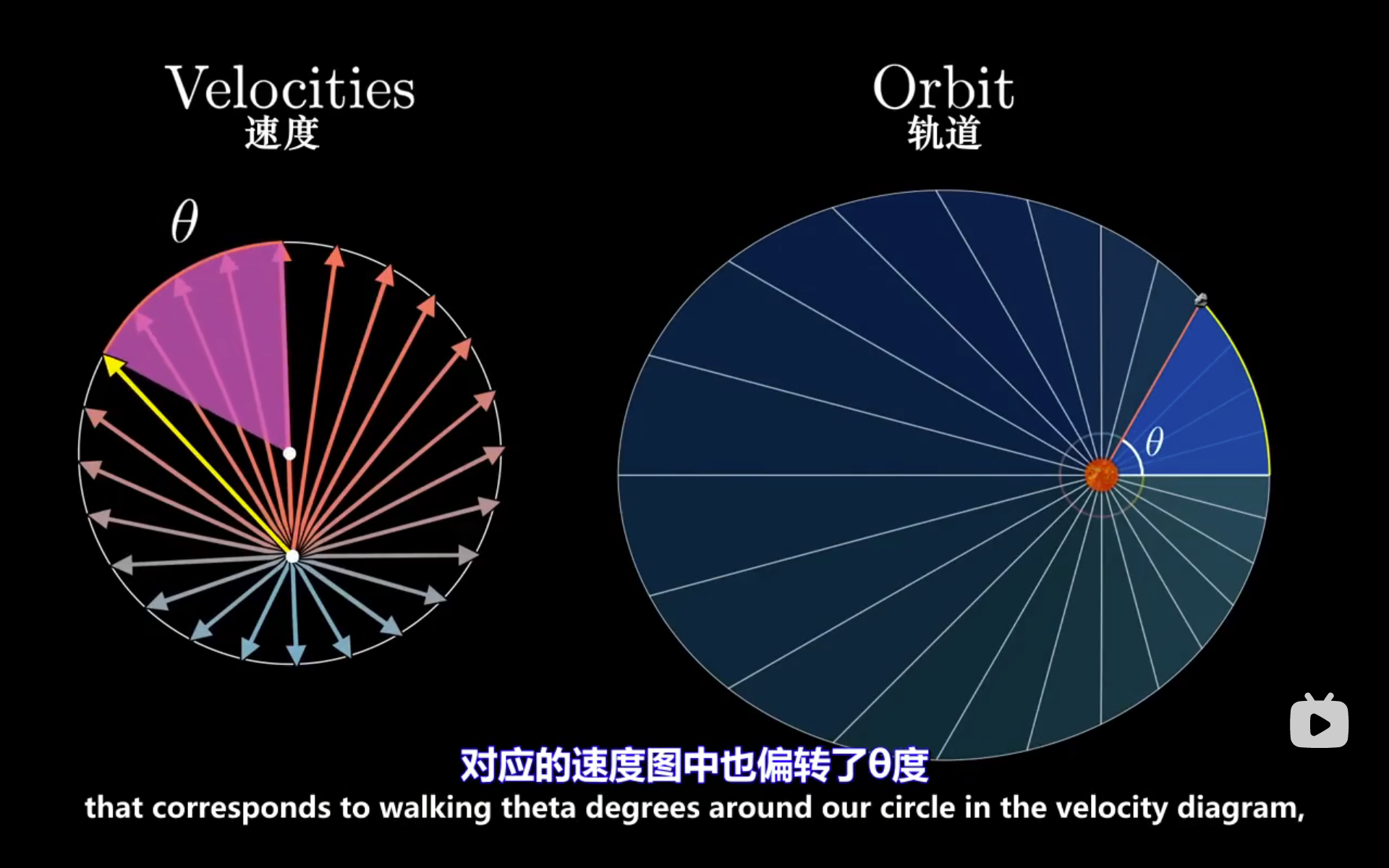
那么现在的问题就是:什么样的轨道满足这样的性质:
曲线与水平方向成 角的点上切线的方向,是由一个从圆内的一个特殊离心点到圆上垂直偏转 度的点连成的这个矢量所给定的。
(statement 很长,好好想想)
我们将左图顺时针旋转 。
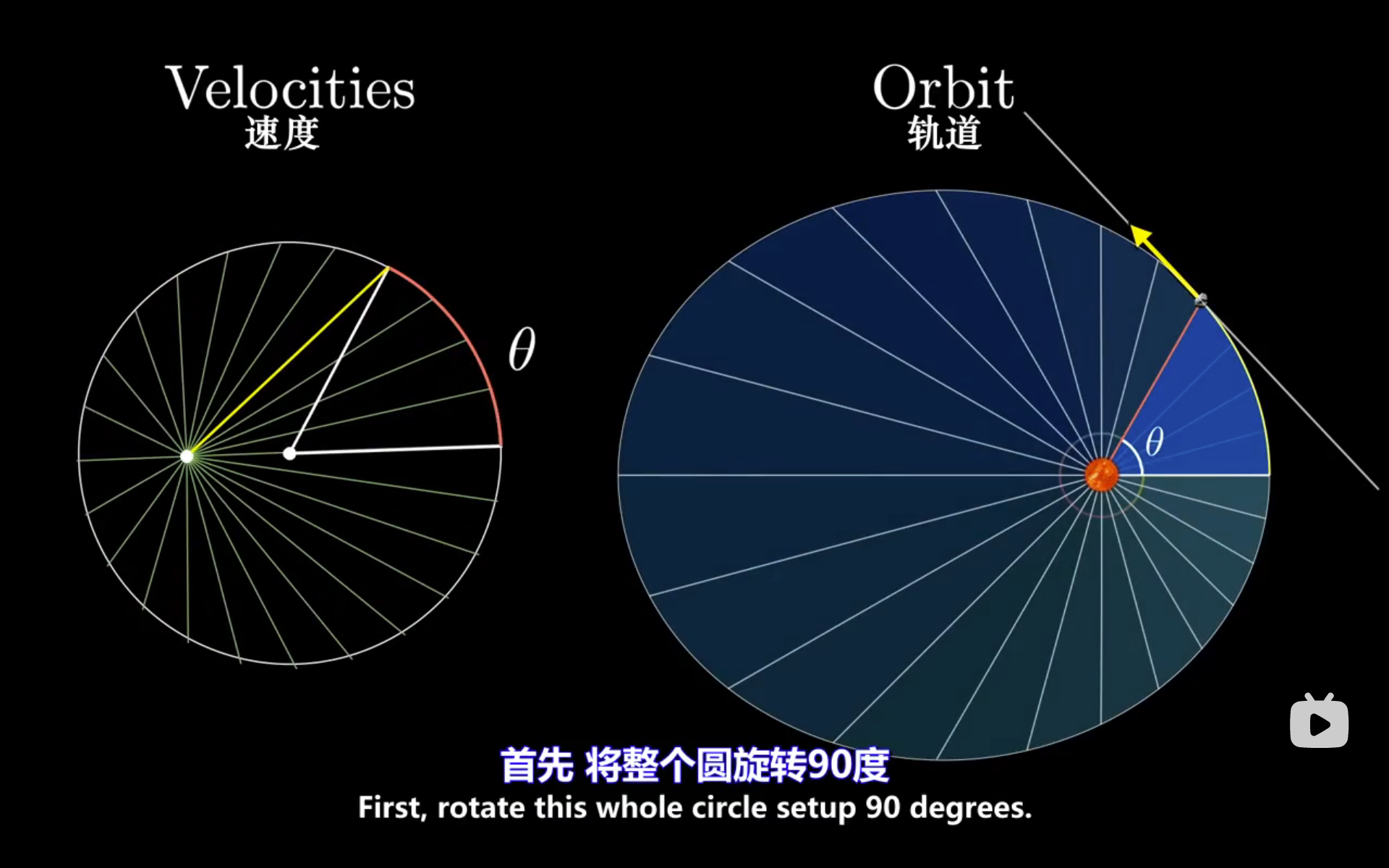
然后将这些速度向量逆时针旋转(中心旋转) 转回原来的角度。
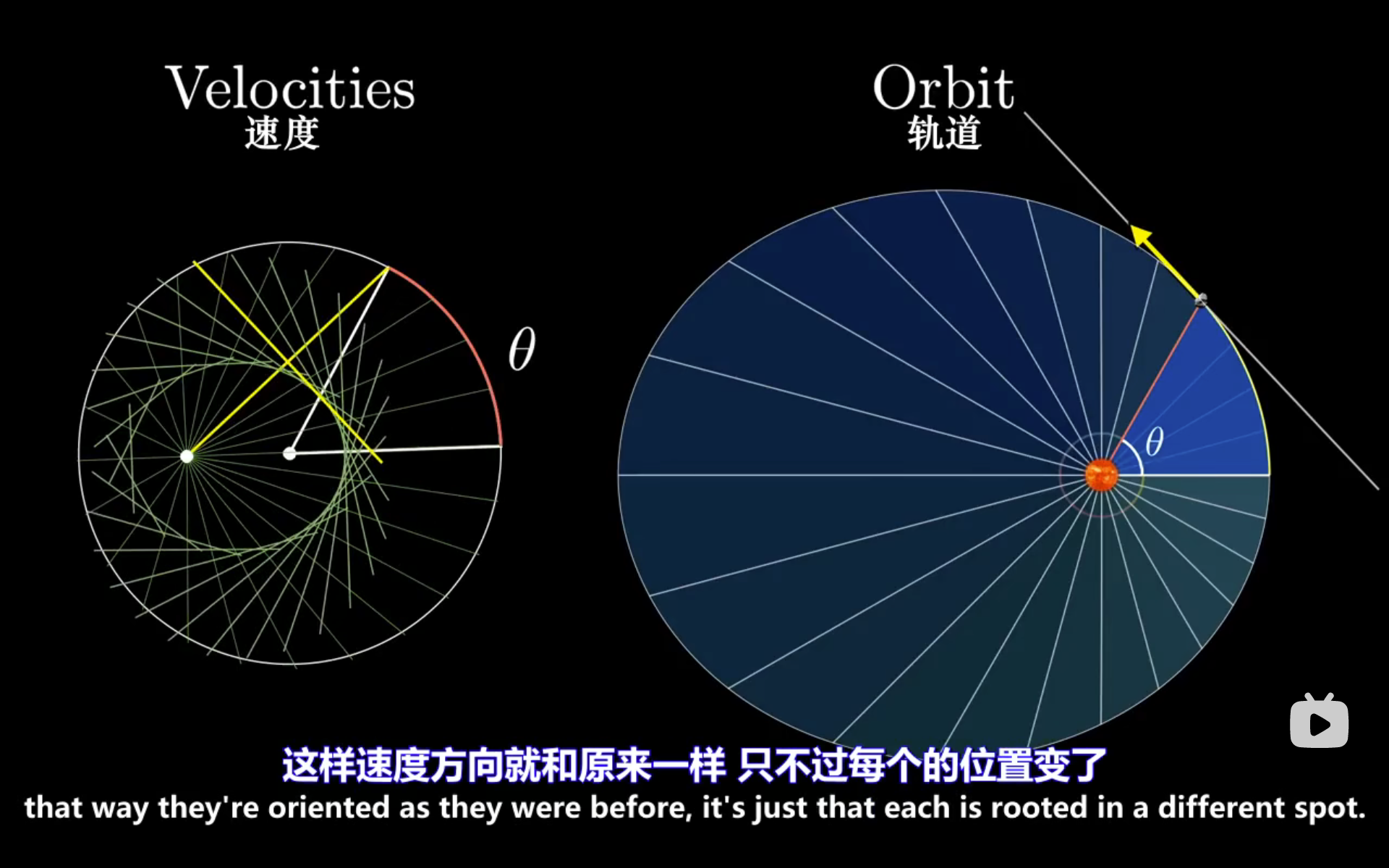
我们证明由无数直线切成的椭圆形相似于我们轨道。
回收伏笔了属实是。
重点在于,这条中垂线切于椭圆的点正好是交于半径的那个点(因为将军饮马,两点间线段最短)。
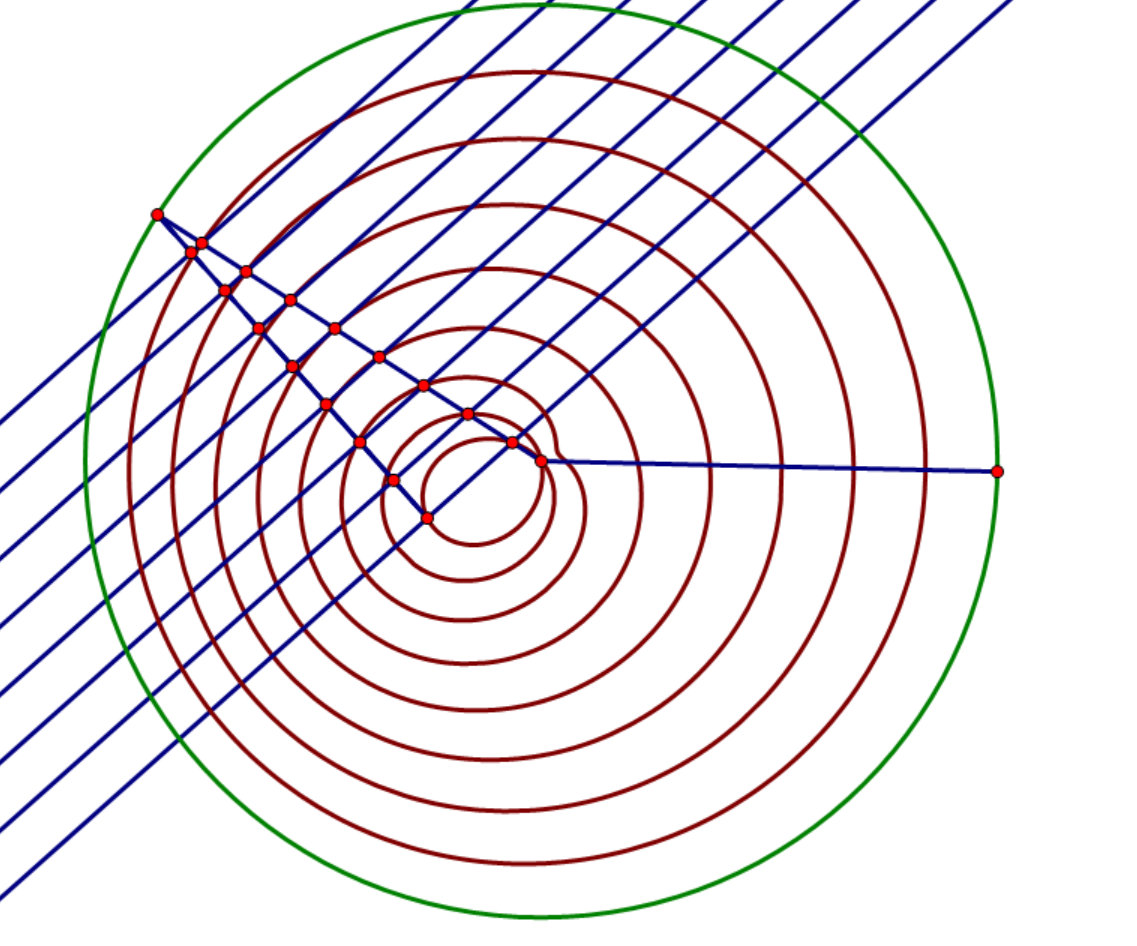
其实证明好像是有点问题的,因为如果非中心旋转在这些已知条件中好像也是合理的,所以不能判断一定为椭圆。
比如按 或 旋转,就明显不是椭圆。
因为我们没用到每个位置瞬时速度的大小这个条件。
问出去了。
好像不是这个渠道,算了摆。
本文来自博客园,作者:ShaoJia,版权归作者所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
2021-11-10 初学 二维树状数组
2021-11-10 FHQ Treap