圆周率,复平面,素数,高斯,共轭和积性函数
圆周率
我们都知道一个关于圆周率的公式:
这是莱布尼茨公式,他用微积分证明的,我们尝试用另一种方式来证明它。
复平面
我们最原始的想法是:找一个半径 尽量大的圆,放在单位正方形网格中,数有多少个格点被包含在这个圆内(接近于 ),以此来算出 的近似值。
数学里比较常见的是,当你看到和二维平面有关的问题时,就把这个平面看作全体复数的集合,再看问题或许会有意外收获。——3b1b
所以我们在复平面上考虑,一个半径足够大的圆(圆心定为 )内有多少格点。
我们枚举格点到圆心的距离,必然属于 (勾股)。
考察特定的距离 ,我们计算半径为 的圆会经过多少格点,将结果设为 ,则圆内的点数为
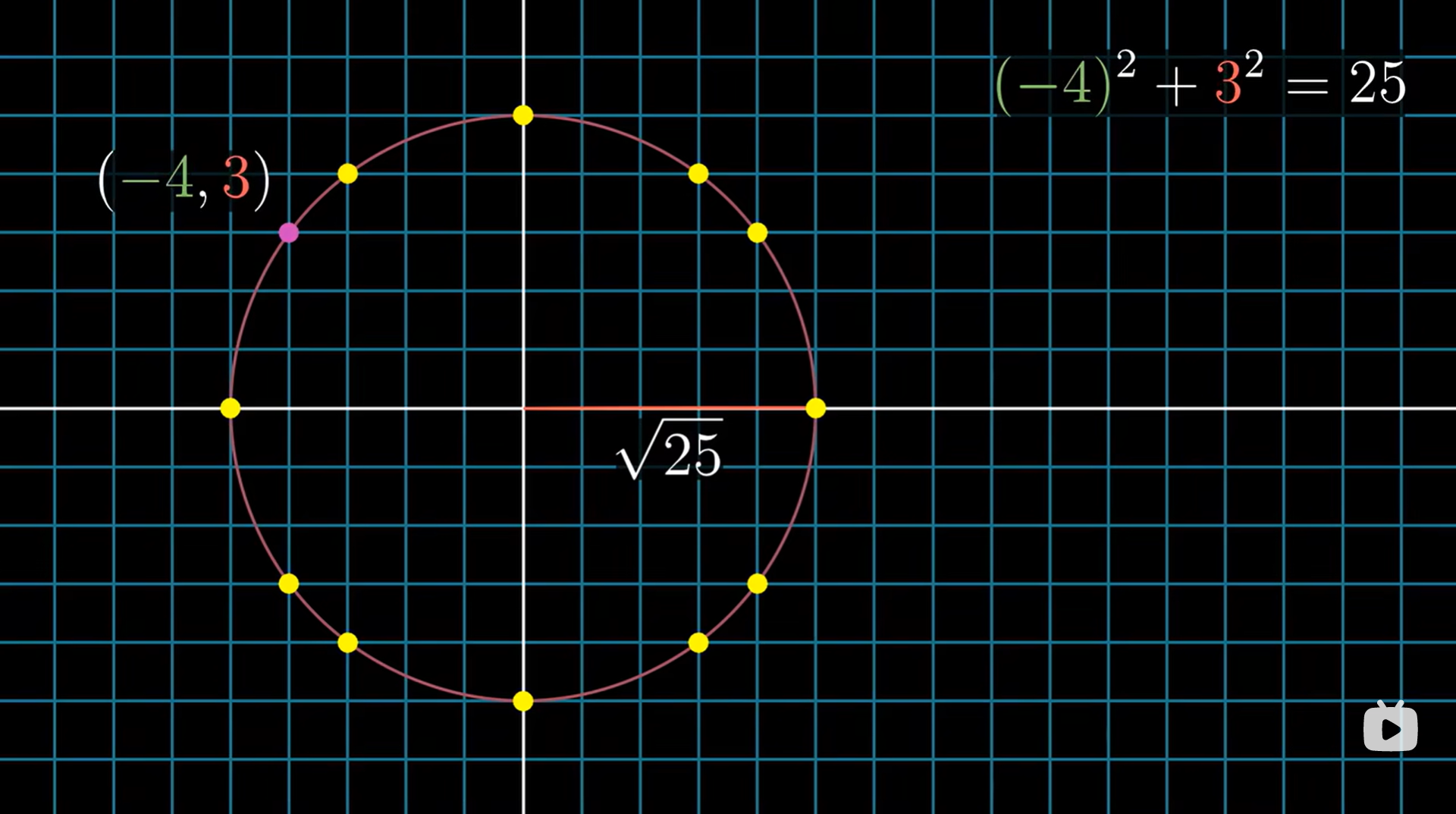
(上图 个点表示 )
那 咋求呢?
我们发现,相当于 的整数解个数(还是勾股)。
例如
以及每个数分别作相反数共 对数的平方和为 。
素数
接下来先扯一堆看起来离题的知识。
素数
emmm,不用多说。
唯一分解定理
也不用多说。
有时 这个因子要特判啥的。
高斯整数
实部和虚部都是整数的复数。
这个很好理解。
高斯素数
由于高斯整数形成了不可以转成有序环的欧几里德整环,所以是唯一因子分解整环。
相当于在高斯整数集中也有唯一分解定理。
那么不可或缺的就是在高斯整数集中的质元素,称为高斯素数。
高斯
注意,有些素数不是高斯素数,比如说 。
费马平方和定理:奇素数能表示为两个平方数之和的充分必要条件是该质数模 余 。
所以说,模 余 的奇素数是高斯素数,而对于模 余 的奇素数 :
不是高斯素数。
看上面的柿子,是否和我们刚刚留下的方程很像?
没错,我们留下的「 的整数解个数」相当于问:
分解成两个共轭的高斯整数的方案数。
共轭
复数 的共轭记为 。
共轭乘共轭还是共轭
复数、其倒数、其模长与其共轭的关系
平方差公式可证。
共轭的逆还是共轭的
通过上面的可以推导。
共轭除以共轭还是共轭
通过上面的可以推导。
一个高斯整数分解成两个共轭的高斯整数必然将所有共轭的因子都分在两边
反证法,若不是,则将所有分在两边的共轭均除掉,剩下的两边还是共轭。
设此时左边的集合为 ,右边为 。
我们记 表示将 中所有都变换为其共轭后的集合。
可知 和 元素乘积相等,且没有相同的元素,有背唯一分解定理,原命题得证。
↑ 证明过程非常不靠谱,请多指教。
积性函数
我们将 高斯素因数分解,每一对共轭的因子选择哪一个放在左边,而共轭不存在于此的因子我们必须将其平分在两侧。
所以,将 实数域上素因数分解后,模 余 的素数必须出现偶数次。
我们定义 函数,它是完全积性函数:
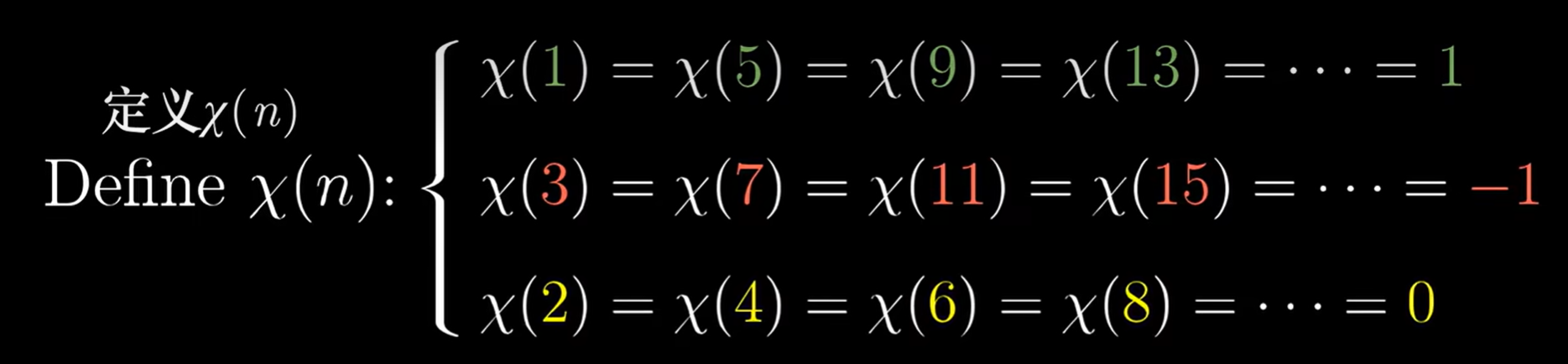
再结合 因子不影响分解数量, 因子会将最后的结果 (在复平面上转 的倍数),
我们终于得到 的高斯分解方案数了:
(模 余 的素数根据幂 震荡 ,模 余 的素数为幂次 ,代表有几种分配方案)
3b1b 翻译组原话:若一个只有实部的高斯素数幂次不是偶数,哦,那就完蛋了。
( 代表 )
(上述分解均在实数域内)
由于这是完全积性函数(积性其实就够了),上面的柿子可以简化为
最后的最后(柿子的所有化简均以 考虑):
再比较 ,得到
也就是
完结撒花!
结语
点击查看代码
//We'll be counting stars. #include<bits/stdc++.h> using namespace std; int ans=1,cnt,n; int calc(int p,int k){//sum of chi of same prime if(p%4==1) return k+1; else if(p%4==3) return (k&1)?0:1;//The 0 case cannot exist in this problem else return 1; } signed main(){ios::sync_with_stdio(false),cin.tie(nullptr); cin>>n;//n^2 prime factorization in fact. for(int i=2;i*i<=n;i++) if(n%i==0){ cnt=0; while(n%i==0) cnt++,n/=i; ans*=calc(i,2*cnt); } if(n>1) ans*=calc(n,2); cout<<4*ans<<endl;//dont forget to mul 4 return 0;}
恭喜你看了视频和 blog 后切了一道省选题。
本文来自博客园,作者:ShaoJia,版权归作者所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义