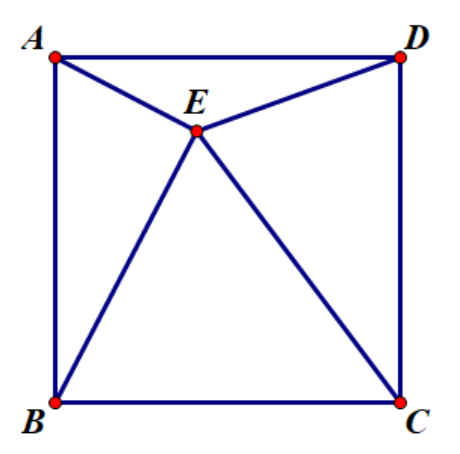
Q:AO⊥OB,AO=OB,CO⊥OD,CO=OD,BC⊥EF 求证 E 为 AD 中点
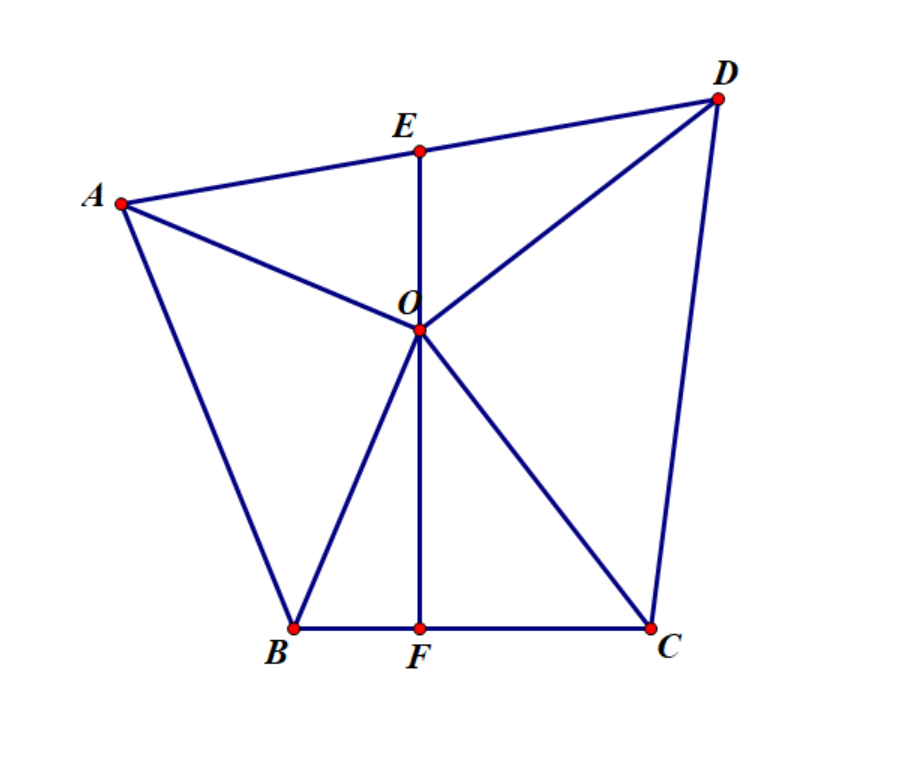
A:作如图 AI⊥IH⊥HD
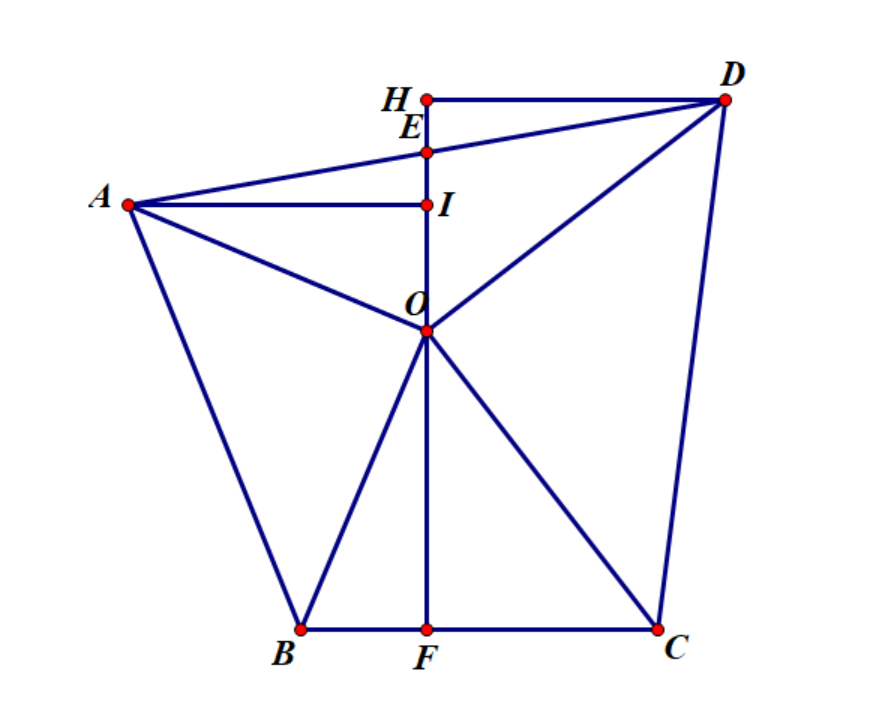
∵AO=OB,∠AIO=∠OFB,∠IAO=∠BOF
∴△AIO≅△BOF
∴AI=OF
同理可得 HD=OF=AI
∴△AIE≅△EHD
∴AE=ED 即 E 为 AD 中点
此题图中左右两侧均为三垂模型,可构造全等三角形
接下来一道包含内三垂和外三垂的题目:
Q:AB⊥AC,AB=AC,AD⊥AE,AD=AE,AF⊥FC 求证 G 为 BE 中点

A:作如图 BH⊥HI⊥IE
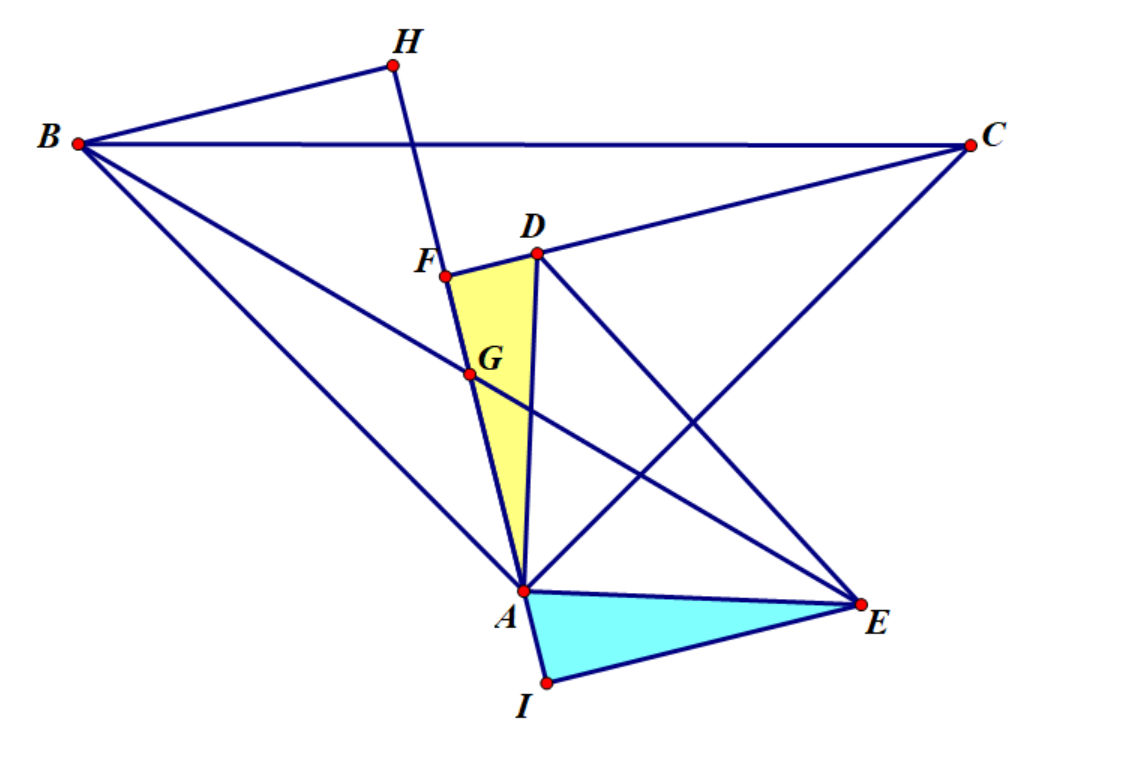
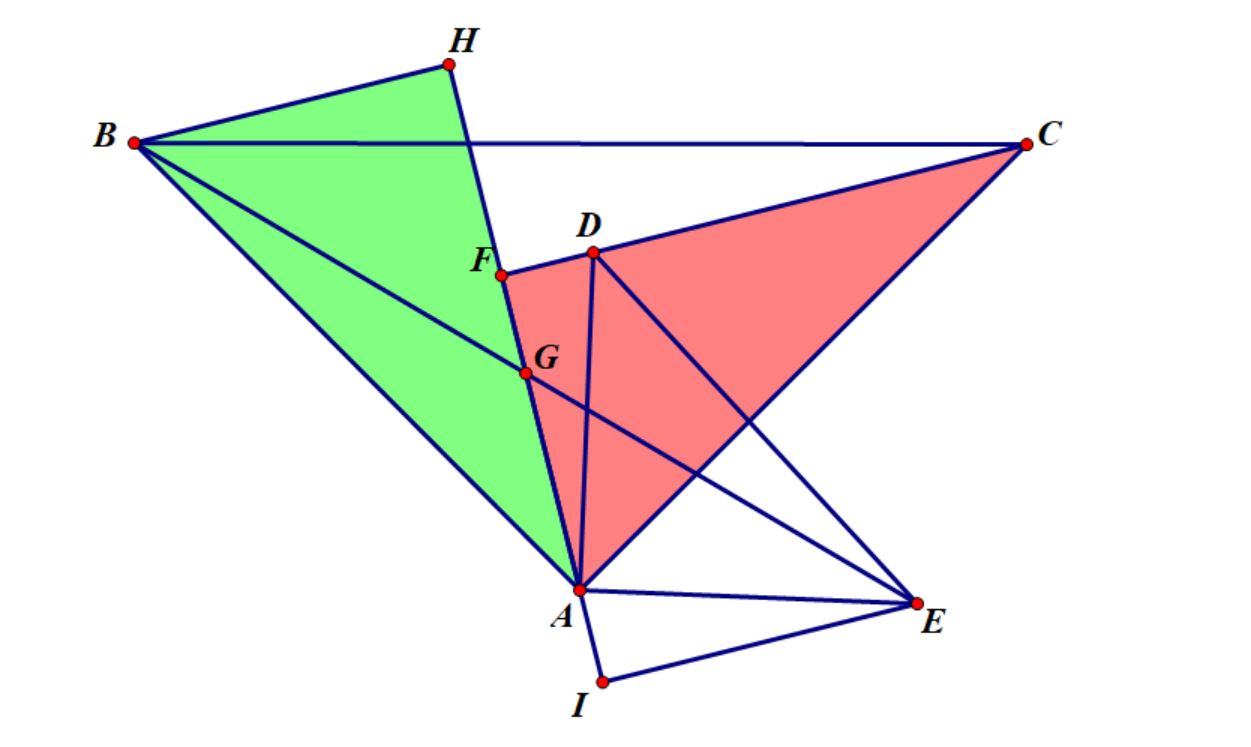
(为美观,过程已被删减)
∵△YELLOW≅△BLUE,△GREEN≅△RED
∴IE=AF=BH
∴△BHG≅△GIE
∴BG=GE 即 G 为 BE 中点
Q: □ABCD 中取一点 E 使 AE⊥EB,AE=1,CE=5 求DE的长
A:作如图

显然 △ABE≅△BCF≅△CDG≅△DAH
则 AE=BF=CG=DH=1
设 EF=FG=GH=HE=x
根据勾股定理
EF2+FC2=EC2
x2+(1+x)2=25
x1=3,x2=−4 ( x2 舍)
EH2+HD2=DE2
x2+1=DE2
DE2=10
DE=√10
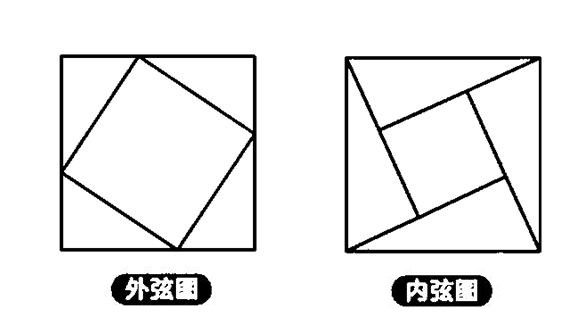
此类图称为正方形的内弦图
正方形的弦图为多个三垂模型叠加而来
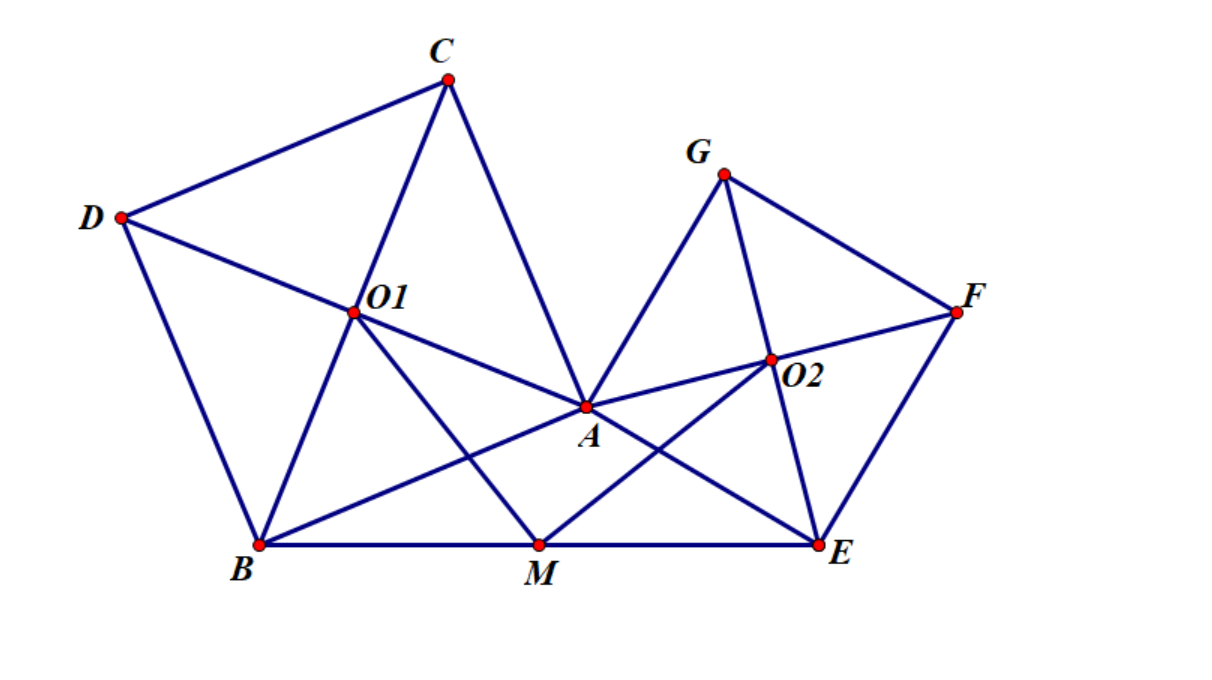
Q:如图,O1,O2分别为两个正方形的中心点,M是BE的中点,求证MO1=MO2,MO1⊥MO2
A1:(jio拉jio模型:手拉手变式)如图,倍长O2M至H
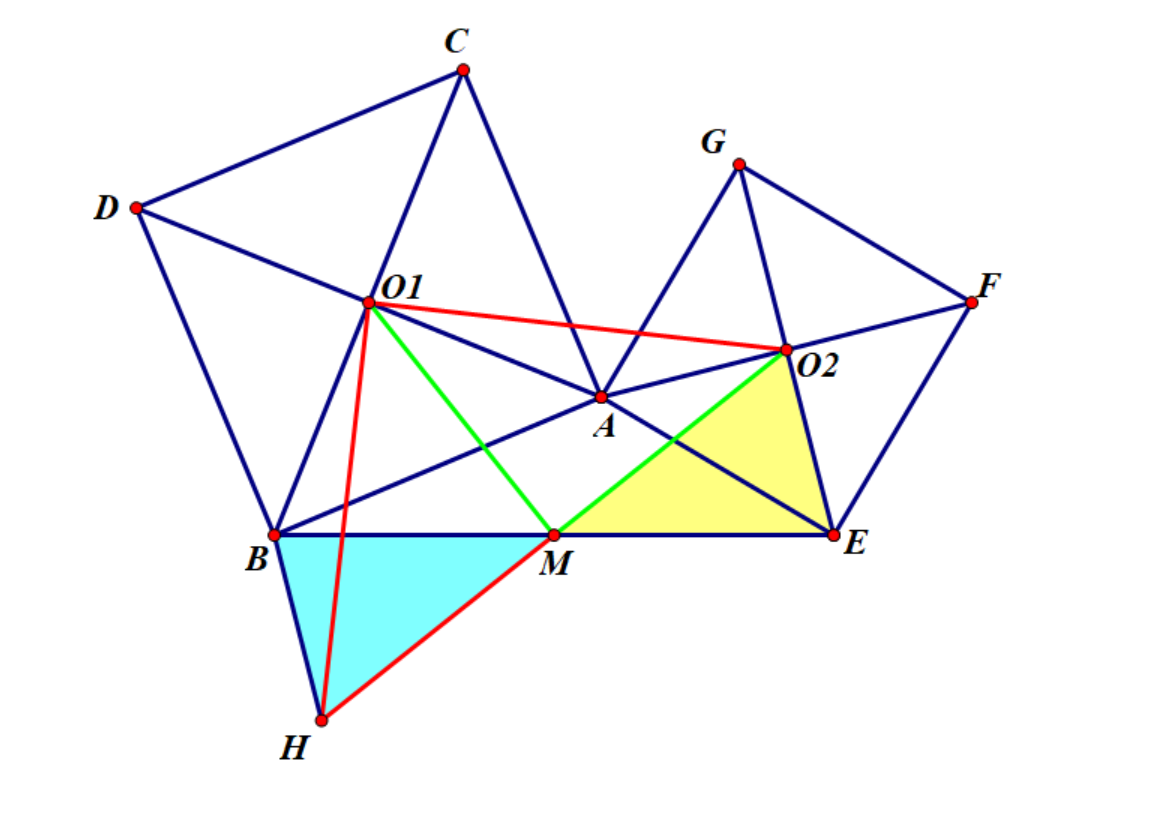
显然△O2EM≅△BHM
AO2=O2E=BH,AO1=O1B
(导角过程略)∠HBO1=∠O1AO2
△HBO1≅△O1AO2
∠HO1O2=∠BO1A=90∘,HO1=HO2(等腰直角三角形)
MO1=MO2,MO1⊥MO2
A2:(三角形中位线)连接 CE,BG 则 CE=2MO1,GB=2MO2
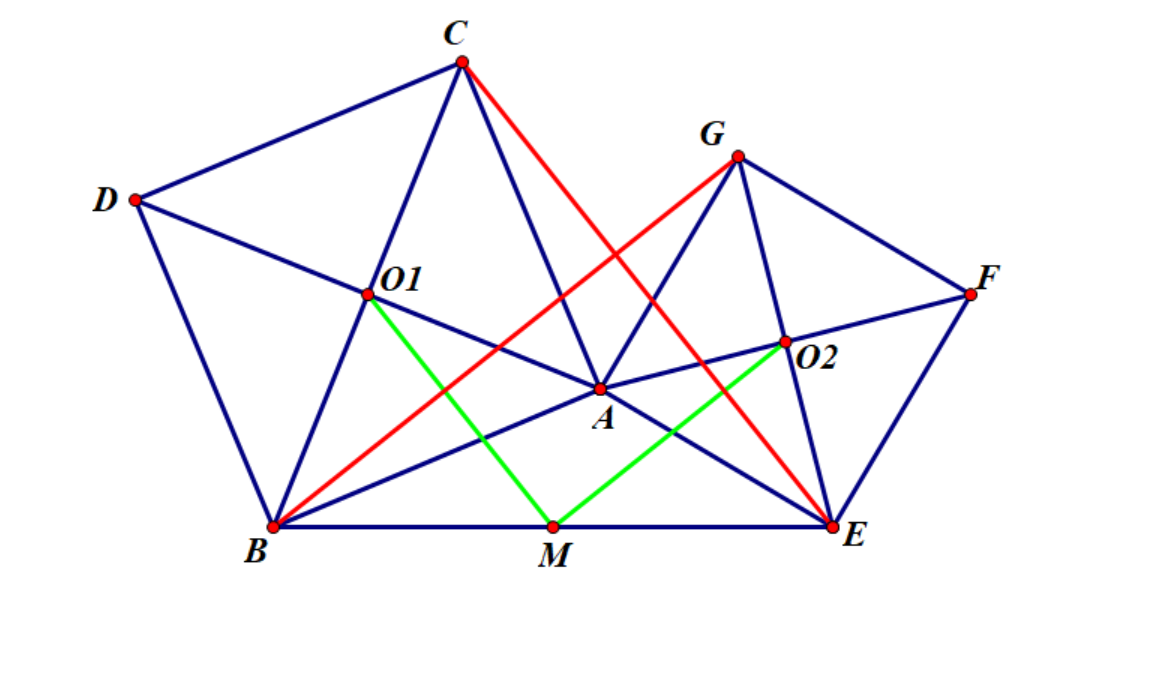
∵△BAG≅△CAE(证明略)
∴CE=BG,CE⊥BG(证明略)
∴MO1=MO2,MO1⊥MO2














【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义