信用评分卡模型的理论准备

0 前言

评分卡模型最早是用在银行审批用户申请贷款的环节。不过，由于近年来小贷的盛行，越来越多的公司开始基于自己平台的用户数据来构建评分卡模型。银行信用评分卡一般分为两类：

1. 申请评分卡，对新贷款申请进行筛选并判断其违约风险；
2. 行为评分卡，对审批通过的贷款账户进行覆盖整个贷款周期的管理。

在介绍评分卡的构建过程之前，我们首先引入一个标准信用卡的格式示例，这样可以有一个直观的概念。

其中，485 是模型计算的基础分值，39，36，38 分别是 Age，TAR，ES 变量取值所在评分区间或类型的得分，将它们相加就得到了该用户在所建评分卡的最后总得分。

本篇文章主要介绍评分卡构建中的几个主要概念，以及在构建评分卡过程中遇见的些许问题，目的也是为了方便自己日后查阅。对于样本的数据处理过程和代码实现并没有涉及。

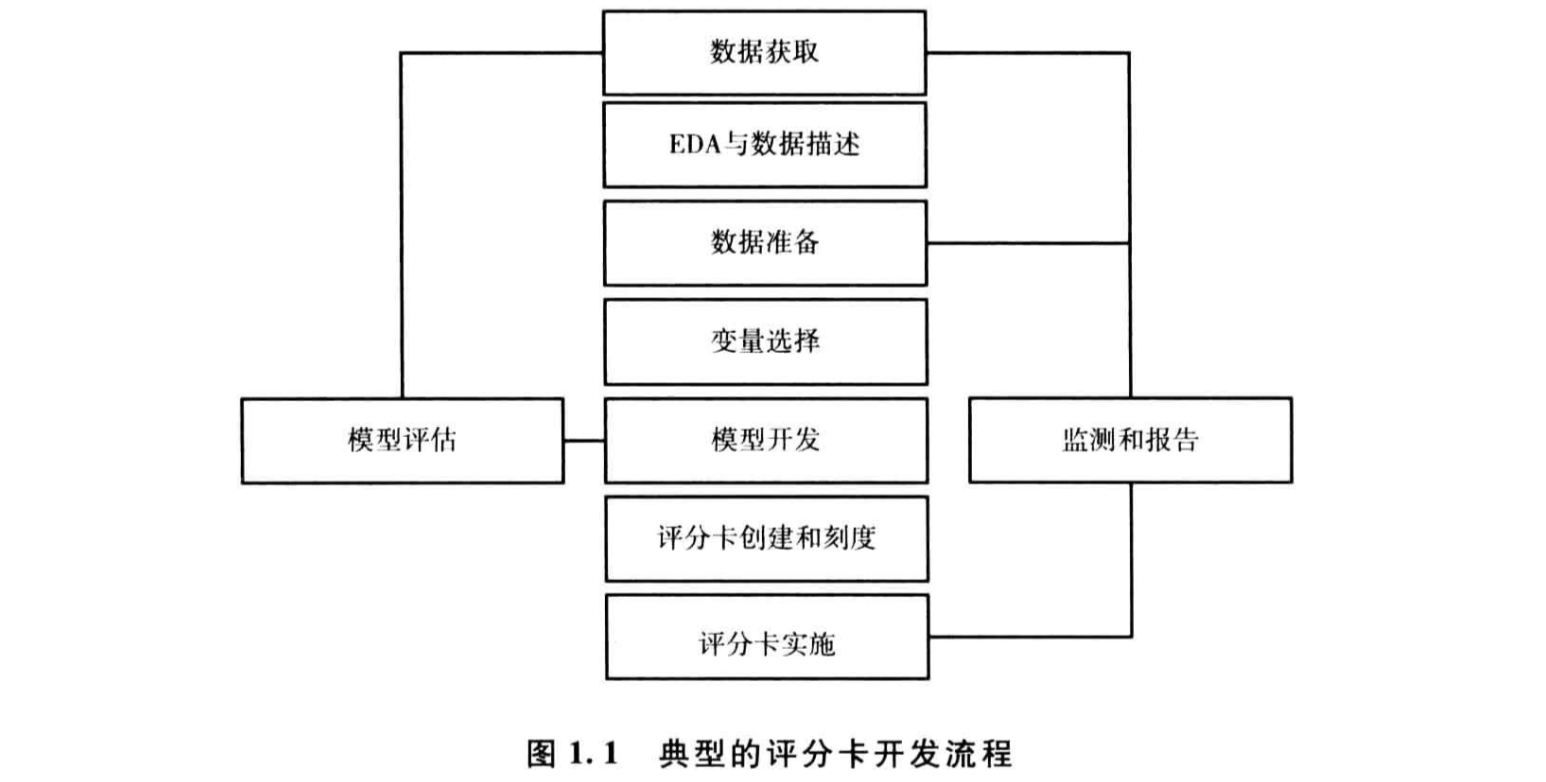
1 构建评分卡的整个流程图

该流程中各个步骤的顺序可以根据具体情况的不同进行调整，也可以根据需要重复某些步骤。

2 信息值 IV（Information Value）和 证据权重 WOE（Weight of Evidence）

2.1 WOE 定义

介绍 IV 的计算方法之前，首先要明白 WOE 的概念，因为 WOE 是计算 IV 的基础。标准评分卡的创建也可以不采用 WOE 转换，引入 WOE 的目的也不是为了提高模型质量。

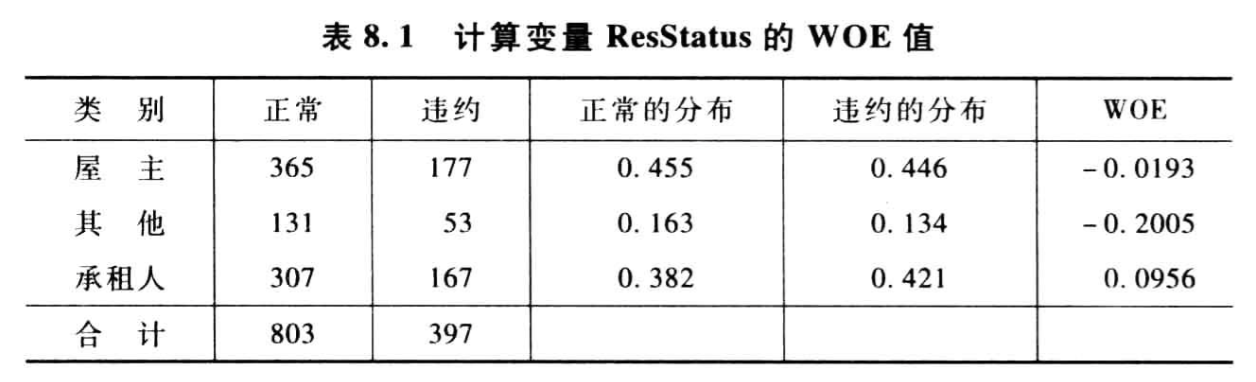
如上，变量 ResStatus 为类别变量，有三种类别：屋主、其他、承租人。表中计算了这个变量的每种类别对应目标变量所占的正常和违约的人数，正常占全部正常的比例（正常的分布）和违约占所有违约的比例（违约的分布），然后计算每个类别对应的 WOE 。

WOE 的定义如下：

\[WOE_i = \ln \left[ \frac{Bad\ Distribution_i}{Good\ Distribution_i} \right] \]

或

\[WOE_i = \ln \left( \frac{B_i / B_T}{G_i / G_T} \right) \]

其中\(B_i, B_T, G_i, G_T\) 分别为第 \(i\) 类中违约用户数量、总的违约用户数量、第 \(i\) 类中正常用户数量、总的正常用户数量。

需要记住的是，对于类别 \(i\)，正常和违约的分布分别定义为：

\[Good\ Distribution_i = \frac{Number\ of\ Good_i}{Total\ Number\ of\ Good} \]

和

\[Bad\ Distribution_i = \frac{Number\ of\ Bad_i}{Total\ Number\ of\ Bad} \]

如果括号内的比值小于 1， WOE 为负值；反之为正值。上面表中 ResStatus 变量为类别型变量，同样的定义和计算方法也适用于连续型变量，但对于连续型变量计算 WOE 之前，需要先将变量分段（bin）。

从上式中可以发现，\(WOE_i\) 为第 \(i\) 类中违约与正常的比率与整个样本中违约与正常比率的比值的对数。因此，其目的是衡量第 \(i\) 类对违约与正常的比率的影响程度。\(|WOE_i|\) 越大，说明此类别更能区分违约与正常用户，\(|WOE_i|\) 越小，此类别区分违约与正常不明显。

通常，对连续型变量进行分箱计算 WOE 之后，其各个分箱的 WOE 值应该呈现一个单调趋势。当然，有时连续性变量的 WOE 也有可能呈现一个 U 型趋势（比如在上面前言中评分卡的变量 Age）。不管如何，首先都要从业务上能给出一个合理的解释，否则，这个变量很可能没法放到我们最后创建的评分卡中。

2.2 IV 定义

IV 是用来衡量自变量对目标变量的影响程度的指标。

\[IV_i = (B_i / B_T - G_i /G_T) * \ln ( \frac{B_i / B_T}{G_i / G_T} ) \]

\[IV = \sum_i IV_i \]

IV 值是 WOE 的加权求和，在 \(IV_i\) 的表达式中分为两个部分，可以认为，前一部分表示此分组在全部数据中所占比例，后一部分则表示此分组区分违约与正常用户的能力。\(IV_i\) 由两部分的值共同决定，也就决定了最后的 \(IV\)。

2.3 IV 的极端情况

IV 依赖 WOE，如果在分箱后的某个分组对应的违约或者正常的用户数为 0，则这个分组对应 \(WOE_i = \infty\) ，相应的 \(IV_i = +\infty\) ，而此时这样分组是没有意义的。解决方法如下：

1. 如果此分组在所有样本中所占比例比较大，则可考虑将此变量的分组单独作为一条规则，作为模型的前置条件或补充条件；
2. 如果此分组在所有样本中所占比例比较小，可重新对变量进行分组，使这种现象不再发生；
3. 可以将分组中的数据 0 用 1 代替，使计算有意义。

3 评分卡构建

3.1 评分卡刻度

对于任意一个用户，将其被估计的违约概率表示为 \(p\)，则估计的正常概率为 \(1-p\)，则可以得到：

\[Odds = \frac{p}{1-p} \]

评分卡设定的分值刻度可以通过将分值表示为 Odds 对数的线性表达式来定义。如下表示：

\[Score = A - Blog(Odds) \]

其中，A 和 B 为常数。上式中负号可以使得违约概率越低，得分越高。
Logistic 回归模型计算 Odds 如下：

\[log(Odds) = \beta_0 + \beta_1x_1 + \cdots + \beta_px_p \]

其中，\(\beta_0, \beta_1, \cdots, \beta_p\) 由 Logistic 模型拟合给出。

常数 A 和 B 通常被称为补偿和刻度，它们的值可以通过将两个已知或者假设的分值带入 $ Score = A - Blog(Odds) $ 中得到。通常，需要两个假设：

• 在某个特定的比率设定特定的预期分值 \(P_0\);
• 指定比率翻番的分数（PDO，Point-to-Double Odds）。

首先，设定比率为 \(\theta_0\) 的特定点的分值为 \(P_0\)。然后，比率为 \(2\theta_0\) 的点分值为 \(P_0 - PDO\)。带入得到两个等式：

\[P_0 = A - Blog(\theta_0) \]

\[P_0 - PDO = A - Blog(2\theta_0) \]

解上述两个方程中的常数 A 和 B, 可以得到：

\[B = \frac{PDO}{log(2)} \]

\[A = P_0 + Blog(\theta_0) \]

例如，假设想要设定评分卡刻度使得比率为 1:60（违约与正常）时的分值为 600 分，PDO = 20。然后计算出 B = 28.85， A = 481.89，于是计算得分公式为：

\[Score = 481.89 - 28.85log(Odds) \]

3.2 基于 Logistic 的评分卡构建

最终，评分卡的分值可以写成下列形式：

\[Score = A - B(\beta_0 + \beta_1x_1 + \cdots + \beta_px_p) \]

变量 $ x_1, \cdots, x_p $ 为自变量对应 WOE，可以进一步写成：

\[ Score = A - B\left\{ \begin{array}{c} \beta_0 \\ + (\beta_1\omega_{11})\delta_{11} + (\beta_1\omega_{12})\delta_{12} + \cdots \\ \cdots \\ + (\beta_p\omega_{p1})\delta_{p1} + (\beta_p\omega_{p2})\delta_{p2} + \cdots \end{array} \right\} \]

其中，\(\omega_{ij}\) 是第 \(i\) 个变量对应的第 \(j\) 个类别上的 WOE , \(\delta_{ij}\) 是二元变量，表示变量 \(i\) 是否取第 \(j\) 个值。 上式可重新写为：

\[ \begin{array}{lr} Score = (A - B\beta_0) \\ - (B\beta_1\omega_{11})\delta_{11} - (B\beta_1\omega_{12})\delta_{12} - \cdots \\ - \cdots \\ - (B\beta_p\omega_{p1})\delta_{p1} - (B\beta_p\omega_{p2})\delta_{p2} - \cdots \end{array} \]

其中，\(A - B\beta_0\) 为基础分值，而下面每一行对应的相应变量 \(x_1, \cdots, x_p\) 的得分。

3.3 其它算法评分卡构建

从上面可以看到，基于 Logistic 的评分卡给予每个变量的每个分箱一个特定的分数，其目的是对评分卡做出一个合理的解释，例如，如果客户想提高自己的评分，可以通过提高评分卡中的某些指标的值，使之对应的分数提高就可以了。

当然，还有其它一些算法可以帮助我们构建评分卡，比如：RandomForest， GBDT 等。这些算法可以给出客户的违约概率，但是构建的评分卡不能像 Logistic 那样计算每个变量的分箱或类型得分，我们只能根据这个违约概率计算客户的总评分。但依然要依据上面定义的评分刻度：

\[Score = A - Blog(Odds) \]

其中，

\[Odds = \frac{p}{1-p} \]

4 模型稳定性 PSI（Population Stability Index）

4.1 稳定性监测

模型上线之后，要对实际运行情况进行监测，主要为两个方面：

用户在模型中得分分布的稳定性：模型上线之后的真实数据得分分布（real data）和建模时训练数据（train data）的得分分布比较；

变量稳定性：模型上线之后的实际变量分布（real data）和建模时训练数据分布（train data）比较。

4.2 PSI 计算

首先对样本 A 和样本 B 得分按照同一标准分为几个区间（类别型变量按类别分），计算样本在每个区间上的占比。在每个区间上，将两个样本各自占比相除再取对数，然后乘以各自占比之差，最后将各个区间的计算值相加，最终得到 PSI（类似于IV计算），如下：

\[PSI = \sum_i (A_i / A_T - B_i /B_T) * \ln ( \frac{A_i /A_T}{B_i / B_T} ) \]

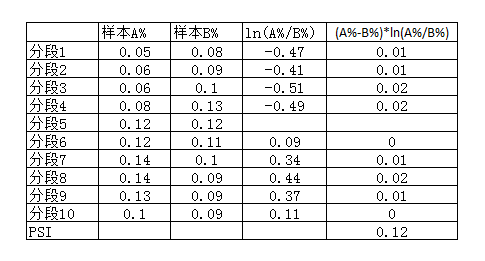
• PSI < 0.1 样本分布有微小变化
• PSI 在 0.1 和 0.2 之间， 样本分布有变化
• PSI > 0.2 样本分布有显著变化

重点关注 PSI > 0.2 的变量，说明此变量的分布在建模时与现在已经发生了显著的变化，查找 PSI 变动的原因，并重新调整模型。

参考资料

1. 《信用风险评分卡研究——基于SAS的开发与实施》
2. 数据挖掘模型中的IV和WOE详解
3. 评分卡上线后如何进行评分卡的监测