EM 算法和高斯混合模型

EM 算法是一种迭代算法，1977 年由 Dempster 等人总结提出，用于含隐变量（hidden variable）的概率模型参数的极大似然估计，或极大后验概率估计。EM 算法的每次迭代由两步组成：E 步，求期望（expectation）; M 步，求极大（maximization）。所以这一算法称为期望极大算法（expectation maximization algorithm），简称 EM 算法。

1 EM 算法

1.1 预备知识

（1） 观测变量和隐变量
概率模型有时候既含有观测变量（observable variable），又含有隐变量或潜在变量（latent variable）。如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计法，或贝叶斯估计法估计模型参数。但是，当模型含有隐变量时，就不能简单地使用这些估计方法。

（2）完全数据和不完全数据
用 \(Y\) 表示观测随机变量的数据，\(Z\) 表示隐随机变量的数据。\(Y\) 和 \(Z\) 连在一起成为完全数据（complete-data），观测数据 \(Y\) 又称为不完全数据（incomplete-data）。假设给定观测数据 \(Y\)，其概率分布是 \(P(Y|\theta)\)，其中 \(\theta\) 是需要估计的模型参数，那么不完全数据 \(Y\) 的似然函数是 \(P(Y|\theta)\)，对数似然函数 \(L(\theta) = \log P(Y|\theta)\)；假设 \(Y\) 和 \(Z\) 的联合概率分布是 \(P(Y, Z|\theta)\)，那么完全数据的对数似然函数是 \(\log P(Y, Z|\theta)\)。EM 算法通过迭代求 \(L(\theta) = \log P(Y|\theta)\) 的极大似然估计。每次迭代包含两步：E 步：求期望；M 步，求极大化。

（3）Jensen 不等式

当 \(f(x)\) 为凸函数（这里指下凸函数，有的教材凹凸的定义不同）时，有Jensen 不等式（也称詹森不等式、琴生不等式），

\[f(E[x]) \le E[f(x)] \]

可以作一个很直观的解释（如下图），比如说在二维空间上，凸函数是一个开口向上的抛物线，假如我们有两个点 \(a, b\)，那么 \(f(E[x])\) 表示的是两个点的均值的纵坐标，而 \(E[f(x)]\) 表示的是两个点纵坐标的均值。

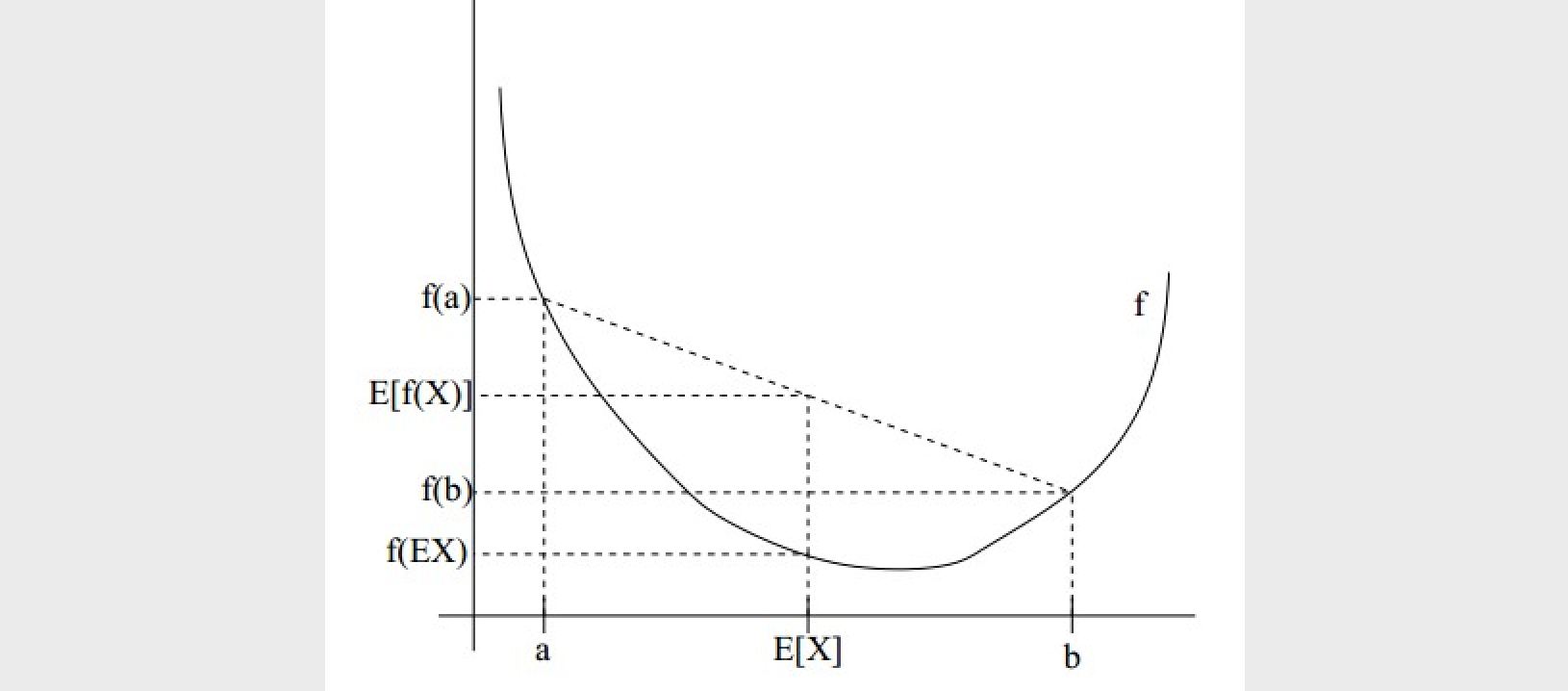
当函数 \(f(x)\) 为对数函数（\(\log\)，为凹函数，或上凸函数）时，上面的公式刚好反过来，即

\[f(E[x]) \ge E[f(x)] \]

1.2 EM 算法的引入

例（三硬币模型） \(\quad\) 假设有 3 枚硬币，分别记作 \(A, B, C\)。这些硬币正面出现的概率分别是 \(\pi, p, q\)。进行如下掷硬币实验：先掷硬币 \(A\)，根据其结果选出硬币 \(B\) 或硬币 \(C\)，正面选硬币 \(B\)，反面选硬币 \(C\)；然后掷选出的硬币，掷硬币的结果，出现正面记作 1，出现反面记作 0；独立地重复 \(n\) 次试验（这里，\(n=10\)），观测结果如下：

\[1, 1, 0, 1, 0, 0, 1, 0, 1, 1 \]

假设只能观测到掷硬币的结果，不能观测掷硬币的过程。问如何估计三硬币正面出现的概率，即三硬币模型的参数（\((\pi, p, q)\)）。

解 \(\quad\) 三硬币模型可以写作

\[\begin{aligned} P(y|\theta) & = \sum_z P(y, z|\theta) = \sum_z P(z|\theta)P(y|z, \theta) \\ & = \pi p^y(1-p)^{1-y} + (1-\pi)q^y(1-q)^{1-y} \end{aligned} \]

这里，随机变量 \(y\) 是观测变量，表示一次试验观测的结果是 1 或 0；随机变量 \(z\) 是隐变量，表示未观测到的掷硬币 \(A\) 的结果（正面或反面）；\(\theta = (\pi, p, q)\) 是模型参数。这一模型是以上数据的生成模型。注意，随机变量 \(y\) 的数据可以观测，随机变量 \(z\) 的数据不可观测。

将观测数据表示为 \(Y=(Y_1, Y_2, \cdots, Y_n)^T\)，未观测数据表示为 \(Z=(Z_1, Z_2, \cdots, Z_n)^T\)，则观测数据的似然函数为

\[P(Y|\theta) = \sum_Z P(Z|\theta)P(Y|Z, \theta) \]

即

\[P(Y|\theta) = \prod_{j=1}^{n} \pi p^{y_j}(1-p)^{1-y_j} + (1-\pi)q^{y_j}(1-q)^{1-y_j} \]

考虑求模型参数 \(\theta = (\pi, p, q)\) 的极大似然估计，即

\[\hat{\theta} = \arg \max \limits_{\theta} \log P(Y|\theta) \]

这个问题没有解析解，只有通过迭代的方法求解。EM 算法就是可以用于求解这个问题的一种迭代算法。

1.3 算法（EM 算法）

EM 算法
输入：观测变量数据 \(Y\)，隐变量数据 \(Z\)，联合分布 \(P(Y, Z|\theta)\)，条件分布 \(P(Z|Y, \theta)\)；
输出：模型参数 \(\theta\)。

（1）选择参数初值 \(\theta^{(0)}\)，开始迭代；
（2）E 步：记 \(\theta^{(i)}\) 为第 \(i\) 次迭代参数 \(\theta\) 的估计值，在第 \(i+1\) 次迭代的 \(E\) 步，计算

\[\begin{aligned} Q(\theta, \theta^{(i)}) & = E_Z[\log P(Y, Z|\theta)|Y, \theta^{(i)}] \\ & = \sum_Z \log P(Y, Z|\theta)P(Z|Y, \theta^{(i)}) \end{aligned} \]

这里，\(P(Z|Y, \theta^{(i)})\) 是在给定观测数据 \(Y\) 和当前的参数估计 \(\theta^{(i)}\) 下隐变量数据 \(Z\) 的条件概率分布；

（3）M 步：求使 \(Q(\theta, \theta^{(i)})\) 极大化的 \(\theta\)，确定第 \(i+1\) 次迭代的参数的估计值 \(\theta^{(i+1)}\)

\[\theta^{(i+1)} = \arg \max \limits_{\theta}Q(\theta, \theta^{(i)}) \]

（4）重复第（2）和第（3）步，直到收敛。

上式的函数 \(Q(\theta, \theta^{(i)})\) 是 EM 算法的核心，称为 \(Q\) 函数（\(Q\) function）。

定义（Q 函数） \(\quad\) 完全数据的对数似然函数 \(\log P(Y, Z|\theta)\) 关于在给定观测数据 \(Y\) 和当前参数 \(\theta^{(i)}\) 下对未观测数据 \(Z\) 的条件概率分布 \(P(Z|Y, \theta^{(i)})\) 的期望称为 \(Q\) 函数，即

\[Q(\theta, \theta^{(i)}) = E_Z[\log P(Y, Z|\theta)|Y, \theta^{(i)}] \]

下面对 EM 算法作几点说明：
步骤（1）：参数的初值可以任意选择，但需注意 EM 算法对初值是敏感的。
步骤（2）：E 步求 \(Q(\theta, \theta^{(i)})\) 。\(Q\) 函数式中 \(Z\) 是未观测数据，\(Y\) 是观测数据。注意，\(Q(\theta, \theta^{(i)})\) 的第 1 个变元表示要极大化的参数，第 2 个变元表示参数的当前估计值。每次迭代实际在求 \(Q\) 函数及其极大。
步骤（3）：M 步求 \(Q(\theta, \theta^{(i)})\) 的极大化，得到 \(\theta^{(i+1)}\)，完成一次迭代 \(\theta^{(i)} \rightarrow \theta^{(i+1)}\)。后面将证明每次迭代使似然函数增大或达到局部极值。
步骤（4）：给出停止迭代的条件，一般是对较小的 \(\epsilon_1, \epsilon_2\)，若满足

\[||\theta^{(i+1)} - \theta^{(i)}|| < \epsilon_1 \quad或 \quad ||Q(\theta^{(i+1)}, \theta^{(i)}) - Q(\theta^{(i)}, \theta^{(i)})|| < \epsilon_2 \]

则停止迭代。

1.4 EM 算法的导出（\(Q(\theta, \theta^{(i)})\) 函数的由来）

面对一个含有隐变量的概率模型，目标是极大化观测数据（不完全数据）\(Y\) 关于参数 \(\theta\) 的对数似然函数，即极大化

\[\begin{aligned} L(\theta) &= \log P(Y|\theta) = \log\sum_Z P(Y, Z|\theta) \\ & = \log \big(\sum_Z P(Y|Z, \theta)P(Z|\theta) \big) \end{aligned} \]

这一极大化的主要困难是上式中有未观测数据并有包含和（或积分）的对数。

事实上，EM 算法是通过迭代逐步近似极大化 \(L(\theta)\) 的。假设在第 \(i\) 次迭代后 \(\theta\) 的估计值是 \(\theta^{(i)}\)。我们希望新估计值 \(\theta\) 能使 \(L(\theta)\) 增加，即 \(L(\theta) > L(\theta^{(i)})\)，并逐步达到极大值。为此，考虑两者的差：

\[L(\theta) - L(\theta^{(i)}) = \log \big( \sum_Z P(Y|Z, \theta)P(Z|\theta) \big) -\log P(Y|\theta^{(i)}) \]

利用 Jensen 不等式（Jensen inequality）得到其下界：

\[\begin{aligned} L(\theta) - L(\theta^{(i)}) & = \log \big( \sum_Z P(Z|Y, \theta^{(i)}) \frac{P(Y|Z, \theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)})} \big) -\log P(Y|\theta^{(i)}) \\ & \ge \sum_Z P(Z|Y, \theta^{(i)}) \log \frac{P(Y|Z, \theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)})} -\log P(Y|\theta^{(i)}) \\ & = \sum_Z P(Z|Y, \theta^{(i)}) \log \frac{P(Y|Z, \theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)}) P(Y|\theta^{(i)})} \end{aligned} \]

令

\[B(\theta, \theta^{(i)}) = L(\theta^{(i)}) + \sum_Z P(Z|Y, \theta^{(i)}) \log \frac{P(Y|Z, \theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)}) P(Y|\theta^{(i)})} \]

则

\[L(\theta) \ge B(\theta, \theta^{(i)}) \]

即函数 \(B(\theta, \theta^{(i)})\) 是 \(L(\theta)\) 的一个下界，而且由上式可知，

\[L(\theta^{(i)}) = B(\theta^{(i)}, \theta^{(i)}) \]

因此，任何可以使 \(B(\theta, \theta^{(i)})\) 增大的 \(\theta\)，也可以使 \(L(\theta)\) 增大。为了使 \(L(\theta)\) 有尽可能大的增长，选择 \(\theta^{(i+1)}\) 使 \(B(\theta, \theta^{(i)})\) 达到极大，即

\[\theta^{(i+1)} = \arg \max \limits_{\theta} B(\theta, \theta^{(i)}) \]

假设当前对于 \(L(\theta)\) 中参数 \(\theta\) 的取值为 \(\theta^{(i)}\)，求得 \(\theta^{(i+1)}\) 后，有

\[L(\theta^{(i+1)}) \ge B(\theta^{(i+1)}, \theta^{(i)}) \ge B(\theta^{(i)}, \theta^{(i)}) = L(\theta^{(i)}) \]

可见，\(L(\theta)\) 确实是在逐步增大。

现在求 \(\theta^{(i+1)}\) 的表达式，省去对 \(\theta\) 的极大化而言是常数的项，有

\[\begin{align} \theta^{(i+1)} & = \arg \max \limits_{\theta} \big( L(\theta^{(i)}) + \sum_Z P(Z|Y, \theta^{(i)}) \log \frac{P(Y|Z, \theta)P(Z|\theta)}{P(Z|Y, \theta^{(i)}) P(Y|\theta^{(i)})} \big) \notag \\ & = \arg \max \limits_{\theta} \big( \sum_Z P(Z|Y, \theta^{(i)}) \log( P(Y|Z, \theta)P(Z|\theta ) \big) \notag \\ & = \arg \max \limits_{\theta} \big( \sum_Z P(Z|Y, \theta^{(i)}) \log P(Y, Z|\theta) \big) \tag{$Q$ 函数}\\ & = \arg \max \limits_{\theta} Q(\theta, \theta^{(i)}) \notag \end{align} \]

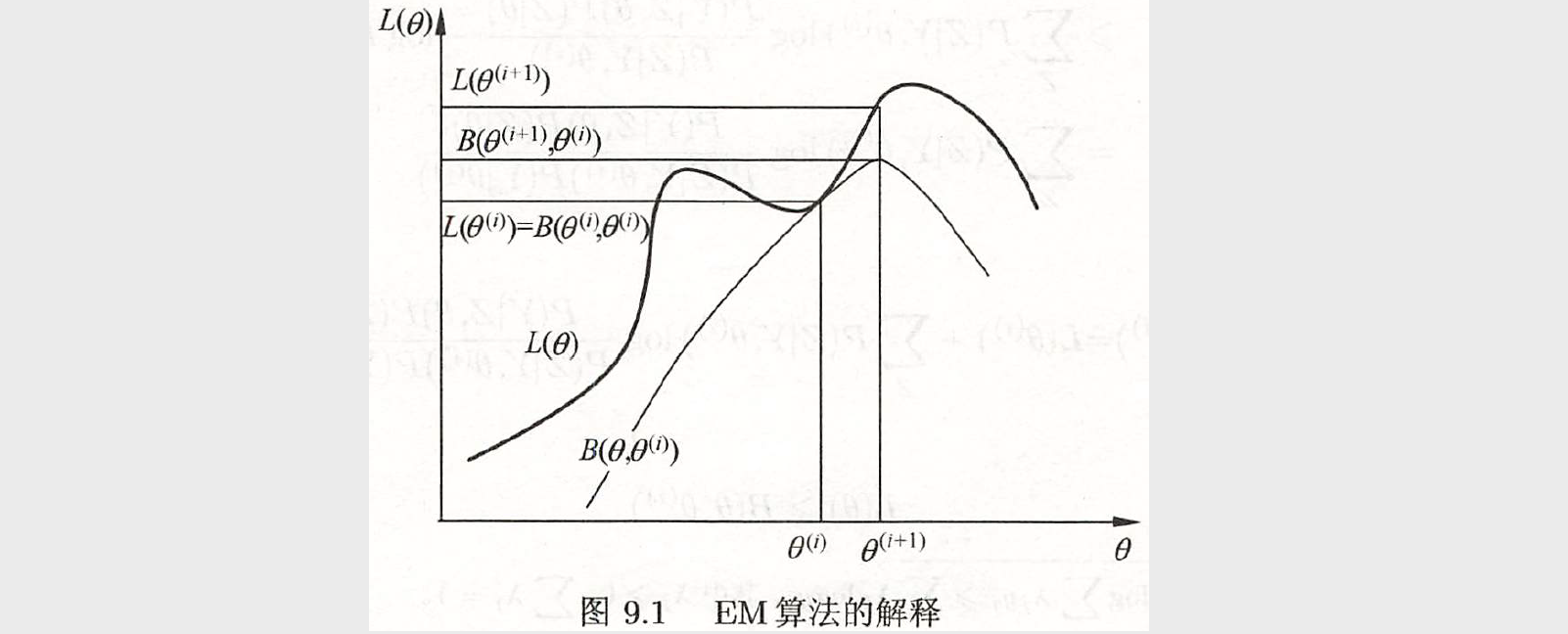
下图给出 EM 算法的直观解释，\(B(\theta, \theta^{(i)})\) 为对数似然函数 \(L(\theta)\) 的下界。两个函数在点 \(\theta = \theta^{(i)}\) 处相等。由上面的式子，EM 算法找到下一个点 \(\theta^{(i+1)}\) 使函数 \(B(\theta, \theta^{(i)})\) 极大化，也是函数 \(Q(\theta, \theta^{(i)})\) 极大化。这时由于 \(L(\theta) \ge B(\theta, \theta^{(i)})\)，函数 \(B(\theta, \theta^{(i)})\) 的增加，保证对数似然函数 \(L(\theta)\) 在每次迭代中也是增加的。EM 算法在点 \(\theta^{(i+1)}\) 重新计算 \(Q\) 函数值，进行下一次迭代。在这个过程中，对数似然函数 \(L(\theta)\) 不断增大。从图可以推断出 EM 算法不能保证找到全局最优值。

2 高斯混合模型（Gaussian mixture model, GMM）

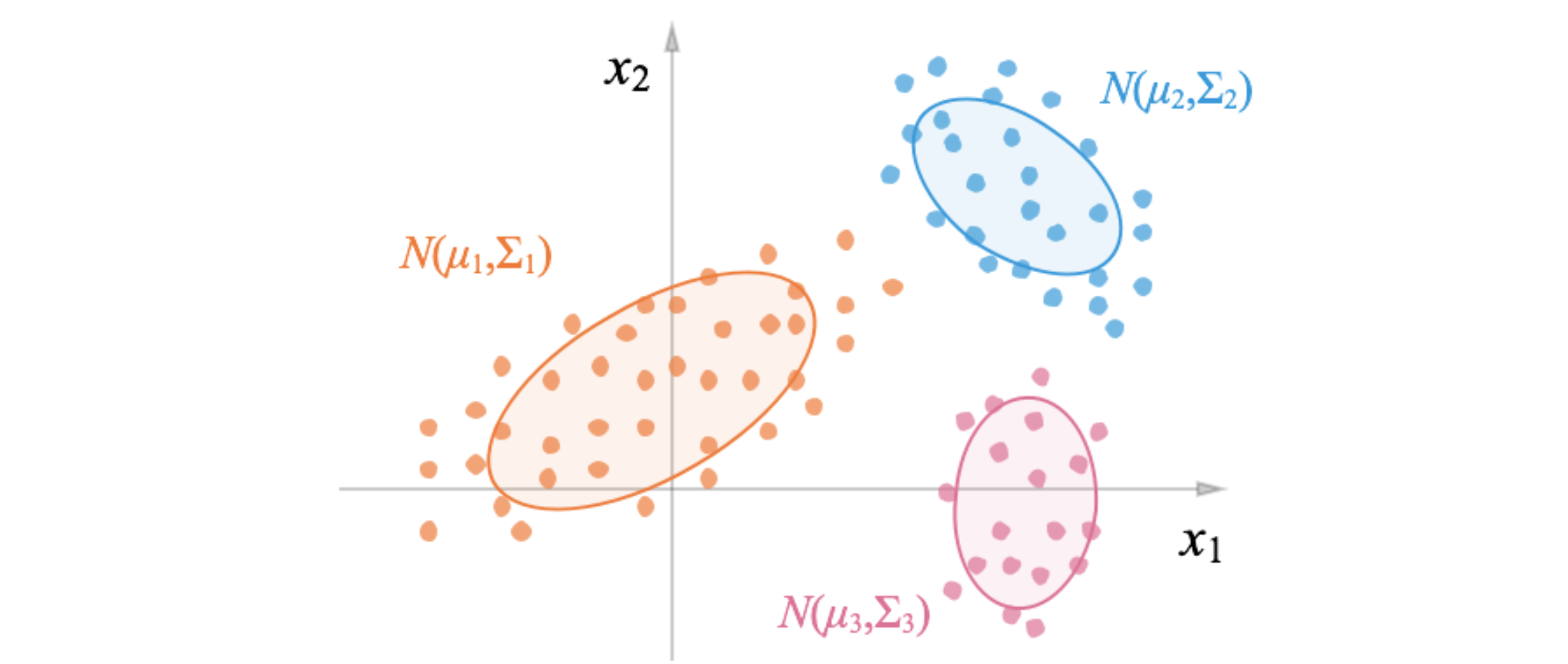
高斯混合模型是一种常见的聚类算法，EM 算法的一个重要应用是高斯混合模型的参数估计。

2.1 高斯混合模型定义

定义（高斯混合模型） \(\quad\) 高斯混合模型是指具有如下形式的概率分布模型：

\[P(y|\theta) = \sum_{k=1}^{K} \alpha_k \phi(y|\theta_k) \]

其中，\(\alpha_k \ge 0\)，\(\sum_{k=1}^{K} \alpha_k = 1\)；\(\phi(y|\theta_k)\) 是高斯分布密度，\(\theta_k = (\mu_k, \sigma_k^2)\)，

\[\phi(y|\theta_k) = \frac{1}{\sqrt{2\pi}\sigma_k} \exp \big[ - \frac{(y - \mu_k)^2}{2 \sigma_k^2} \big] \]

称为第 \(k\) 个分模型。

一般混合模型可以由任意概率分布密度函数代替高斯分布密度函数。

2.2 高斯混合模型参数估计的 EM 算法

假设观测数据 \(y_1, y_2, \cdots, y_N\) 由高斯混合模型生成，

\[P(y|\theta) = \sum_{k=1}^{K} \alpha_k \phi(y|\theta_k) \]

其中，\(\theta = (\alpha_1, \alpha_2, \cdots, \alpha_K; \theta_1, \theta_2, \cdots, \theta_K)\)。下面我们用 EM 算法估计高斯混合模型的参数 \(\theta\)。

1. 明确隐变量，写出完全数据的对数似然函数

可以设想观测数据 \(y_j, j=1, 2, \cdots, N,\) 是这样产生的：（1）首先依概率 \(\alpha_k\) 随机选择第 \(k\) 个高斯分布模型 \(\phi(y|\theta_k)\)，（2）然后依第 \(k\) 个分模型的概率分布 \(\phi(y|\theta_k)\) 生成观测数据 \(y_j\)。

这时观测数据 \(y_j, j=1, 2, \cdots, N\) 是已知的；反映观测数据 \(y_j\) 来自第 \(k\) 个分模型的数据是未知的，\(k=1, 2, \cdots, K\)，以隐变量 \(\gamma_{jk}\) 表示，其定义如下：

\[\begin{equation} \gamma_{jk} = \left\{ \begin{aligned} 1, \quad & 第 j 个观测来自第 k 个分模型 \\ 0, \quad & 否则 \end{aligned} \right. \end{equation} \]

\(j=1, 2, \cdots, N; \ k = 1, 2, \cdots, K\)，\(\gamma_{jk}\) 是 0-1 随机变量。

有了观测数据 \(y_j\) 及未观测数据 \(\gamma_{jk}\)，那么完整数据是

\[(y_j, \gamma_{j1}, \gamma_{j2}, \cdots, \gamma_{jK}) \quad j=1, 2, \cdots, N \]

于是可以写出完全数据的似然函数，一组完全数据 \((y_j, \gamma_{j1}, \gamma_{j2}, \cdots, \gamma_{jK})\) 的似然函数为

\[P(y_j, \gamma_{j1}, \gamma_{j2}, \cdots, \gamma_{jK} | \theta) = \prod_{k=1}^{K} \big[\alpha_k \phi(y_j | \theta_k) \big]^{\gamma_{jk}} \]

整个完全数据集 \((y, \gamma)\) 的似然函数为

\[\begin{aligned} P(y,\gamma|\theta) &= \prod_{j=1}^{N} P(y_j, \gamma_{j1}, \gamma_{j2}, \cdots, \gamma_{jK} | \theta) \\ &= \prod_{j=1}^{N} \prod_{k=1}^{K} \big[\alpha_k \phi(y_j|\theta_k) \big]^{r_{jk}} \\ &= \prod_{j=1}^{N} \prod_{k=1}^{K} \alpha_k^{\gamma_{jk}} \big[\frac{1}{\sqrt{2\pi}\sigma_k} \exp \big( - \frac{(y_j - \mu_k)^2}{2 \sigma_k^2} \big) \big]^{\gamma_{jk}} \end{aligned} \]

那么完全数据的对数似然函数为

\[\log P(y, \gamma | \theta) = \sum_{k=1}^{K} \sum_{j=1}^{N} \gamma_{jk} \Big\{ \log \alpha_k + \big[ \log \big( \frac{1}{\sqrt{2\pi}}\big) - \log \sigma_k - \frac{1}{2 \sigma_k^2}(y_j - \mu_k)^2 \big] \Big\} \]

2. EM 算法的 E 步：确定 \(Q\) 函数

\[\begin{aligned} Q(\theta, \theta^{(i)}) &= E_{\gamma}[\log P(y, \gamma | \theta) | y, \theta^{(i)}] \\ &= E_{\gamma}\Big\{\sum_{k=1}^{K} \sum_{j=1}^{N} \gamma_{jk} \Big\{ \log \alpha_k + \big[ \log \big( \frac{1}{\sqrt{2\pi}}\big) - \log \sigma_k - \frac{1}{2 \sigma_k^2}(y_j - \mu_k)^2 \big] \Big\} \Big\} \\ &= \sum_{k=1}^{K} \sum_{j=1}^{N} E(\gamma_{jk}) \Big\{ \log \alpha_k + \big[ \log \big( \frac{1}{\sqrt{2\pi}}\big) - \log \sigma_k - \frac{1}{2 \sigma_k^2}(y_j - \mu_k)^2 \big] \Big\} \end{aligned} \]

定义（响应度） \(\quad\) 计算 \(E(\gamma_{jk} | y, \theta)\)，记为 \(\hat{\gamma}_{jk}\)

\[\begin{aligned} \hat{\gamma}_{jk} &= E(\gamma_{jk} | y, \theta) = 0 \times P(\gamma_{jk} = 0 | y, \theta) + 1 \times P(\gamma_{jk} = 1 | y, \theta) \\ &= \frac{P(\gamma_{jk} = 1, y| \theta)}{P(y| \theta)} \\ &= \frac{P(\gamma_{jk} = 1, y_j| \theta)}{\sum \limits_{k=1}^{K} P(\gamma_{jk} = 1, y_j| \theta)} \\ &= \frac{P(y_j| \gamma_{jk} = 1, \theta) P(\gamma_{jk} = 1 | \theta)}{\sum \limits_{k=1}^{K} P(y_j| \gamma_{jk} = 1, \theta) P(\gamma_{jk} = 1 | \theta)} \\ &= \frac{\alpha_k \phi(y_j | \theta_k)}{\sum \limits_{k=1}^{K}\alpha_k \phi(y_j | \theta_k)}, \quad j=1, 2, \cdots, N; \quad k=1, 2, \cdots, K \end{aligned} \]

\(\hat{\gamma}_{jk}\) 是在当前模型参数下第 \(j\) 个观测数据来自第 \(k\) 个分模型的概率，称为分模型 \(k\) 对观测数据 \(y_j\) 的响应度。

将 \(\hat{\gamma}_{jk}\) 带入上面 \(Q(\theta, \theta^{(i)})\)，即得

\[Q(\theta, \theta^{(i)}) = \sum_{k=1}^{K} \sum_{j=1}^{N} \hat{\gamma}_{jk} \Big\{ \log \alpha_k + \big[ \log \big( \frac{1}{\sqrt{2\pi}}\big) - \log \sigma_k - \frac{1}{2 \sigma_k^2}(y_j - \mu_k)^2 \big] \Big\} \]

3. 确定 EM 算法的 M 步

迭代的 M 步是求函数 \(Q(\theta, \theta^{(i)})\) 对 \(\theta\) 的极大值，即求新一轮迭代的模型参数：

\[\theta^{(i+1)} = \arg \max \limits_{\theta} Q(\theta, \theta^{(i)}) \]

用 \(\hat{\mu}_k, \hat{\sigma}_k\) 及 \(\hat{\alpha}_k, k = 1, 2, \cdots, K\)，表示 \(\theta^{(i+1)}\) 的各参数，在求解过程中，同时需要满足 \(\sum_{k=1}^{K} \alpha_k = 1\)，于是有：

\[\begin{aligned} & \arg \max \limits_{\theta} Q(\theta, \theta^{(i)}) \\ s.t. \quad & \sum_{k=1}^{K} \alpha_k = 1 \end{aligned} \]

采用拉格朗日乘子法，有

\[L(\theta) = Q(\theta, \theta^{(i)}) + \lambda (\sum_{k=1}^{K}\alpha_k - 1) \]

对 \(\mu_k, \sigma_k^2\) 和 \(\alpha_k\) 求偏导数并令其为 0，得

\[\begin{aligned} & \hat{\mu}_k = \frac{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk} y_j}{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk}} \\ & \hat{\sigma}_k^2 = \frac{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk} (y_j - \mu_k)^2}{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk}} \\ & \hat{\alpha}_k = \frac{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk}}{N}, \quad k = 1, 2, \cdots, K \\ \end{aligned} \]

参数 \(\hat{\alpha}_k\) 的详细推导：

\[\frac{\partial{L(\theta)}}{\partial{\alpha_k}} = \frac{\sum_{j=1}^{N} \hat{\gamma}_{jk}}{\alpha_k} + \lambda = 0 \]

于是有

\[\sum_{j=1}^{N} \hat{\gamma}_{jk} + \lambda \alpha_k = 0 \]

等式两边同时对 \(k\) 求和

\[\sum_{k=1}^{K}\sum \limits_{j=1}^{N} \hat{\gamma}_{jk} + \lambda \sum_{k=1}^{K}\alpha_k = 0 \]

得

\[N + \lambda = 0 \]

因此有

\[\hat{\alpha}_k = \frac{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk}}{N} \]

重复以上计算，知道对数似然函数值不再有明显的变化为止。

算法（高斯混合模型参数估计的 EM 算法）

输入： 观测数据 \(y_1, y_2, \cdots, y_N\)，高斯混合模型；
输出：高斯混合模型参数。
（1）取参数的初始值开始迭代；
（2）E 步：依据当前模型参数，计算分模型 \(k\) 对观测数据 \(y_j\) 的响应度

\[\hat{\gamma}_{jk} = \frac{\alpha_k \phi(y_j | \theta_k)}{\sum \limits_{k=1}^{K}\alpha_k \phi(y_j | \theta_k)}, \quad j=1, 2, \cdots, N; \quad k=1, 2, \cdots, K \]

（3）M 步：计算新一轮迭代的模型参数

\[\begin{aligned} & \hat{\mu}_k = \frac{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk} y_j}{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk}} \\ & \hat{\sigma}_k^2 = \frac{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk} (y_j - \mu_k)^2}{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk}} \\ & \hat{\alpha}_k = \frac{\sum \limits_{j=1}^{N} \hat{\gamma}_{jk}}{N}, \quad k = 1, 2, \cdots, K \\ \end{aligned} \]

（4）重复第（2）步和第（3）步，知道收敛。

3 高斯混合模型的应用

3.1 AIC 和 BIC

待补充

3.2 高斯混合模型用于聚类

# 导入模块
import numpy as np
from sklearn.datasets import make_blobs  
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt

# 生成数据
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)

确定簇的数量：

n_components = np.arange(1, 21)
models = [GaussianMixture(n, covariance_type='full', random_state=0).fit(X) for n in n_components]
# plt.figure(figsize=(8, 6)) 
plt.plot(n_components, [m.bic(X) for m in models], label='BIC')
plt.plot(n_components, [m.aic(X) for m in models], label='AIC')
plt.legend(loc='best')
plt.xticks(range(0, 22))
plt.xlabel('n_components')

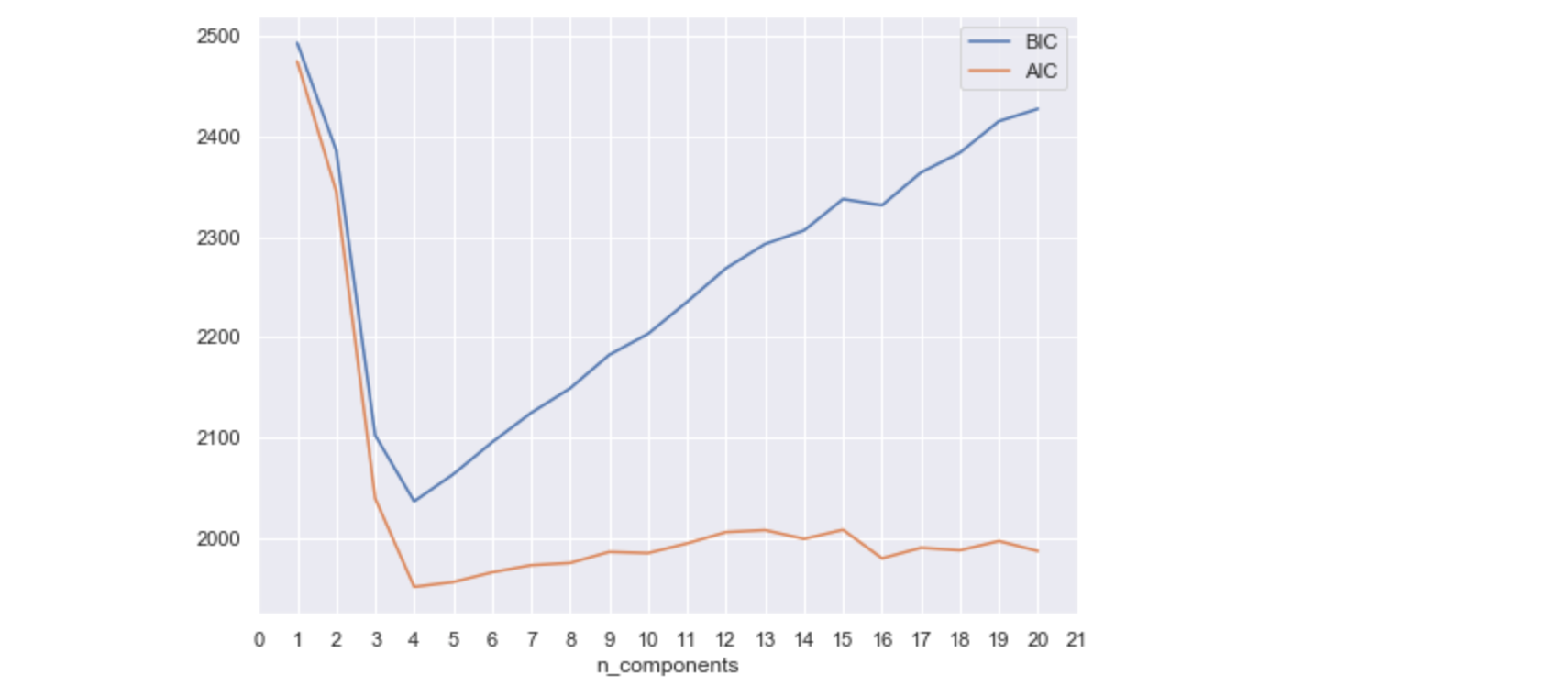
我们使用最佳聚类数（在这种情况下为4）训练模型，并将聚类结果和原始数据进行对比：

gmm = GaussianMixture(n_components=4, init_params='kmeans')  # 参数初始化方法
gmm.fit(X)
y_pred = gmm.predict(X)

figure, axes = plt.subplots(1, 2, figsize=(10, 4), dpi=100)
axes[0].scatter(X[:,0], X[:,1], c=y, cmap='rainbow')
axes[0].set_title("original clusters")
axes[1].scatter(X[:,0], X[:,1], c=y_pred, cmap='rainbow')
axes[1].set_title("GMM clusters")
plt.show()

3.3 高斯混合模型和 K-Means 的异同

高斯混合模型与 K-Means 算法的相同点是：

（1）它们都是可用于聚类的算法；
（2）都需要指定 K 值；
（3）都是使用 EM 算法来求解；
（4）都往往只能收敛于局部最优。

而它相比于 K 均值算法的优点是：

（1）可以给出一个样本属于某类的概率是多少；
（2）不仅仅可以用于聚类，还可以用于概率密度的估计；
（3）并且可以用于生成新的样本点。

参考

1. 《统计学习方法》 李航
2. 高斯混合模型(Gaussian Mixture Model)与EM算法原理
3. 如何通俗的理解高斯混合模型（Gaussian Mixture Models）
4. 《百面机器学习》