MCMC-蒙特卡罗法

蒙特卡罗法（Monte Carlo method），也称为统计模拟方法（statistical simulation method），是通过从概率模型的随机抽样进行近似数值计算的方法。蒙特卡罗来自于一个著名赌场的名字。

马尔科夫链蒙特卡罗法（Markov Chain Monte Carlo, MCMC），则是以马尔科夫链为概率模型的蒙特卡罗法。马尔科夫链蒙特卡罗法构建一个马尔科夫链，使其平稳分布就是要进行抽样的分布，首先基于该马尔科夫链进行随机游走，产生样本的序列，之后使用该平稳分布的样本进行近似数值计算。

Metropolis-Hastings 算法是最基本的马尔科夫链蒙特卡罗法，吉布斯抽样（Gibbs sampling）是最简单、使用最广泛的马尔科夫链蒙特卡罗法。

马尔科夫链蒙特卡罗法被应用于概率分布的估计、定积分的近似计算、最优化问题的近似求解等问题，特别是被应用于统计学习中概率模型的学习与推理，马尔科夫链蒙特卡罗法是重要的统计学习计算方法。

本节介绍一般的蒙特卡罗法在随机抽样、数学期望估计、定积分计算的应用。马尔科夫链蒙特卡罗法是蒙特卡罗法的一种方法。

1 随机抽样

统计学和机器学习的目的是基于数据对概率分布的特征进行推断，蒙特卡罗法要解决的问题是，假设概率分布的定义已知，通过抽样获得概率分布的随机样本，并通过得到的随机样本对概率分布的特征进行分析。比如，从样本得到经验分布，从而估计总体分布；或者从样本计算出样本均值，从而估计总体期望。所以蒙特卡罗法的核心是随机抽样（random sampling）。

一般的蒙特卡罗法有直接抽样法、接受-拒绝抽样法、重要性抽样法等。接受-拒绝抽样法、重要性抽样法适合于概率密度函数复杂（如密度函数含有多个变量，各变量互相不独立，密度函数形式复杂）不能直接抽样的情况。

一般而言，均匀分布 $Uniform(0, 1)$ 的样本是相对容易生成的，而我们常见的概率分布，无论连续的还是离散的分布，都可以基于 $Uniform(0, 1)$ 的样本生成。例如正态分布可以通过著名的 Box-Muller 变换得到。

Box-Muller 变换
如果随机变量 $U_1, U_2$ 独立，且 $U_1, U_2 \sim Uniform(0, 1)$，

\[Z_1 = \sqrt{-2\ln U_1} \cos(2\pi U_2) \]
\[Z_2 = \sqrt{-2\ln U_1} \sin(2\pi U_2) \]
则 $Z_1, Z_2$ 独立且服从标准正态分布。

其它几个著名的连续分布，包括指数分布、Gamma 分布、t 分布、F 分布、Beta 分布、Dirichlet 分布等等，也都可以通过类似的变换得到；离散的分布通过均匀分布更加容易生成。但是，我们并不总是幸运的，当 $p(x)$ 形式很复杂，或者 $p(x)$ 是高纬度的时候，样本的生成就比较困难了。

1.1 接受-拒绝抽样法（accept-reject sampling method）

假设有随机变量 $x$，取值 $x \in \mathcal{X}$，其概率密度函数为 $p(x)$，目标是得到该概率分布的随机样本，以对这个概率分布进行分析。

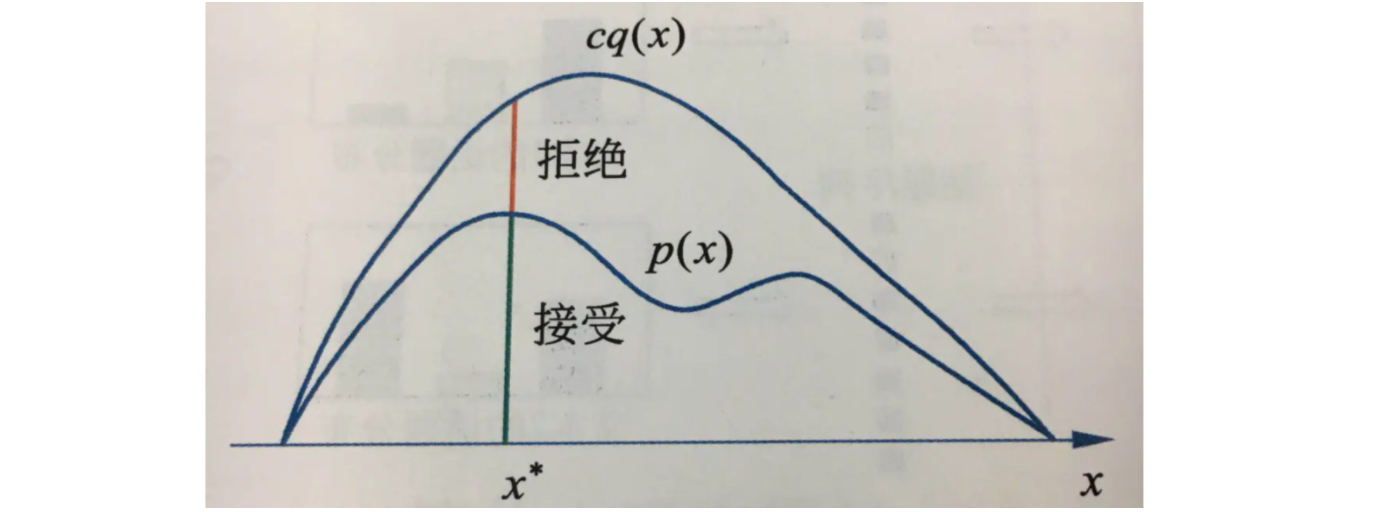
接受-拒绝法的基本想法如下。假设 $p(x)$ 不可以直接抽样。找一个可以直接抽样的分布，称为建议分布（proposal distribution）。假设 $q(x)$ 是建议分布的概率密度函数，并且有 $q(x)$ 的 $c$ 倍一定大于等于 $p(x)$，其中 $c \gt 0$（如图所示）。按照 $q(x)$ 进行抽样，假设得到结果是 $x^*$，再按照 $\frac{p(x^*)}{cq(x^*)}$ 的比例随机决定是否接受 $x^*$。直观上，落到 $p(x^*)$ 范围内的救接受（绿色），落到 $p(x^*)$ 范围外的就拒绝（红色）。接受-拒绝法实际是按照 $p(x)$ 的涵盖面积（或涵盖体积）占 $cq(x)$ 的涵盖面积（或涵盖体积）的比例进行抽样。

算法（接受-拒绝法）
输入：抽样的目标概率分布的概率密度函数 $p(x)$；
输出：概率分布的随机样本 $x_1, x_2, \cdots, x_n$。
参数：样本 $n$
（1）选择概率密度函数为 $q(x)$ 的概率分布作为建议分布，使其对任一 $x$ 满足 $cq(x) \geq p(x)$，其中 $c \gt 0$；
（2）按照建议分布 $q(x)$ 随机抽样得到样本 $x^*$，再按照均匀分布在 $(0, 1)$ 范围内抽样得到 $u$；
（3）如果 $u \leq \frac{p(x^*)}{cq(x^*)}$，则将 $x^*$ 作为抽样结果；否则，回到步骤（2）；
（4）直到得到 $n$ 个随机样本，结束。

1.2 接受-拒绝抽样法举例

假设我们要采样的分布为

\[p(x) = 0.3e^{-(z-0.3)^2} + 0.7e^{\frac{-(z-2)^2}{0.3}} \]

这是一个稍微复杂的分布，因此我们参考高斯分布 $q(x) \sim N(1.4, 1.2)$（其中均值和方差是经过计算和尝试得到的），以满足 $cq(x) \geq p(x)$，如图所示

import numpy as np
import matplotlib.pyplot as plt

def f1(x):
    return 0.3*np.exp(-(x-0.3)**2) + 0.7* np.exp(-(x-2.)**2/0.3)
def f2(x):
    sigma =1.2
    return 2.5/(np.sqrt(2*np.pi)*sigma)*np.exp(-0.5*(x-1.4)**2/sigma**2)
x = np.arange(-4., 6., 0.01)

plt.rcParams['figure.figsize'] = (6, 4)
plt.plot(x, f1(x), color = "red")
plt.plot(x, f2(x), color = "blue")
plt.xticks([])
plt.yticks([])
plt.ylim(0, 0.9)
plt.xlim(-4, 6)
plt.plot([0.3, 0.3], [0, 0.54601532], color="black")
plt.plot(0.3, 0.54601532, 'b.')
plt.fill_between(x, f1(x), f2(x), color=(0.7, 0.7, 0.7))
plt.annotate('$x^*$', xy=(0.,0), xytext=(0.2, -0.08), fontsize=15)
plt.annotate('$u$', xy=(0.,0.), xytext=(0.35, 0.15), fontsize=15)
plt.annotate('$cq(x^*)$', xy=(0., 0.), xytext=(-0.4, 0.55), fontsize=15)
plt.annotate('$p(x)$', xy=(0., 0.), xytext=(2.0, 0.15), fontsize=15)
plt.annotate('$cq(x)$', xy=(0., 0.), xytext=(1.3, 0.85), fontsize=15)
for spine in plt.gca().spines.keys():
    if spine == "top" or spine == "right" or spine == "left":
        plt.gca().spines[spine].set_color("none")
plt.show()

使用接受-拒绝抽样法来进行样本抽样，并将样本分布图可视化

import numpy as np
import matplotlib.pyplot as plt

def f1(x):
    return (0.3*np.exp(-(x-0.3)**2) + 0.7* np.exp(-(x-2.)**2/0.3))/1.2113
x = np.arange(-4., 6., 0.01)
plt.plot(x, f1(x), color="red")

size = int(1e+07)
sigma = 1.2
z = np.random.normal(loc=1.4, scale=sigma, size=size)
qz = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-0.5*(z-1.4)**2/sigma**2)
c = 2.5
#z = np.random.uniform(low=-4, high=6, size=size)
#qz = 0.1
#c = 10
u = np.random.uniform(low=0, high=c*qz, size=size)

pz =  0.3*np.exp(-(z-0.3)**2) + 0.7* np.exp(-(z-2.)**2/0.3)
sample = z[pz >= u]
plt.rcParams['figure.figsize'] = (8, 4)
plt.yticks([])
plt.hist(sample, bins=150, normed=True, edgecolor='black')
for spine in plt.gca().spines.keys():
    if spine == "top" or spine == "right" or spine == "left":
        plt.gca().spines[spine].set_color("none")
plt.show()

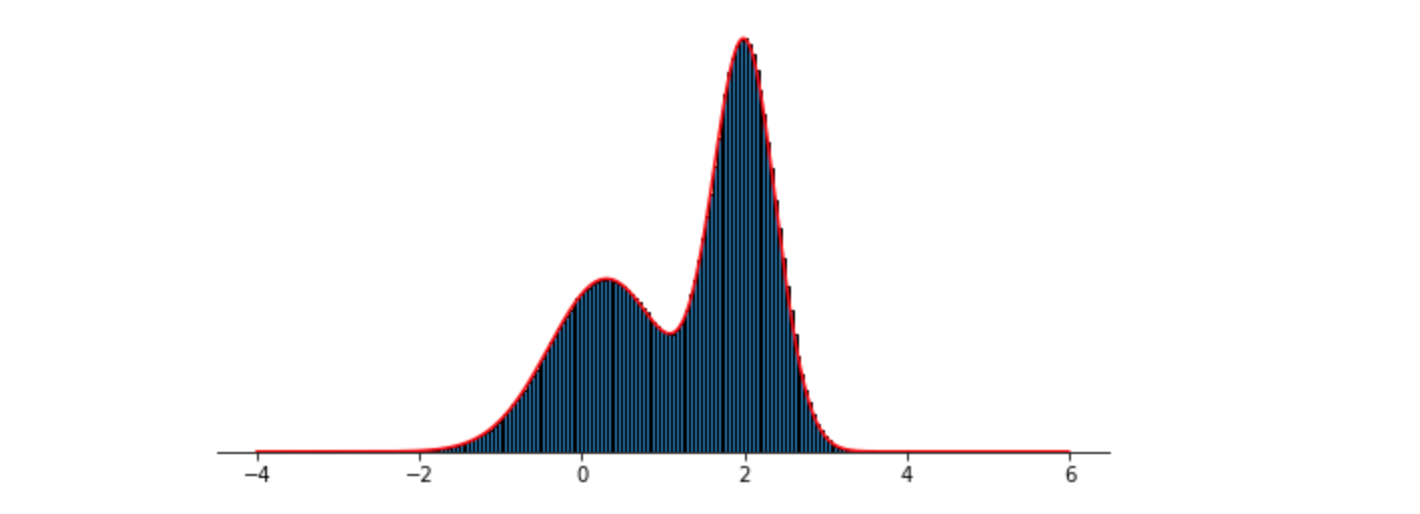
可以看到，采样结果完全符合原分布。另外把参考分布换为均匀分布(代码中z, q, k换为注释部分)，仍然得到较好的采样结果，如下图

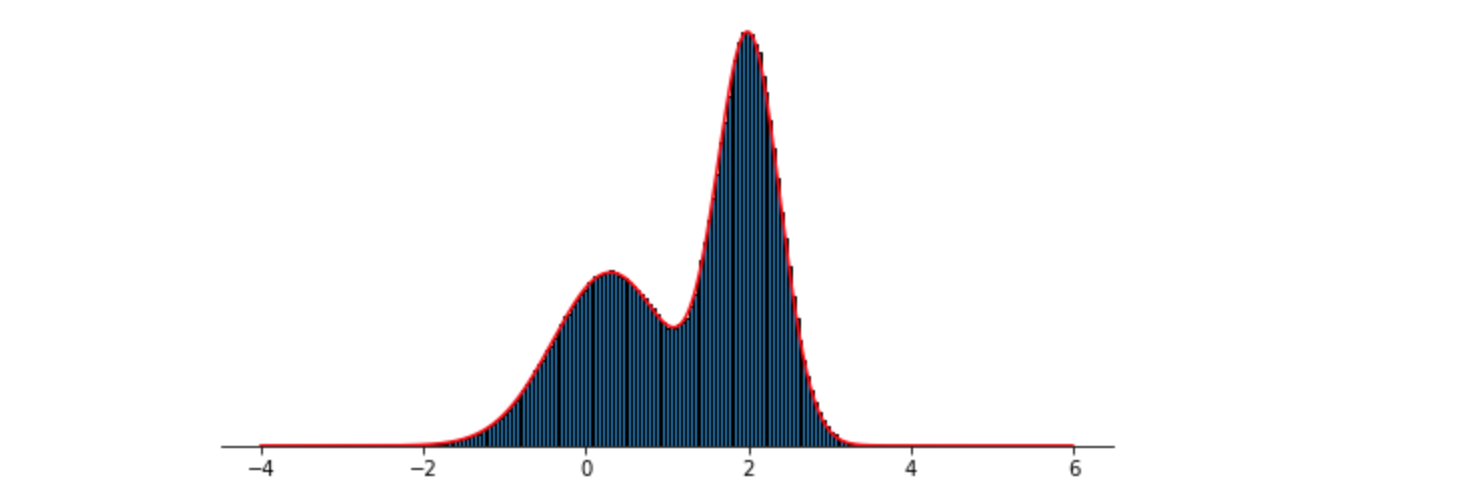
接受-拒绝法的优点是容易实现，缺点是效率可能不高。如果 $p(x)$ 的涵盖体积占 $cq(x)$ 的涵盖体积的比例很低，就会导致拒绝的比例很高，抽样效率很低。注意，一般是在高维空间上抽样，即使 $p(x)$ 与 $cq(x)$ 很接近，两者涵盖体积的差异也可能很大（与我们在三维空间的直觉不同）。

2 数学期望估计

一般的蒙特卡罗法，如直接抽样法、接受-拒绝抽样法、重要性抽样法，也可以用于数学期望估计（estimation of mathematical expectation）。假设有随机变量 $x$，取值 $x \in \mathcal{X}$，其概率密度函数为 $p(x)$，$f(x)$ 为定义在 $\mathcal{X}$ 上的函数，目标是求函数 $f(x)$ 关于密度函数 $p(x)$ 的数学期望 $E_{p(x)}[f(x)]$。

针对这个问题，蒙特卡罗法按照概率分布 $p(x)$ 独立地抽取 $n$ 个样本 $x_1, x_2, \cdots, x_n,$ 比如用以上的三种抽样方法，之后计算函数 $f(x)$ 的样本均值 $\hat{f}_n$

\[\hat{f}_n = \frac{1}{n}\sum_{i=1}^{n}f(x_i) \]

作为数学期望 $E_{p(x)}[f(x)]$ 的近似值。

根据大数定律可知，当样本容量增大时，样本均值以概率 1 收敛于数学期望：

\[\hat{f}_n \rightarrow E_{p(x)}[f(x)], \quad n \rightarrow \infty \]

这样就得到了数学期望的近似计算方法：

\[E_{p(x)}[f(x)] \approx \frac{1}{n}\sum_{i=1}^{n}f(x_i) \]

3 积分计算

一般的蒙特卡罗法也可以用于定积分的近似计算，称为蒙特卡罗积分（Monte Carlo integration）。假设有一个函数 $h(x)$，目标是计算该函数在 $[a, b]$ 上的积分

\[\int_{a}^{b}h(x)dx \]

如图

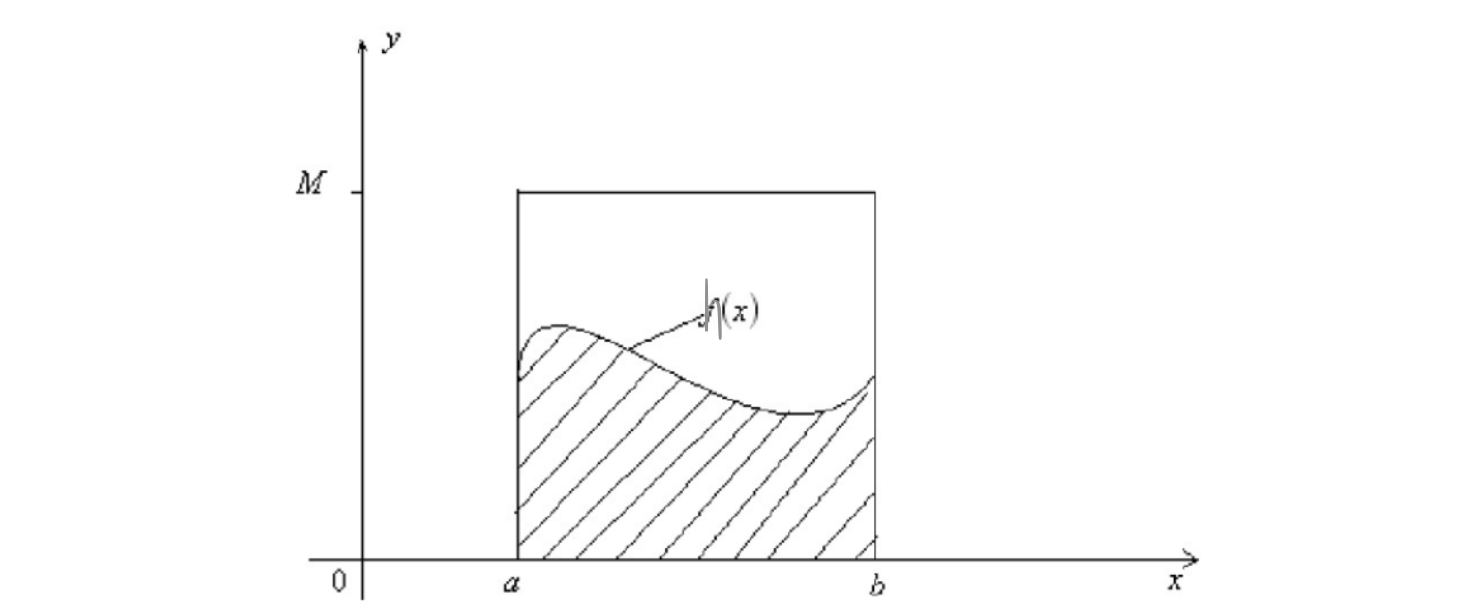
如果我们很难求出 $h(x)$ 的原函数，那么这个积分就比较难求解。那么我们可以使用近似求解的方法。

一个简单的近似求解的方法是在 $[a, b]$ 之间随机的采样一个点。比如 $x_0$，然后用 $h(x_0)$ 代替在 $[a, b]$ 区间上所有的 $h(x)$ 的值。那么上面的定积分的近似求解为：
\[(b - a) h(x_0) \]
当然，用一个值代表 $[a, b]$ 区间上的所有 $h(x)$ 的值，这个假设太粗糙。那么我们可以在 $[a, b]$ 上采样 $n$ 个值 $x_0, x_1, \cdots, x_{n-1}$，用它们的值来代表 $[a, b]$ 区间上的所有 $h(x)$ 的值。这样上面的积分近似求解为：
\[\frac{b - a}{n}\sum_{i=0}^{n-1}h(x_i) \]
虽然上面的方法可以在一定程度上求解出近似的解，但是它隐含了一个假设，即 $x$ 在 $[a, b]$ 之间是服从均匀分布的，而绝大部分情况是，$x$ 并不服从均匀分布。如果假设不成立，则模拟求出的结果很可能和真实值相差甚远。
那么如何解决这个问题呢？我们可以将蒙特卡罗法应用于定积分。如果能够将函数 $h(x)$ 分解成一个函数 $f(x)$ 和一个概率密度函数 $p(x)$ 的乘积的形式，那么就有
\[\int_{a}^{b}h(x)dx = \int_{a}^{b} f(x)p(x)dx = E_{p(x)}[f(x)] \]
于是函数 $h(x)$ 的积分可以表示为函数 $f(x)$ 关于概率密度函数 $p(x)$ 的数学期望。实际上，给定一个概率密度函数 $p(x)$，只要取 $f(x) = \frac{h(x)}{p(x)}$，就可以得到上式。就是说，任何一个函数的积分都可以表示为某一个函数的数学期望的形式。而函数的数学期望又可以通过函数的样本均值估计。于是，就可以利用样本均值来近似计算积分。这就是蒙特卡罗积分的基本想法。

\[\int_{a}^{b}h(x)dx = E_{p(x)}[f(x)] \approx \frac{1}{n}\sum_{i=1}^{n}f(x_i) \]

例用蒙特卡罗积分法求 $\int_{-\infty}^{\infty}x \frac{1}{\sqrt{2\pi}}\exp\big(\frac{-x^2}{2} \big)dx$。
解令 $f(x) = x$

\[p(x) = \frac{1}{\sqrt{2\pi}}\exp\big(\frac{-x^2}{2} \big) \]
$p(x)$ 是标准正态分布的密度函数。使用蒙特卡罗积分法，按照标准正态分布在区间 $(-\infty, \infty)$ 抽样 $x_1, x_2, \cdots, x_n$，取其平均值，就得到要求的积分值。当样本增大时，积分趋于 0。

马尔科夫链蒙特卡罗法也适合于概率密度函数复杂，不能直接抽样的情况，旨在解决一般的蒙特卡罗法，如接受-拒绝抽样法、重要性抽样法，抽样效率不高的问题。一般的蒙特卡罗法中的抽样样本是独立的，而马尔科夫链蒙特卡罗法中的抽样样本不是独立的，样本序列形成马尔科夫链。

4 小结

使用接受-拒绝抽样法，我们可以解决一些概率分布不是常见的分布的情况，得到其采样集并用蒙特卡罗法求和的目的。但是接受-拒绝抽样法也只能部分满足我们的需求，在很多时候我们还是很难得到我们的概率分布的样本集。比如：

对于一些二维分布 $p(x, y)$，有时候我们只能得到条件分布 $p(x|y)$ 和 $p(y|x)$，却很难得到二维分布 $p(x, y)$ 的一般形式，这时我们无法用接受-拒绝抽样法得到其样本集。
对于一些高维的复杂非常见分布 $p(x_1, x_2, \cdots, x_n)$，我们要找到一个合适的 $q(x)$ 和 $c$ 非常困难。

从上面可以看出，要想将蒙特卡罗法作为一个通用的采样模拟求和的方法，必须解决如何方便得到各种复杂概率分布的对应的采样样本集的问题。而马尔科夫链就是帮助找到这些复杂概率分布的对应的采样样本集的方法。

参考

posted @ 2021-04-01 13:52 Hiidiot 阅读(662) 评论(0) 编辑收藏举报

刷新页面返回顶部