hdu_3483A Very Simple Problem(C(m,n)+快速幂矩阵)

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3483

A Very Simple Problem

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 945    Accepted Submission(s): 471

Problem Description

This is a very simple problem. Given three integers N, x, and M, your task is to calculate out the following value:

 

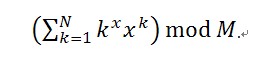
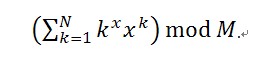
Input

There are several test cases. For each case, there is a line with three integers N, x, and M, where 1 ≤ N, M ≤ 2*10⁹, and 1 ≤ x ≤ 50.
The input ends up with three negative numbers, which should not be processed as a case.

 

Output

For each test case, print a line with an integer indicating the result.

 

Sample Input

100 1 10000 3 4 1000 -1 -1 -1

 

Sample Output

5050 444

 

Source

2010 ACM-ICPC Multi-University Training Contest（5）——Host by BJTU

 

//计算排列数（杨辉三角）
//C(m,n) = C(m-1,n-1)+C(m-1,n)
//快速幂
/*
*  [题意]
*   输入n, x, m
*   求(1^x)*(x^1)+(2^x)*(x^2)+(3^x)*(x^3)+...+(n^x)*(x^n)
*  [解题方法]
*   设f[n] = [x^n, n*(x^n), (n^2)*(x^n),..., (n^x)*(x^n)]
*   则f[n][k] = (n^k)*(x^n)
*   问题转化为求：( g[n] = f[1][x]+f[2][x]+...+f[n][x] )
*   设C(i,j)为组合数，即i种元素取j种的方法数
*   所以有：f[n+1][k] = ((n+1)^k)*(x^(n+1)) （二次多项式展开）
*                     = x*( C(k,0)*(x^n)  +C(k,1)*n*(x^n)+...+C(k,k)*(n^k)*(x^n) )
*                     = x*( C(k,0)*f[n][0]+C(k,1)*f[n][1]+...+C(k,k)*f[n][k] )
*   所以得：
*   |x*1 0................................0|        |f[n][0]|       |f[n+1][0]|
*   |x*1 x*1 0............................0|        |f[n][1]|       |f[n+1][1]|
*   |x*1 x*2 x*1 0........................0|    *   |f[n][2]|   =   |f[n+1][2]|
*   |......................................|        |.......|       |.........|
*   |x*1 x*C(k,1) x*C(k,2)...x*C(k,x) 0...0|        |f[n][k]|       |f[n+1][k]|
*   |......................................|        |.......|       |.........|
*   |x*1 x*C(x,1) x*C(x,2).......x*C(x,x) 0|        |f[n][x]|       |f[n+1][x]|
*   |0................................0 1 1|        |g[n-1] |       | g[ n ]  |
*/
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define ll long long
const ll maxn = 55;
ll c[maxn][maxn];
ll n, mod, x, m;
struct Mat{
    ll f[maxn][maxn];
};
void init()
{
    ll i,j,k;
    c[0][0] = c[1][0] = c[1][1] = 1;
    for(i = 2; i < maxn; i++){
        c[i][0] = c[i][i] = 1;
        for(j = 1; j < i; j++){
            c[i][j] = c[i-1][j]+c[i-1][j-1];
        }
    }
}
Mat operator *(Mat a, Mat b)
{
    ll i, j, k;
    Mat c;
    memset(c.f,0,sizeof(c.f));
    for(k = 0; k < m; k++){
        for(i = 0; i < m; i++){
            for(j = 0; j < m; j++){
                if(!b.f[k][j]) continue;
                c.f[i][j] = (c.f[i][j]+(a.f[i][k]*b.f[k][j])%mod)%mod;
            }
        }
    }
    return c;
}
Mat multi(Mat a,ll b)
{
    Mat s;
    memset(s.f,0,sizeof(s.f));
    for(int i = 0; i < m; i++){
        s.f[i][i] = 1;
    }
    while(b){
        if(b&1) s = s*a;
        a = a*a;
        b>>=1;
    }
    return s;
}
int main()
{
    init();
    while(~scanf("%lld%lld%lld",&n,&x,&mod))
    {
        if(n<0&&x<0&&mod<0) break;
        Mat e;
        ll i, j;
        ll ans = 0;
        memset(e.f,0,sizeof(e.f));
        for(i = 0; i <= x; i++){
            for(j = i; j <= x; j++){
                e.f[j][i] = c[x-i][j-i]*x%mod;
            }
        }
        e.f[0][x+1] = e.f[x+1][x+1] = 1;
        m = x+2;
        e = multi(e,n);
        for(i = 0; i < m-1; i++) ans = (ans+x*e.f[i][m-1])%mod;
        printf("%lld\n",(ans+mod)%mod);
    }
    return 0;
}