An Easy Problem?!（细节题，要把所有情况考虑到）

http://poj.org/problem?id=2826

An Easy Problem?!

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 10505		Accepted: 1584

Description

It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width. 

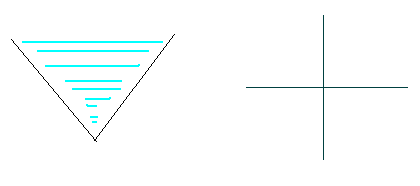
Your mission is to calculate how much rain these two boards can collect. 

Input

The first line contains the number of test cases. 
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x₁, y₁, x₂, y₂, x₃, y₃, x₄, y₄. (x₁, y₁), (x₂, y₂) are the endpoints of one board, and (x₃, y₃), (x₄, y₄) are the endpoints of the other one. 

Output

For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected. 

Sample Input

2
0 1 1 0
1 0 2 1

0 1 2 1
1 0 1 2

Sample Output

1.00
0.00

题解：判断可以接多少水，如果两直线可以接水的话，求三角形面积
下面给出一些计算几何最基础的结论（常用） 
两向量点乘： a*b*cosO = x1*y1+x2*y2 用来 1 ：计算夹角 2：计算投影
两向量叉乘： a*b*sinO = x1*y1-x2*y2 用来 1：计算面积  2:判断点在直线的哪边，右手法则
这个题输出的时候要注意，用G++交题的时候要最后输出ans+eps;
下面是代码：

#include <cmath>
#include <cstdio>
#include <algorithm> 
using namespace std;

#define N 105
#define eps 1e-6//精度太小会导致出错，精度太大会增加计算量，自己权衡 
struct point {
    double x, y;
    point(){}
    point(double x, double y):x(x), y(y){}
    point operator + (const point o) const{
        return point(x+o.x, y+o.y);
    }
    point operator - (const point o) const{
        return point(x-o.x, y-o.y);
    }

    double operator * (const point o) const{
        return x*o.y - o.x*y;
    }

    double operator ^ (const point o) const{//点乘
        return x*o.x + y*o.y;
    }

    point operator * (const double a) const{
        return point(a*x, a*y);
    }

    double len2()
    {
        return x*x + y*y;
    }
}a, b, s, t;

point Intersection(point a, point b, point c, point d)
{
    double t = ((d - a)*(c - a))/((b - a)*(d - c));
    return a + (b-a)*fabs(t);
}

int main()
{
    point a, b, c, d;
    int T;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%lf %lf %lf %lf", &a.x, &a.y, &b.x, &b.y);
        scanf("%lf %lf %lf %lf", &c.x, &c.y, &d.x, &d.y);
        
        if(fabs(a.y - b.y) < eps || fabs(c.y - d.y) < eps)//有水平线 
        {
            puts("0.00");
            continue;
        }
        
        if(a.y < b.y) swap(a, b);
        if(c.y < d.y) swap(c, d);
        
        if(fabs((b.y-a.y)*(d.x-c.x) - (d.y-c.y)*(b.x-a.x)) < eps) //两条线平行 
        {
            puts("0.00");
            continue;
        }
        
        if(((b-a)*(c-a))*((b-a)*(d-a)) > 0 || ((d-c)*(a-c))*((d-c)*(b-c)) > 0)//两条线段根本没有交点 
        {
            puts("0.00");
            continue;
        }
        point p = Intersection(a, b, c, d); 
        point up = point(0,10); 
        if(((a-p)*(up)) * ((c-p)*(up)) > 0)//能收集雨水的部分在竖直线的同一侧
        {
            if((a-p)*(c-p) > 0 && c.x- a.x>= -eps)
            {
                puts("0.00");
                continue;
            }
            if((a-p)*(c-p) < 0 && a.x- c.x>= -eps)
            {
                puts("0.00");
                continue;
            }
        }
        point t1, t2;
        t1.y = t2.y = min(a.y, c.y);
        t1.x = a.x + (b.x - a.x)*(t1.y - a.y)/(b.y-a.y);
        t2.x = c.x + (d.x - c.x)*(t2.y - c.y)/(d.y-c.y);
        double ans = fabs((t1.x - t2.x) * (t1.y-p.y)/2.0);
        printf("%.2f\n", ans+eps); //控制精度， 
    }
    return 0;
}