[论文笔记] ：Temporal Graph Networks for Deep Learning on Dynamic Graphs

 

 本篇文章发表在ICLR2020上，对动态图的进行连接预测和结点分类。TGN中，作者除利用传统的图神经网络捕捉非欧式结构生成embedding外，还利用动态图所中时序信息。

 

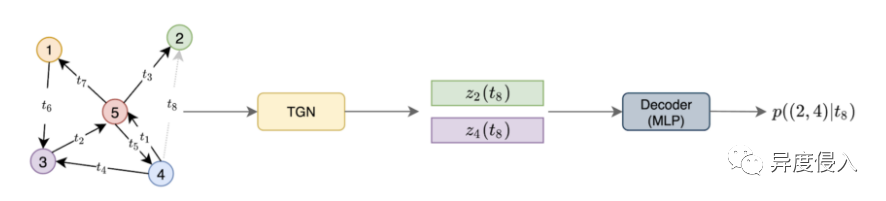
 TGN主要是由编码器和解码器构成，其中编码器负责将动态网络的每个结点编码成一个向量，解码器会根据具体的训练问题对编码后的向量计算预测属性值，最后根据decoder得到的值设计损失函数，通过优化损失函数来对整个网络进行优化。

先说一下TGN方法的细节：

 

 

 

 

 

 

 

 

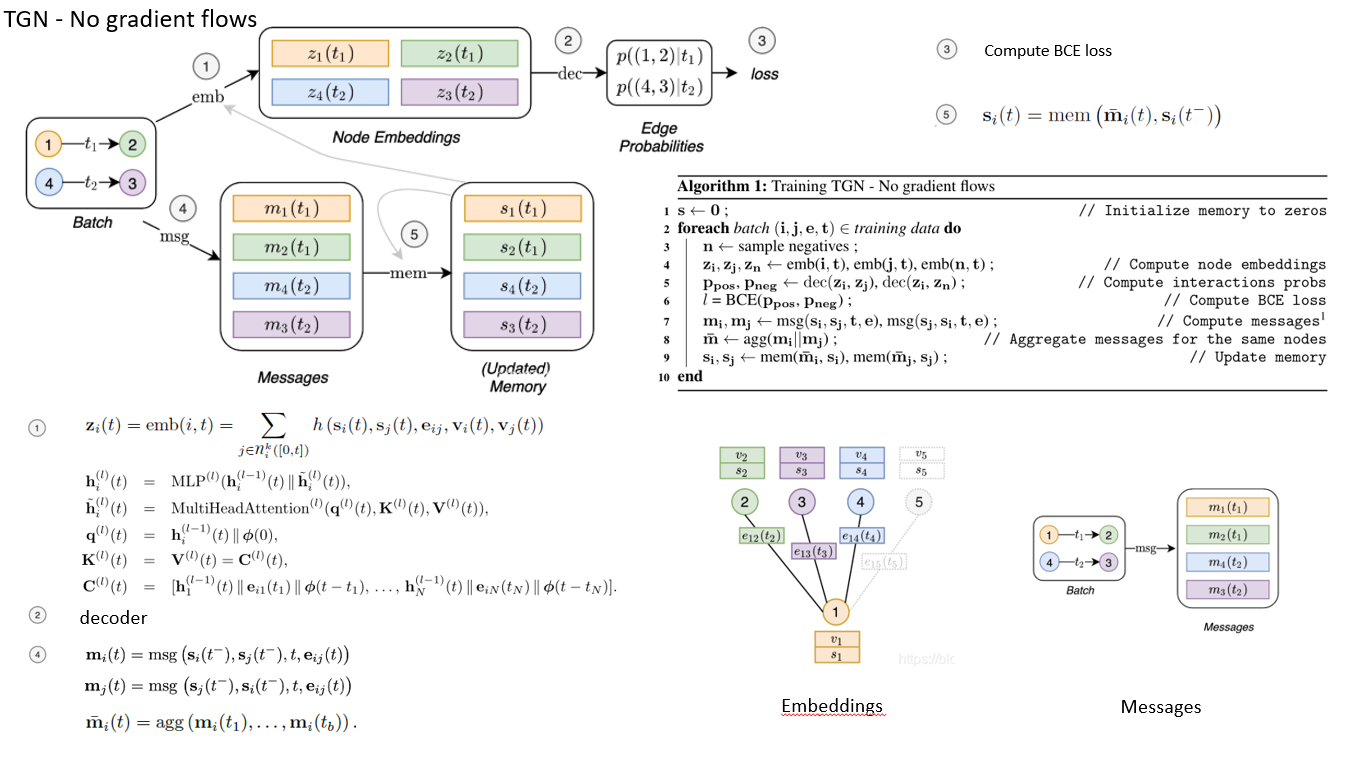
 上面两页是概述，下面是细节：

 

按照论文的顺序，先介绍一下背景，在静态图中的深度学习常通过邻居节点的信息传递函数来做到

 

 

 懒得重新敲公式了，直接摘了一段自己写在word里的总结。。。。忽略建图的背景

 

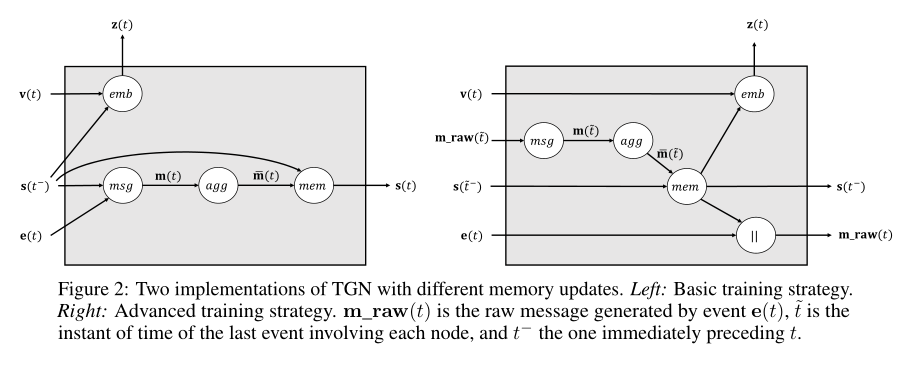
 有了以上两个背景，提出了本文的动态神经网络的整体流程图

 

 

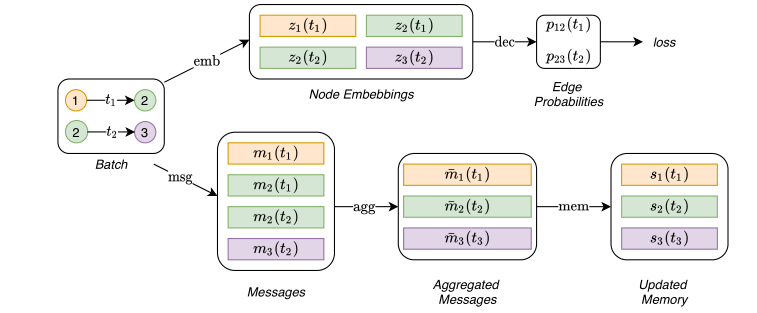
我们分块来讲，

Messages: 

 Messages Function: 对于涉及节点i的每个事件，都会计算一条消息以更新i的内存。对于在时间t的节点i和j之间的交互事件eij（t），可以为分别开始和接收交互的源节点和目标节点计算两条消息：

 

 

 同样，在节点事件vi（t）的情况下，可以为该事件所涉及的节点计算一条消息：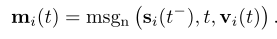

 

 

 在这里，si（t-）是节点i在时间t之前的内存，而msgs，msgd和msgnare是可学习的消息函数，例如MLP。在我们所有的实验中，为简单起见，我们选择消息函数作为标识（id），它只是输入的串联.

 Messages Aggregator

由于效率原因而诉诸批处理(batch)，但可能会导致涉及同一批中同一节点i的多个事件。当每个事件在我们的公式中生成一条消息时，我们使用一种机制来聚合消息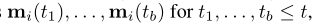

 

 

 

 

 

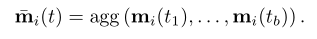
 在这里，agg是一个聚合函数。尽管可以考虑多种选择来实现此模块（例如，RNN或对节点内存的关注），但为简单起见，我们在实验中考虑了两种有效的不可学习的解决方案：最新消息（对于给定的消息仅保留最新消息）节点）和平均消息（平均给定节点的所有消息）。我们将可学习的聚合作为未来的研究方向。

Memory : 模型的内存（状态）由模型迄今所见的每个节点的向量si（t）组成。当节点涉及事件时（例如与另一个节点的交互或逐节点变化），节点的存储器被更新，并且其目的是以压缩格式表示节点的历史。多亏了这个特定的模块，TGN才能够记住图中每个节点的长期依赖关系。另外，可以将全局存储器添加到模型中以跟踪整个时间网络的演变。虽然我们设想了这种内存可能带来的好处（例如，信息可以轻松地在图形中传播很长一段距离，但是可以通过全局状态的变化来更新节点的内存，可以轻松地基于全局内存进行基于图形的预测），这样的方向没有在这项工作中进行探索，因此留待将来的研究。

Memory Updater :节点的内存在涉及节点本身的每个事件时都会更新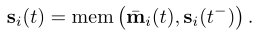：对于涉及两个节点i和j的交互事件，事件发生后将更新两个节点的内存。对于节点事件，仅更新相关节点的内存。在此，mem是可学习的内存更新功能，例如递归神经网络，例如LSTM [29]或GRU

 

 

 

 Embedding : 

嵌入模块用于在任何时间t生成节点i的时间嵌入zi（t）。嵌入模块的主要目的是避免所谓的staleness问题。由于节点i的内存仅在节点参与事件时才更新，因此可能会发生以下情况：长时间不存在事件（例如，社交网络用户在活跃之前停止使用平台一段时间）再次），我的记忆变得陈旧。尽管可以实现嵌入模块的多种实现，但我们使用以下形式：

 

 

 

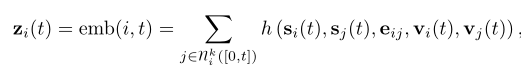
其中h是一个可学习的函数。在特定情况下，这包括许多不同的公式：

　　Identity（id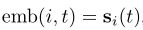）：，它直接使用内存作为节点嵌入。

　　Time projection (time)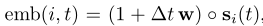：，其中w是可学习的参数，∆t是自上一次交互以来的时间，而◦表示逐元素矢量积。此版本的嵌入方法已在JODIE中使用。

　　Temporal Graph Attention (attn)：一系列L图注意层通过汇总来自其L跳时间邻域的信息来计算i的嵌入。第l层的输入是i表示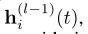，当前时间戳t，i邻域表示以及时间戳下对于在i的时间邻域中形成边的每个考虑的相互作用，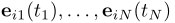

　　　　

 在此，φ（·）表示通用时间编码，k是级联运算符，zi（t）= emb（i，t）= h（L）i（t）。每层相当于执行多头注意[60]，其中查询（q（l）（t））是参考节点（即目标节点或其L-1跳近邻之一），而密钥K （l）（t）和值V（l）（t）是其邻居。最后，使用MLP将参考节点表示形式与聚合信息组合在一起。与该层的原始公式（首先在TGAT中提出）不同，在此情况下，不使用节点级时态特征，在本例中，每个节点的输入表示为h（0）j（t）= sj（t）+ vj（t），因此它允许模型利用当前内存sj（t）和时间节点特征vj（t）。

　　Temporal Graph Sum (sum): 图上更简单，更快速的聚合：

 

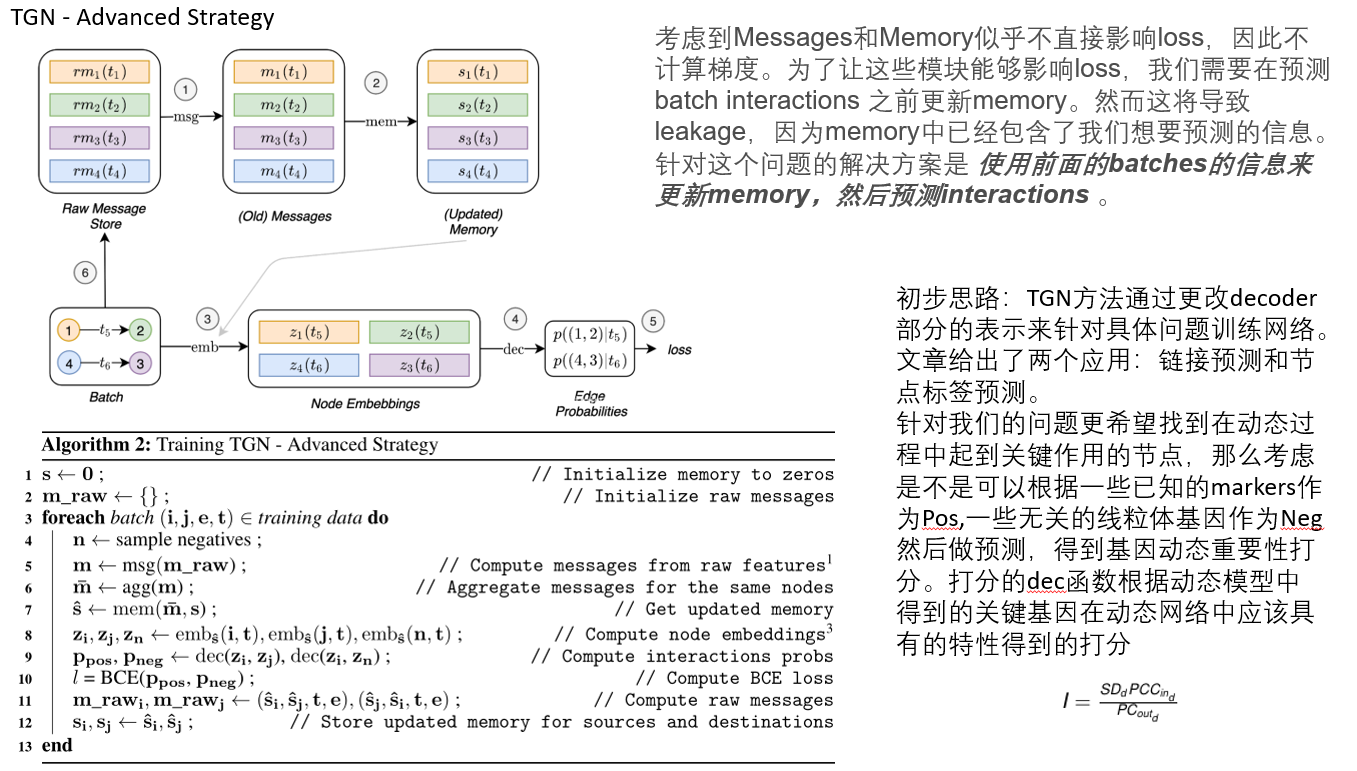
 两种训练机制：