[论文笔记] Detecting early-warning signals for sudden deterioration of complex diseases by dynamical network biomarkers
这篇文章是我不擅长的数学，所以很多地方都是我定理并没有很严格的证明。
这篇文章陈洛阳老师2012年3月发表在SCIENTIFIC REPORTS上
通过动态网络生物标记物检测复杂疾病突然恶化的预警信号，这篇文章基于的假设是很多疾病的恶化过程往往不是连续的过程而是存在突变的点，
这类似于非线性动态系统的分岔点理论中的分岔点（某个动态系统保持平衡，但在动态系统的某个参数达到一定阈值后系统状态瞬间转为不平衡的状态的点），所以似乎在要看懂这篇文章就要先介绍一下下面的一些概念：非线性动态系统不动点、分岔点理论、雅可比矩阵的理解。
我们一个个的来
1. 非线性动态系统。
非线性动态系统可以表示为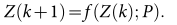
其中k为时间，p为非线性动态系统中造成特征波动的特征参数，这里z(k)为动态系统的特征值。那么为了方便后面的讲解，我们也可以将其简化写为x_t = f(x_t-1;p) . 那么这个形式如果不把参数显示的表示出来又可以简化成为
………………………………………………………………（1）
我们知道对于一个函数，它的不动点（平衡点）的含义是f(x) = x，即系统状态经过一系列变换后又回到原始状态。
那我们定义1: 如果某个非线性动态系统的一个不动点（平衡解），设通过坐标边换可以将其移到原点x_0 = 0.,那么方程（1）的平衡位置x_0 = 0称为（Lyapunov意义下）稳定的，若任给
，存在
（只依赖于
，而不依赖于t），使得从每一个
的x出发的解
，在所有的t>0上满足
定义2：方程（1）的平衡位置x_0 = 0 是渐进稳定的，若它是Lyapunov意义下稳定的，并且假定，对于零点的充分小邻域内具有初始条件
的每一个解
都有
给出一个英语对平衡态的解释
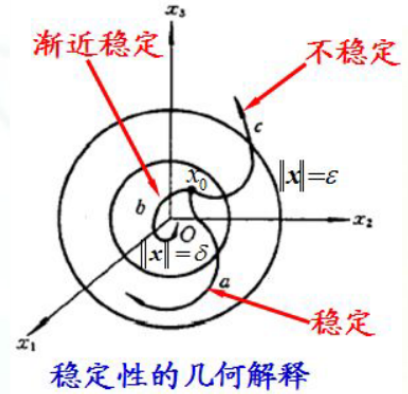
那么如何求解动态系统的平衡解，多数情况下可以通过平衡点附近的线性化系统来得到，
对于方程（1），设该系统具有平衡位置x*,即满足f(x*) = 0。 我们检验其轨道附近的稳定性，设
并设
为小量，带入（1），并将右端展开，得
由于x*为平衡解，故f(x*) = 0, 于是忽略高阶项，其中
其中：
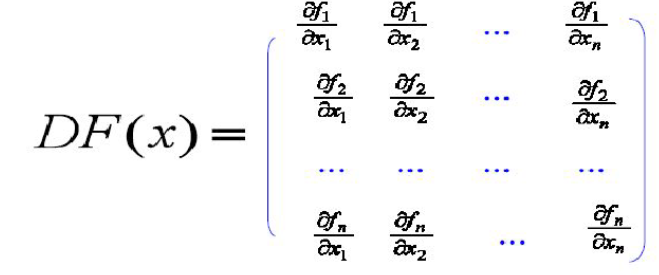
该系统为线性化系统，其不动点解
的演化多数情况下决定了系统（1）在不动点解x*的稳定性。通解为
初值为
S_k为的DF(x*)的N个特征根，于是有：
上面的定义说明了在平衡点上系统存在不同的解的性质，那么分岔理论就来了，
定义：对于一个非线性动态系统，由于其中参数取值不同，解的形式可能完全不同，即参量取值在某一临界值两侧，解的性质发生本质变化（例如平衡状态或周期运动的数目和稳定性等发生突然变化）。人们称解在此临界处发生分岔。分叉现象是非线性系统特有的一种非常重要的性质。
给出两个很好理解的例子：
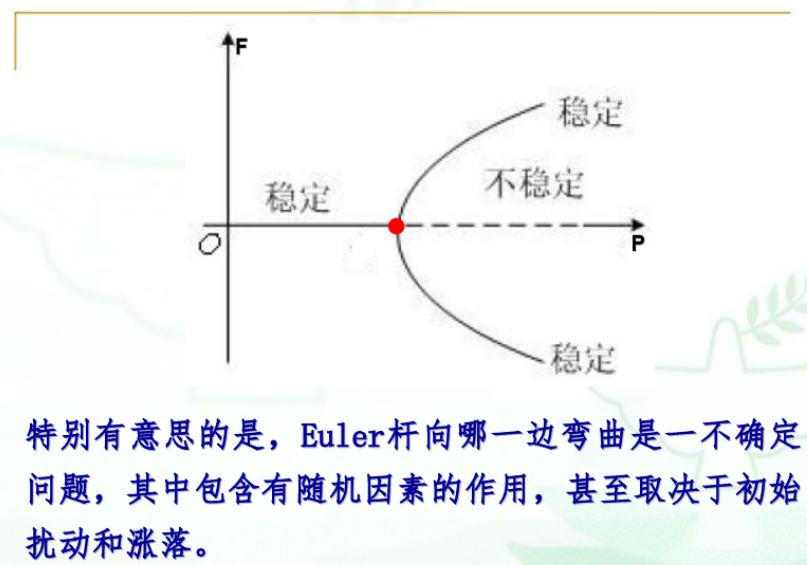
上面就是介绍了非线性动态系统的分岔理论，也给出了如何找到分岔点的数学方法，即首先计算系统的不动点（参数表示），然后计算整个系统在不动点出的雅可比矩阵的特征值（用参数表示），因为特征值的特征反应了解的特性，故可以计算参数如何变化时可以让不动点的特性发生改变。举个例子
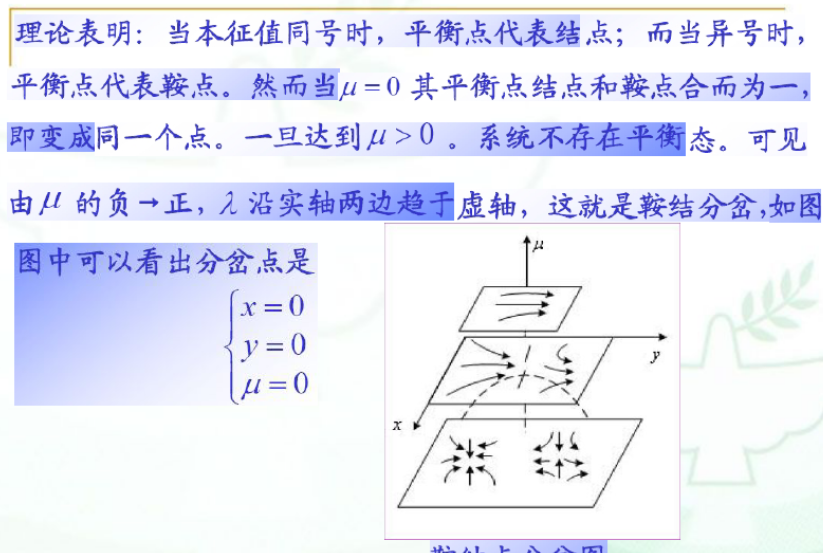
那么第三个问题，雅可比矩阵的理解，我们知道空间的线性边换可以通过矩阵表示，而非线性边可以转化为结点局部的线性变化，这就涉及到非线性函数的导数方向，那么雅可比矩阵是很好的非线性边换的转化矩阵，具体的转化方法，见传送门：https://zhuanlan.zhihu.com/p/123934469
言归正传，这篇文章中，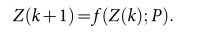
通过对P的巧妙构建，发现当P的形式符合三种形式时，系统存在分岔点，
分别为，并给出了分岔点的趋势：
综上，按照趋势合并三个形式的特征，整合为一个预测score就是变成了：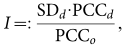
下面就可以用I的大小来衡量对整个系统的分岔点影响最大的社团，即上式中的d ; domain group.就可以得到可以预测系统是否发生相变的社团了。
给出一个写的特别明白的对分岔和混沌理论的解释
https://www.zhihu.com/question/68229746/answer/561377778 写的非常好，都是大佬，欢迎传送！
