Codeforces Round #532 (Div. 2)

终于。。

A - Roman and Browser

有很多写法，当然我也知道可以暴力，但是前缀和的写法就很舒服啊。

#include<bits/stdc++.h>
using namespace std;

char gc() {
//	static char buf[100000],*p1,*p2;
//	return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100000,stdin))?EOF:*p1++;
	return getchar();
}

template<class T>
int read(T &ans) {
	T f=1;ans=0;
	char ch=gc();
	while(!isdigit(ch)) {
		if(ch==EOF) return EOF;
		if(ch=='-') f=-1;
		ch=gc();
	}
	while(isdigit(ch))
		ans=ans*10+ch-'0',ch=gc();
	ans*=f;return 1;
}

template<class T1,class T2>
int read(T1 &a,T2 &b) {
	return read(a)==EOF?EOF:read(b);
}

template<class T1,class T2,class T3>
int read(T1 &a,T2 &b,T3 &c) {
	return read(a,b)==EOF?EOF:read(c);
}

typedef long long ll;
const int Maxn=1100000;
const int inf=0x3f3f3f3f;
const ll mod=998244353;

int n,k,a[Maxn],s[Maxn],sum,ans;

int main() {
	read(n,k);
	for(int i=1;i<=n;i++)
		read(a[i]),sum+=a[i];
	for(int i=1;i<k;i++) s[i]=a[i];
	for(int i=k;i<=n;i++) s[i]=s[i-k]+a[i];
	for(int i=n-k+1;i<=n;i++) ans=max(ans,abs(sum-s[i]));
	printf("%d",ans);
	return 0;
}

B - Build a Contest

根据题意直接模拟即可。

#include<bits/stdc++.h>
using namespace std;

char gc() {
//	static char buf[100000],*p1,*p2;
//	return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100000,stdin))?EOF:*p1++;
	return getchar();
}

template<class T>
int read(T &ans) {
	T f=1;ans=0;
	char ch=gc();
	while(!isdigit(ch)) {
		if(ch==EOF) return EOF;
		if(ch=='-') f=-1;
		ch=gc();
	}
	while(isdigit(ch))
		ans=ans*10+ch-'0',ch=gc();
	ans*=f;return 1;
}

template<class T1,class T2>
int read(T1 &a,T2 &b) {
	return read(a)==EOF?EOF:read(b);
}

template<class T1,class T2,class T3>
int read(T1 &a,T2 &b,T3 &c) {
	return read(a,b)==EOF?EOF:read(c);
}

typedef long long ll;
const int Maxn=1100000;
const int inf=0x3f3f3f3f;
const ll mod=998244353;

int n,m,x,cnt[Maxn];

int main() {
	read(n,m);
	int temp=0;
	for(int i=1;i<=m;i++) {
		read(x);
		if(cnt[x]==0)
			temp++;
		cnt[x]++;
		if(temp==n) {
			putchar('1');
			for(int i=1;i<=n;i++) {
				cnt[i]--;
				if(cnt[i]==0) temp--;
			}
		}
		else putchar('0');
	}
	putchar('\n');
	return 0;
}

C - NN and the Optical Illusion

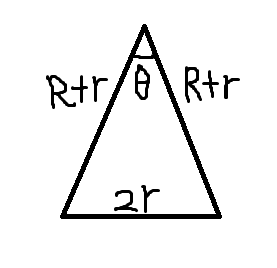
如上图，长度为2r的边就是正n边形的边，那么\(\theta = \frac{2\pi}{n}\)

那么由余弦定理知，\(c^2=a^2+b^2-2ab\cos C\)，那么这里的\(a=b=R+r,c=2r,C=\theta\)，化一下式子就出来了。

#include<bits/stdc++.h>
using namespace std;

char gc() {
//	static char buf[100000],*p1,*p2;
//	return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100000,stdin))?EOF:*p1++;
	return getchar();
}

template<class T>
int read(T &ans) {
	T f=1;ans=0;
	char ch=gc();
	while(!isdigit(ch)) {
		if(ch==EOF) return EOF;
		if(ch=='-') f=-1;
		ch=gc();
	}
	while(isdigit(ch))
		ans=ans*10+ch-'0',ch=gc();
	ans*=f;return 1;
}

template<class T1,class T2>
int read(T1 &a,T2 &b) {
	return read(a)==EOF?EOF:read(b);
}

template<class T1,class T2,class T3>
int read(T1 &a,T2 &b,T3 &c) {
	return read(a,b)==EOF?EOF:read(c);
}

typedef long long ll;
const int Maxn=1100000;
const int inf=0x3f3f3f3f;
const ll mod=998244353;
const double Pi=acos(-1);

int n,R;

int main() {
	read(n,R);
	double d=2.0*cos(2.0*Pi/n);
	double a=2.0+d,b=(4.0-2.0*d)*R,c=(2.0-d)*R*R;
	printf("%.11lf",(b+sqrt(b*b+4.0*a*c))/(2.0*a));
	return 0;
}

D - Dasha and Chess

首先把king移动到中间，然后看一下现在以king为中心的四个象限中那个里面的车最少，然后往相反的方向移。因为少的那个不会超过四分之一也就是166，那另外的三个象限纵沟至少是500个，而king移动的时候另一个人必须把这500个全部放到相反的那个象限里面，而king只会走499步，那么一定能赢。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cctype>
#define qmin(x,y) (x=min(x,y))
#define qmax(x,y) (x=max(x,y))
using namespace std;

inline char gc() {
//	static char buf[100000],*p1,*p2;
//	return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
	return getchar();
}

template<class T>
int read(T &ans) {
	ans=0;char ch=gc();T f=1;
	while(!isdigit(ch)) {
		if(ch==EOF) return -1;
		if(ch=='-') f=-1;
		ch=gc();
	}
	while(isdigit(ch))
		ans=ans*10+ch-'0',ch=gc();
	ans*=f;return 1;
}

template<class T1,class T2>
int read(T1 &a,T2 &b) {
	return read(a)!=EOF&&read(b)!=EOF?2:EOF;
}

template<class T1,class T2,class T3>
int read(T1 &a,T2 &b,T3 &c) {
	return read(a,b)!=EOF&&read(c)!=EOF?3:EOF;
}

typedef long long ll;
const int Maxn=1100;
const int inf=0x3f3f3f3f;
const int c=500;

int nx,ny,a[Maxn][Maxn],x[Maxn],y[Maxn];

void get(int X,int Y) {
	if(nx>X) nx--;
	else if(nx<X) nx++;
	if(ny>Y&&!a[nx][ny-1]) ny--;
	else if(ny<Y&&!a[nx][ny+1]) ny++;
}

void work(int X,int Y) {
	while(nx!=X||ny!=Y) {
		get(X,Y);
		printf("%d %d\n",nx,ny);
		fflush(stdout);
		int b;
		read(b);
		if(b<=-1) exit(0);
		a[x[b]][y[b]]=0;
		read(x[b],y[b]);
		a[x[b]][y[b]]=1;
	}
}

signed main() {
//	freopen("test.in","r",stdin);
	read(nx,ny);
	for(int i=1;i<=666;i++) read(x[i],y[i]),a[x[i]][y[i]]=1;
	work(c,c);
	int zhy=0;
	for(int i=1;i<=c;i++) for(int j=1;j<=c;j++) if(a[i][j]) zhy++;
	if(zhy<=166) work(999,999);zhy=0;
	for(int i=1;i<=c;i++) for(int j=c;j<=999;j++) if(a[i][j]) zhy++;
	if(zhy<=166) work(999,1);zhy=0;
	for(int i=c;i<=999;i++) for(int j=1;j<=c;j++) if(a[i][j]) zhy++;
	if(zhy<=166) work(1,999);
	work(1,1);
	return 0;
}

E - Andrew and Taxi

首先把边按权值从小到大排序，然后二分最后的发生变向的边是哪一个。

那么这条边后面的边一定都没有变向，如果这里面有环，那么就排除，然后继续二分。

最后求出来为使得后面没有环，最后的发生变向的边。显然后面的边形成一个DAG，那么求出来DAG上的拓扑序，然后对于所有的边，由拓扑序小的指向拓扑序大的即可。

#include<bits/stdc++.h>
using namespace std;

char gc() {
//	static char buf[100000],*p1,*p2;
//	return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100000,stdin))?EOF:*p1++;
	return getchar();
}

template<class T>
int read(T &ans) {
	T f=1;ans=0;
	char ch=gc();
	while(!isdigit(ch)) {
		if(ch==EOF) return EOF;
		if(ch=='-') f=-1;
		ch=gc();
	}
	while(isdigit(ch))
		ans=ans*10+ch-'0',ch=gc();
	ans*=f;return 1;
}

template<class T1,class T2>
int read(T1 &a,T2 &b) {
	return read(a)==EOF?EOF:read(b);
}

template<class T1,class T2,class T3>
int read(T1 &a,T2 &b,T3 &c) {
	return read(a,b)==EOF?EOF:read(c);
}

typedef long long ll;
const int Maxn=1100000;
const int inf=0x3f3f3f3f;
const ll mod=998244353;
const double Pi=acos(-1);

int n,m,d[Maxn],first[Maxn],nxt[Maxn],to[Maxn],tot=1,vis[Maxn],bj[Maxn];
queue<int> q;

inline void add(int u,int v) {
	to[tot]=v;
	nxt[tot]=first[u];
	first[u]=tot++;
}

int dfs(int root) {
	vis[root]=1;
	bj[root]=1;
	for(int i=first[root];i;i=nxt[i])
		if(bj[to[i]]) {
			bj[root]=0;
			return 1;
		}
		else if(dfs(to[i])) {
			bj[root]=0;
			return 1;
		}
	bj[root]=0;
	return 0;
}

struct node {
	int u,v,w,id;
}a[Maxn];

int cmp(node a,node b) {
	return a.w<b.w;
}

int main() {
	read(n,m);
	for(int i=1;i<=m;i++) {
		read(a[i].u,a[i].v,a[i].w);
		a[i].id=i;
	}
	sort(a+1,a+m+1,cmp);
	int l=1,r=m,mid=l+r>>1,ans=0;
	while(l<=r) {
		memset(first,0,sizeof(first));
		memset(vis,0,sizeof(vis));
		tot=1;int flag=0;
		for(int i=mid;i<=m;i++) add(a[i].u,a[i].v);
		for(int i=1;i<=n;i++) if(!vis[i]) {
			if(dfs(i)) {
				flag=1;
				break;
			}
		}
		if(flag)
			l=mid+1;
		else {
			r=mid-1;
			ans=mid;
		}
		mid=l+r>>1;
	}
	memset(first,0,sizeof(first));tot=1;
	for(int i=ans;i<=m;i++)
		add(a[i].u,a[i].v),d[a[i].v]++;
	for(int i=1;i<=n;i++) if(!d[i]) q.push(i);
	int cnt=0;
	while(!q.empty()) {
		int now=q.front();q.pop();
		vis[now]=++cnt;
		for(int i=first[now];i;i=nxt[i]) {
			d[to[i]]--;
			if(!d[to[i]]) q.push(to[i]);
		}
	}
	cnt=0;
	for(int i=1;i<=m;i++)
		if(vis[a[i].v]<vis[a[i].u]) d[a[i].id]=1,cnt++;
	if(!ans) ans++;
	printf("%d %d\n",a[ans-1].w,cnt);
	for(int i=1;i<=m;i++) if(d[i]) printf("%d ",i);
	return 0;
}

F - Ivan and Burgers

开始的时候想用ST表套线性基，卡了一会空间之后才发现空间复杂度是假的，于是膜拜了一下别人的神奇写法。

就是把右端点相同的询问放在一起处理，由于有了位置这个限制，那么我们贪心地一定是优先选靠右的点，未来的用处一定更大，如果你会线性基的话，看一下代码就明白了。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cctype>
#define qmin(x,y) (x=min(x,y))
#define qmax(x,y) (x=max(x,y))
using namespace std;

inline char gc() {
//	static char buf[100000],*p1,*p2;
//	return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
	return getchar();
}

template<class T>
int read(T &ans) {
	ans=0;char ch=gc();T f=1;
	while(!isdigit(ch)) {
		if(ch==EOF) return -1;
		if(ch=='-') f=-1;
		ch=gc();
	}
	while(isdigit(ch))
		ans=ans*10+ch-'0',ch=gc();
	ans*=f;return 1;
}

template<class T1,class T2>
int read(T1 &a,T2 &b) {
	return read(a)!=EOF&&read(b)!=EOF?2:EOF;
}

template<class T1,class T2,class T3>
int read(T1 &a,T2 &b,T3 &c) {
	return read(a,b)!=EOF&&read(c)!=EOF?3:EOF;
}

typedef long long ll;
const int Maxn=500001;
const int inf=0x3f3f3f3f;

int n,a[Maxn],q,l[Maxn],x,ans[Maxn],p[21],po[21];
vector<int> v[Maxn];

signed main() {
//	freopen("test.in","r",stdin);
	read(n);
	for(int i=1;i<=n;i++) read(a[i]);
	read(q);
	for(int i=1;i<=q;i++) {
		read(l[i],x);
		v[x].push_back(i);
	}
	for(int i=1;i<=n;i++) {
		int x=a[i],y=i;
		for(int j=20;j>=0;j--) if(x&(1<<j)) {
			if(!p[j]) { p[j]=x; po[j]=y; break; }
			if(po[j]<y) swap(x,p[j]),swap(y,po[j]);
			x^=p[j];
		}
		for(int j=0;j<v[i].size();j++)
			for(int k=20;k>=0;k--) if(po[k]>=l[v[i][j]])
				qmax(ans[v[i][j]],ans[v[i][j]]^p[k]);
	}
	for(int i=1;i<=q;i++) printf("%d\n",ans[i]);
	return 0;
}