C# 实现 任意多边形切割折线算法
1. 内容简介
本文旨在解决任意多边形切割折线，获取切割之后的折线集合。
本文实现的算法内容包括：判断两条线段是否相交,如若相交，获取交点集合、对线上的点集，按斜率方向排序、判断点是否在多边形内、获取线段和任意多边形的交点集合、中点算法、获取任意多边形裁剪折线的线段集合。
2. 效果实现
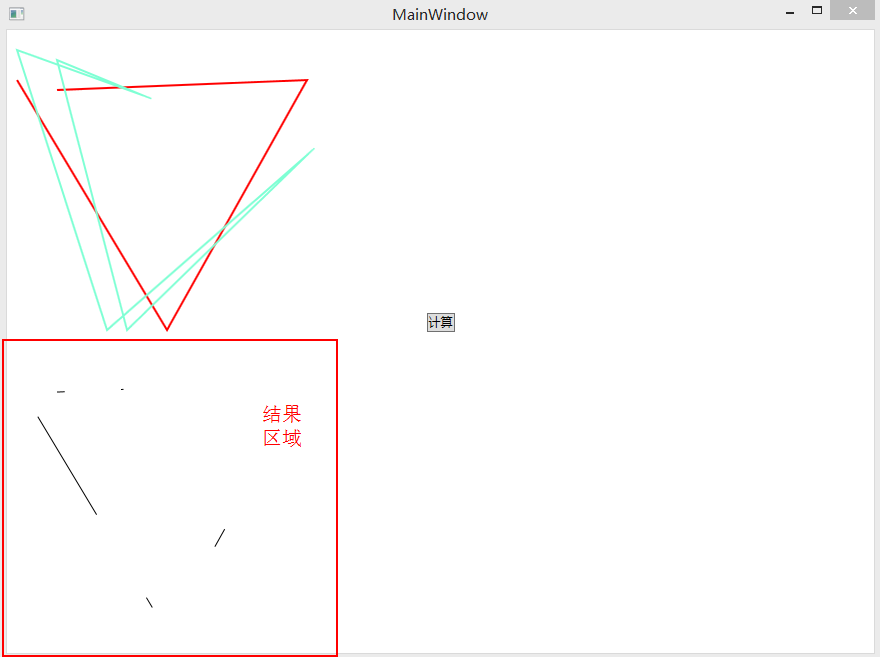
3. 算法实现
a) 本文使用到的命名空间
using System; using System.Collections.Generic; using System.Linq; using System.Windows; using System.Windows.Shapes;
b) 源代码实现
public partial class Help { #region 线段与多边形的交点集合，按从p1到p2的方向进行排序 /// <summary> /// 对一线段与多边形的交点集合，按从p1到p2的方向进行排序 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <param name="interPoints"></param> /// <returns></returns> public List<Point> SortPointsBySlopeOfLine(Point p1, Point p2, List<Point> interPoints) { List<Point> points = new List<Point>(); List<Point> newInterPoints = new List<Point>(); points.Add(p1); if (Equals(p1.X, p2.X))//垂直线段 { if (p1.Y > p2.Y) { newInterPoints = interPoints.OrderByDescending(t => t.Y).ToList(); } else { newInterPoints = interPoints.OrderBy(t => t.Y).ToList(); } } else { if (Equals(p1.Y, p2.Y))//水平线段 { if (p1.X > p2.X) { newInterPoints = interPoints.OrderByDescending(t => t.X).ToList(); } else { newInterPoints = interPoints.OrderBy(t => t.X).ToList(); } } else//普通斜率线段，按x或y都行 { if (p1.X > p2.X) { newInterPoints = interPoints.OrderByDescending(t => t.X).ToList(); } else { newInterPoints = interPoints.OrderBy(t => t.X).ToList(); } } } foreach (Point interPoint in newInterPoints) { points.Add(interPoint); } points.Add(p2); return points; } #endregion #region 获取线段和线段的交点 private double eps = 1e-8; /// <summary> /// 判断一个数值是否在误差范围内 /// </summary> /// <param name="x"></param> /// <returns></returns> private bool zero(double x) { return (((x) > 0 ? (x) : -(x)) < eps); } /// <summary> /// 计算交叉乘积(P1-P0)x(P2-P0) /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <param name="p0"></param> /// <returns></returns> private double xmult(Point p1, Point p2, Point p0) { return (p1.X - p0.X) * (p2.Y - p0.Y) - (p2.X - p0.X) * (p1.Y - p0.Y); } /// <summary> /// 判点是否在线段上,包括端点 /// </summary> /// <param name="p"></param> /// <param name="l1"></param> /// <param name="l2"></param> /// <returns></returns> private bool dot_online_in(Point p, Point l1, Point l2) { return zero(xmult(p, l1, l2)) && (l1.X - p.X) * (l2.X - p.X) < eps && (l1.Y - p.Y) * (l2.Y - p.Y) < eps; } /// <summary> /// 判两点在线段同侧,点在线段上返回0 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <param name="l1"></param> /// <param name="l2"></param> /// <returns></returns> private bool same_side(Point p1, Point p2, Point l1, Point l2) { return xmult(l1, p1, l2) * xmult(l1, p2, l2) > eps; } /// <summary> /// 判断两直线平行 /// </summary> /// <param name="u1"></param> /// <param name="u2"></param> /// <param name="v1"></param> /// <param name="v2"></param> /// <returns></returns> private bool parallel(Point u1, Point u2, Point v1, Point v2) { return zero((u1.X - u2.X) * (v1.Y - v2.Y) - (v1.X - v2.X) * (u1.Y - u2.Y)); } /// <summary> /// 判三点共线 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <param name="p3"></param> /// <returns></returns> private bool dots_inline(Point p1, Point p2, Point p3) { return zero(xmult(p1, p2, p3)); } /// <summary> /// 判两线段相交,包括端点和部分重合 /// </summary> /// <param name="u1"></param> /// <param name="u2"></param> /// <param name="v1"></param> /// <param name="v2"></param> /// <returns></returns> private bool intersect_in(Point u1, Point u2, Point v1, Point v2) { if (!dots_inline(u1, u2, v1) || !dots_inline(u1, u2, v2)) return !same_side(u1, u2, v1, v2) && !same_side(v1, v2, u1, u2); return dot_online_in(u1, v1, v2) || dot_online_in(u2, v1, v2) || dot_online_in(v1, u1, u2) || dot_online_in(v2, u1, u2); } /// <summary> /// 计算两线段交点,请判线段是否相交(同时还是要判断是否平行!) /// </summary> /// <param name="u1"></param> /// <param name="u2"></param> /// <param name="v1"></param> /// <param name="v2"></param> /// <param name="ret"></param> /// <returns></returns> private int GetIntersectionPoint(Point u1, Point u2, Point v1, Point v2, out Point ret) { ret = u1; if (parallel(u1, u2, v1, v2) || !intersect_in(u1, u2, v1, v2)) { return 0; } double t = ((u1.X - v1.X) * (v1.Y - v2.Y) - (u1.Y - v1.Y) * (v1.X - v2.X)) / ((u1.X - u2.X) * (v1.Y - v2.Y) - (u1.Y - u2.Y) * (v1.X - v2.X)); ret.X += (u2.X - u1.X) * t; ret.Y += (u2.Y - u1.Y) * t; return 1; } #endregion #region 多边形包含点 /// <summary> /// 判断多边形是否包含某个点 /// </summary> /// <param name="poly">多边形边框上每个角的点坐标数组</param> /// <param name="p">要进行判断的点</param> /// <returns>true:包含; false:不包含</returns> public bool InPoly(Polygon polygon, Point p) { Point[] poly = polygon.Points.ToArray(); int i = 0, f = 0; double xi = 0, a = 0, b = 0, c = 0; Point ps, pe; ///遍历每一个点 /// Microsoft.VisualBasic.Information.UBound 获取最大下标，等同于 poly.Count-2 for (i = 0; i <= Microsoft.VisualBasic.Information.UBound(poly, 1); i++) { ps = poly[i]; if (i < Microsoft.VisualBasic.Information.UBound(poly, 1)) { pe = poly[i + 1]; } else { pe = poly[0]; } GetStdLine(ps, pe, ref a, ref b, ref c); if (a != 0) { xi = 0 - ((b * p.Y + c) / a); if (xi == p.X) { return true; } else if (xi < p.X) { f = f + Sgn(pe.Y - p.Y) - Sgn(ps.Y - p.Y); } } } return f != 0; } /// <summary> /// 根据两个点的坐标求经过两点的直线的标准方程参数A、B、C /// </summary> /// <param name="ps"></param> /// <param name="pe"></param> /// <param name="a"></param> /// <param name="b"></param> /// <param name="c"></param> private void GetStdLine(Point ps, Point pe, ref double a, ref double b, ref double c) { double xs, ys, xe, ye; double p1, p2; xs = ps.X; ys = ps.Y; xe = pe.X; ye = pe.Y; p1 = (xs * ye); p2 = (xe * ys); if (p1 == p2) { if (xs == 0) { if (xe == 0) { a = 1; b = 0; c = 0; } else if (ys == 0) { a = ye; b = 0 - xe; c = 0; } } else if (ye == 0) { if (ys == 0) { a = 0; b = 1; c = 0; } else if (xe == 0) { a = 0 - ys; b = xs; c = 0; } } } else { a = (ys - ye) / (p1 - p2); c = 1; if (ys == 0) { if (ye == 0) { b = 1; c = 0; } else { b = 0 - ((a * xe + 1) / ye); } } else { b = 0 - ((a * xs + 1) / ys); } } } private int Sgn(double a) { if (a == 0) { return 0; } else if (a < 0) { return -1; } else { return 1; } } #endregion /// <summary> /// 求出线段和多边形的交点,不包括p1p2 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <param name="polygon"></param> /// <returns></returns> public List<Point> GetInterPoints(Point p1, Point p2, Polygon polygon) { List<Point> interPoints = new List<Point>(); List<Point> polygonPoints = polygon.Points.ToList(); for (int i = 0; i < polygonPoints.Count; i++) { Point polygon1 = polygonPoints[i]; Point polygon2 = new Point(); if (i == polygonPoints.Count - 1) { polygon2 = polygonPoints[0]; } else { polygon2 = polygonPoints[i + 1]; } Point inter = new Point(); int interType = GetIntersectionPoint(p1, p2, polygon1, polygon2, out inter); switch (interType) { case 1: if (!Equals(inter, p1) && !Equals(inter, p2)) { interPoints.Add(inter); } break; case 0: default: break; } } return interPoints; } /// <summary> /// 取两个点的中点 /// </summary> /// <param name="p1"></param> /// <param name="p2"></param> /// <returns></returns> public Point GetCenter(Point p1, Point p2) { return new Point((p1.X + p2.X) / 2, (p1.Y + p2.Y) / 2); } /// <summary> /// 获取多边形裁剪折线形成的线段集合 /// </summary> /// <param name="polyline"></param> /// <param name="polygon"></param> /// <returns></returns> public List<Polyline> GetInterPolylines(Polyline polyline, Polygon polygon) { List<Polyline> list = new List<Polyline>(); //TODO： 1.遍历折线上的每相邻的两个个点，组成线段，与多边形的每一条边计算，求出此线段与多边形的边的交点 //TODO: 2.对此线段的上的交点进行排序，组成连续点的折线，判断这些线段在多边形内部的部分，加入集合 List<Point> polinePoints = polyline.Points.ToList(); List<Point> polygonPoints = polygon.Points.ToList(); for (int i = 0; i < polinePoints.Count - 1; i++) { Point one = polinePoints[i]; Point two = new Point(); if (i == polinePoints.Count - 1) { } else { two = polinePoints[i + 1]; } List<Point> inters = GetInterPoints(one, two, polygon); List<Point> sortInters = SortPointsBySlopeOfLine(one, two, inters); for (int j = 0; j < sortInters.Count; j++) { if (j < sortInters.Count - 1) { if (InPoly(polygon, GetCenter(sortInters[j], sortInters[j + 1]))) { Polyline interPolyline = new Polyline(); interPolyline.Points.Add(sortInters[j]); interPolyline.Points.Add(sortInters[j + 1]); list.Add(interPolyline); } } } } return list; } }
