B-tree
2-3 Tree
二叉搜索树的每个节点只带有一个值,这个值将数据区间划分成两部分,值左边的部分(也就是小于这个值的数据)保存到节点的左子树,值右边的部分保存到节点的右子树。因此,每个非叶子节最多能够拥有两个子节点。
如果每个节点保存两个值,那么这两个值可以将数据区间划分成三部分,左边部分的数据保存在左子树,右边部分的数据保存在右子树,介于两个值之间的那部分数据保存在中间子树。也就是说,在一个节点保存两个值的情况下,这个节点有三个子节点。
节点可以存储1个或者2个值的搜索树,就是2-3树了。二叉搜索树的查找效率为O(h),h为树的高度。在最好的情况下(完全平衡),有N个节点的二叉搜索树的高度为h=log(N),但添加删除节点时二叉搜索树容易失去平衡,失去平衡后树的高度就会发生变化,最差情况下,树的高度为N。使用平衡算法来平衡二叉搜索树,又需要花费额外的开销。
2-3树在插入数据过程中,会自动平衡。二叉搜索树的新节点只能作为叶子节点添加,而添加叶子节点提高了增加树高度的概率;二叉搜索树的根节点一旦确定就不会再被修改,直观地想下,如果根节点的值在数据区间的两端,那么最终肯定会导致树的非常不平衡。另一方面,因为二叉搜索树的节点只能保存一个值,同2-3树可以最多保存2个值相比,即使在都完全平衡的情况下,2-3树的高度也要小。
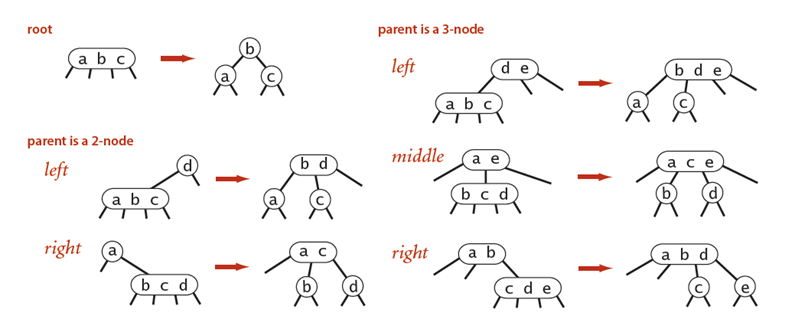
2-3树插入新节点时,如果插入点已经存在2个值,那么它首先将新值和原来的2个值放在一起构成3个值的节点,然后将这三个值的中间值向上提到父节点, 而剩余的两个值变成了父节点的两个子节点(因为分别在中间值的左右两边)。父节点也做相同的处理,依次向上提,直到根节点, 如果根节点已经为2个值的节点,那么就会改变根节点的值。这种“将中间值向上提”的过程,实际就是自动平衡的过程。
2-3树的最差查找效率为lgN,最好查找效率为log3N,约等于0.631lgN。
本节主要参考浅谈算法和数据结构:平衡查找树之2-3树
B-tree
本节主要参考MySQL索引背后的数据结构及算法原理
----------------------------------------------- 独学而无友,则孤陋而寡闻
-----------------------------------------------


