【数据结构和算法】【体系化学习】图

一、图的概念

 

 

 

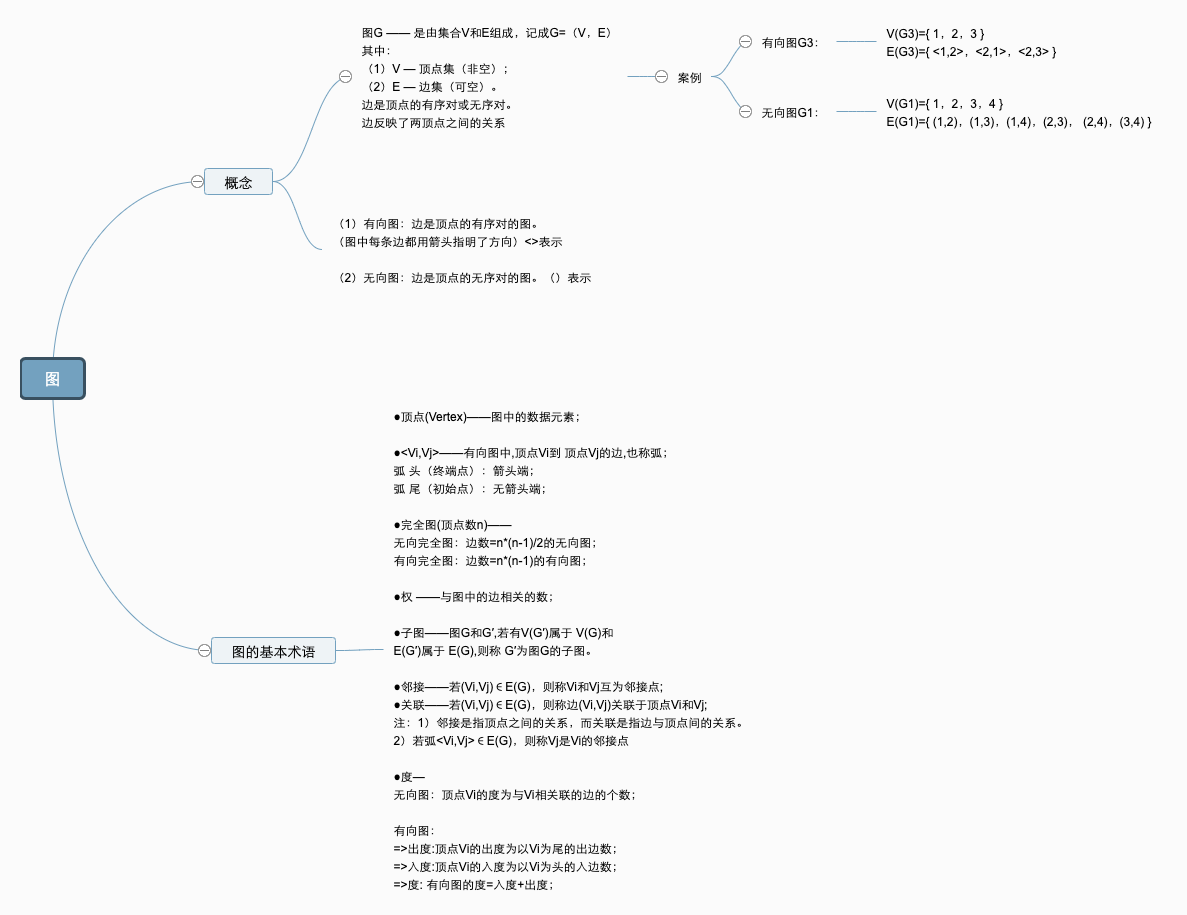
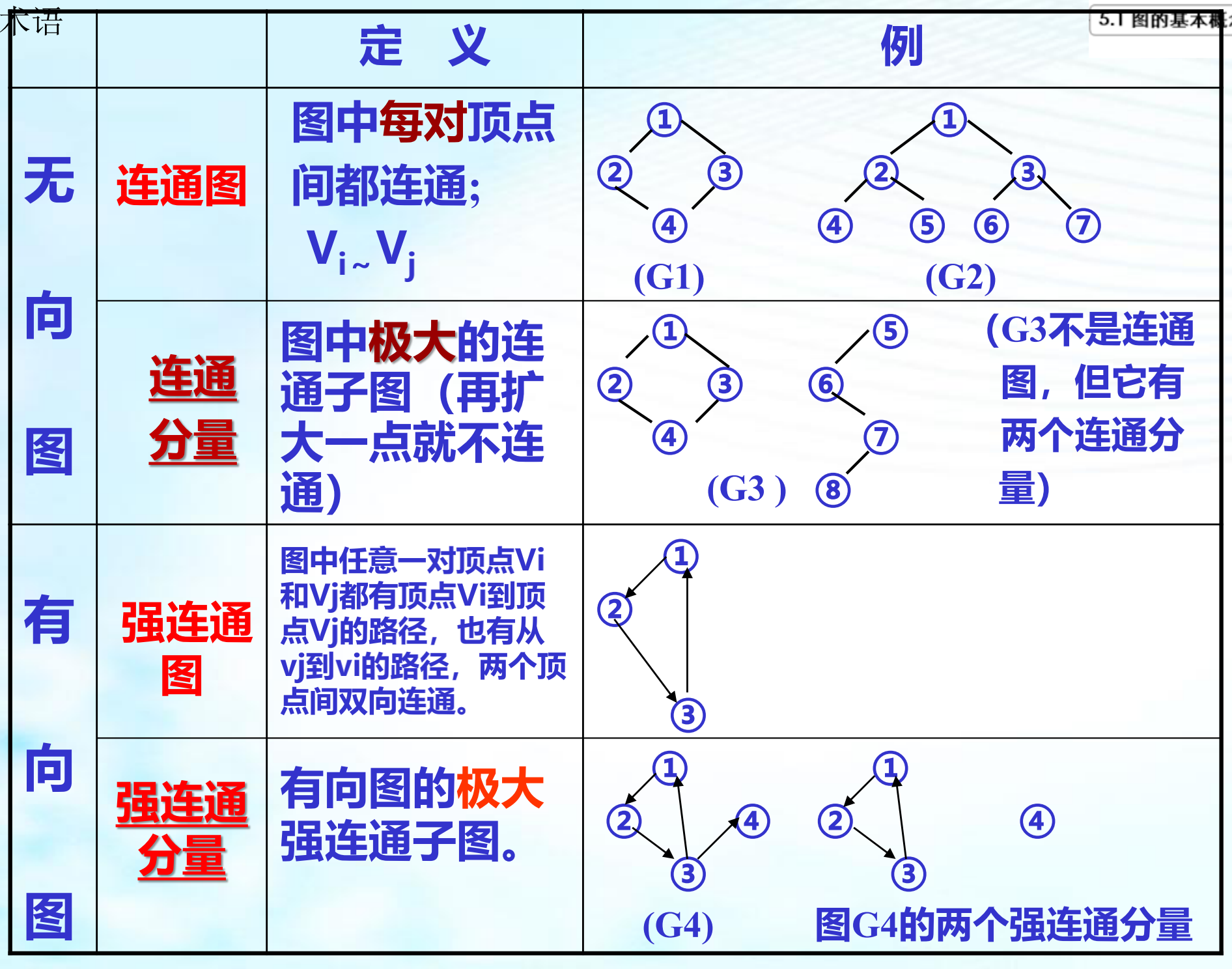
二、图的存储

 

2.1、邻接矩阵

 

 

 

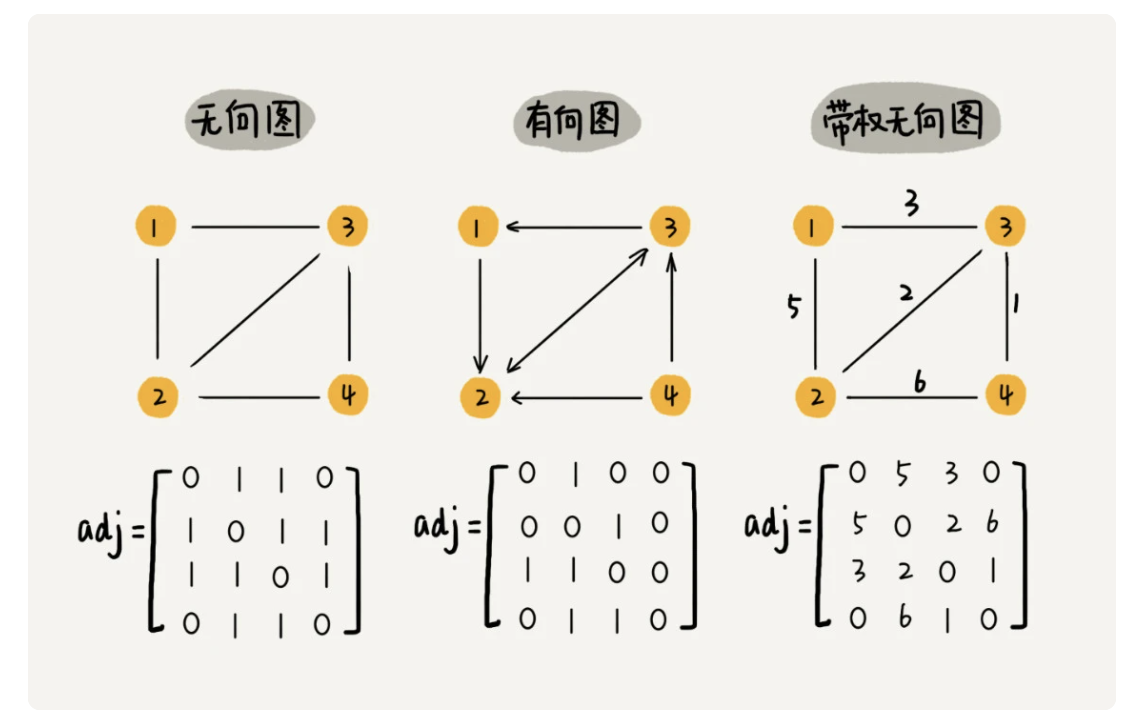
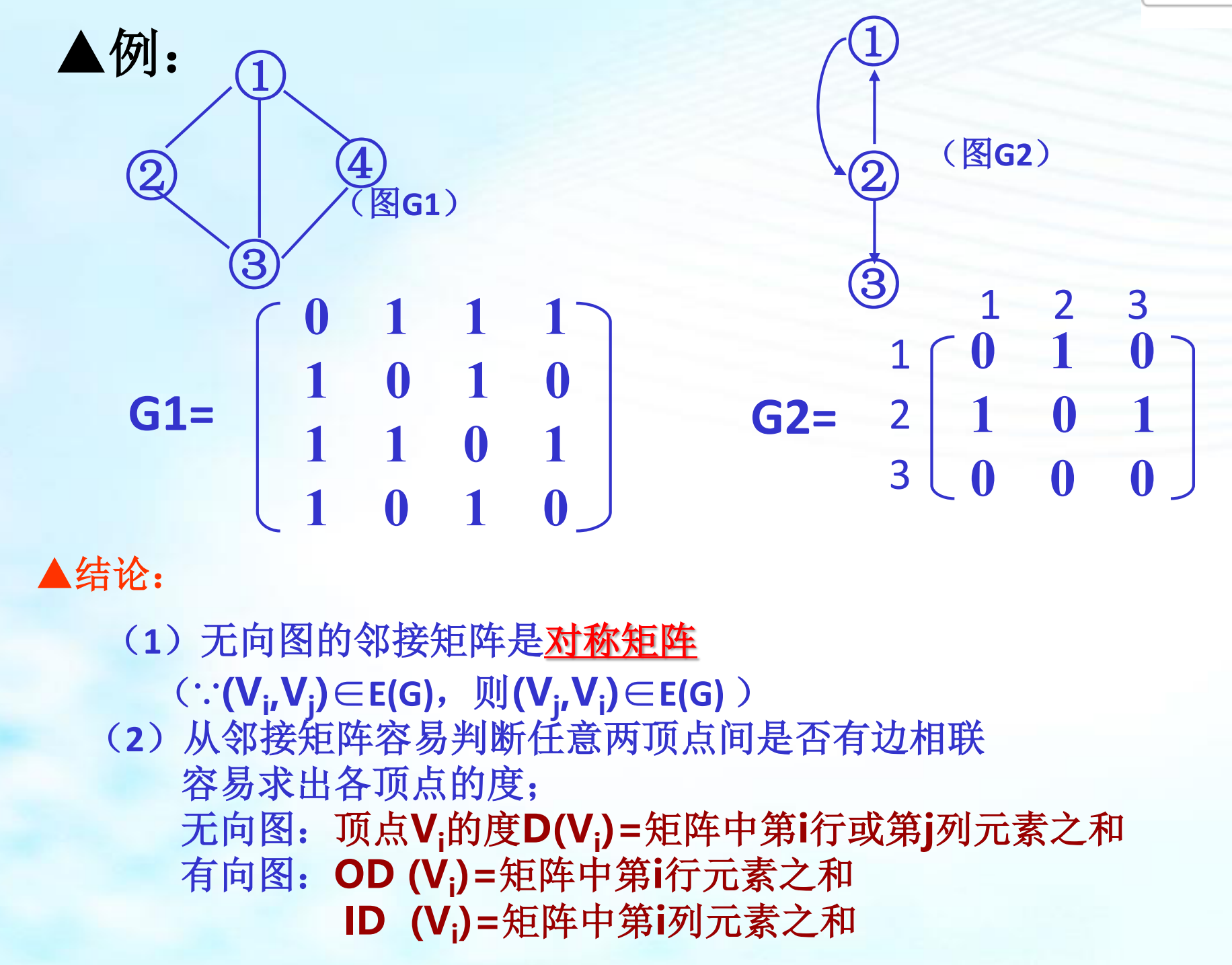
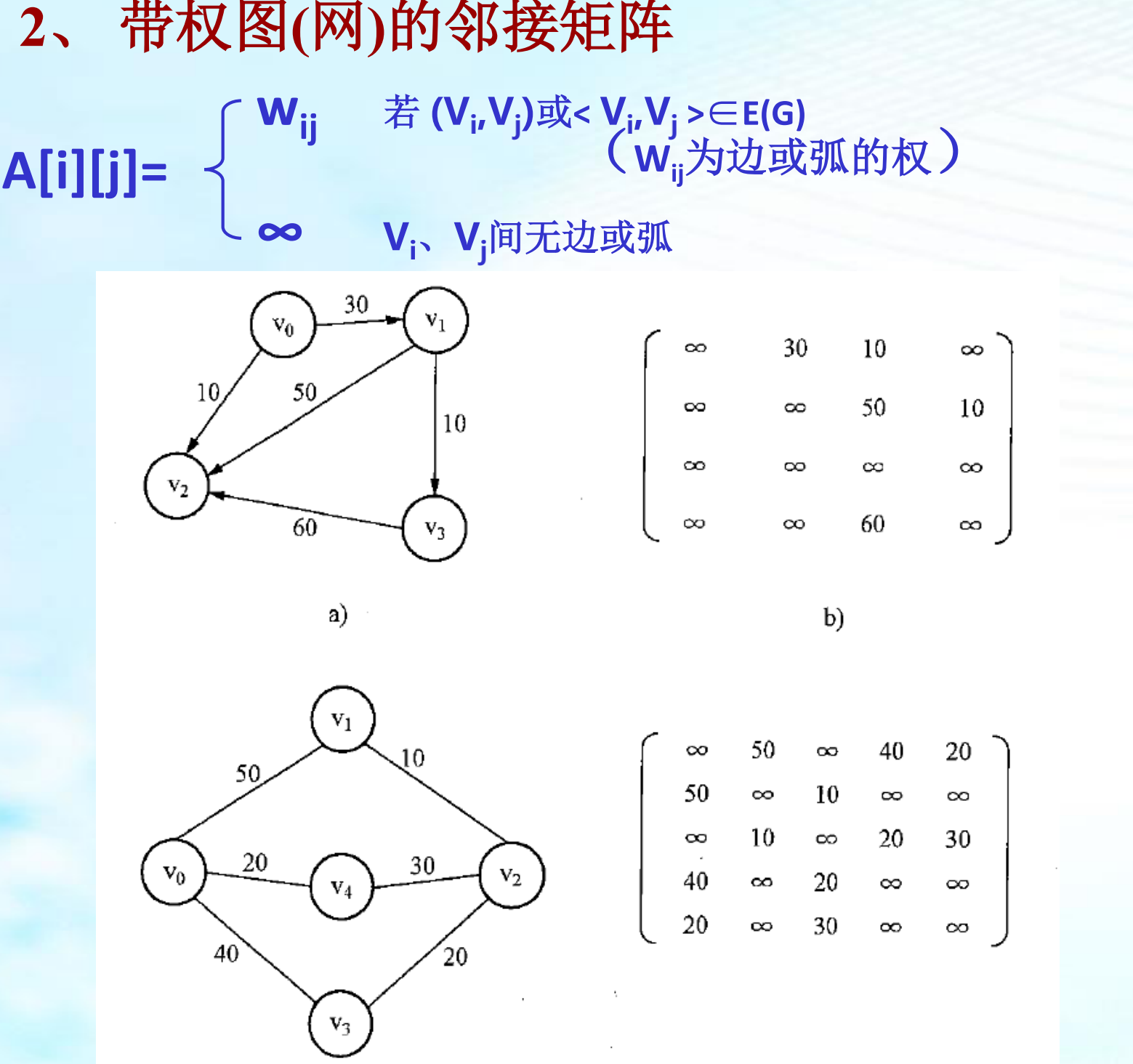
2.2、邻接表

 

 

 

 

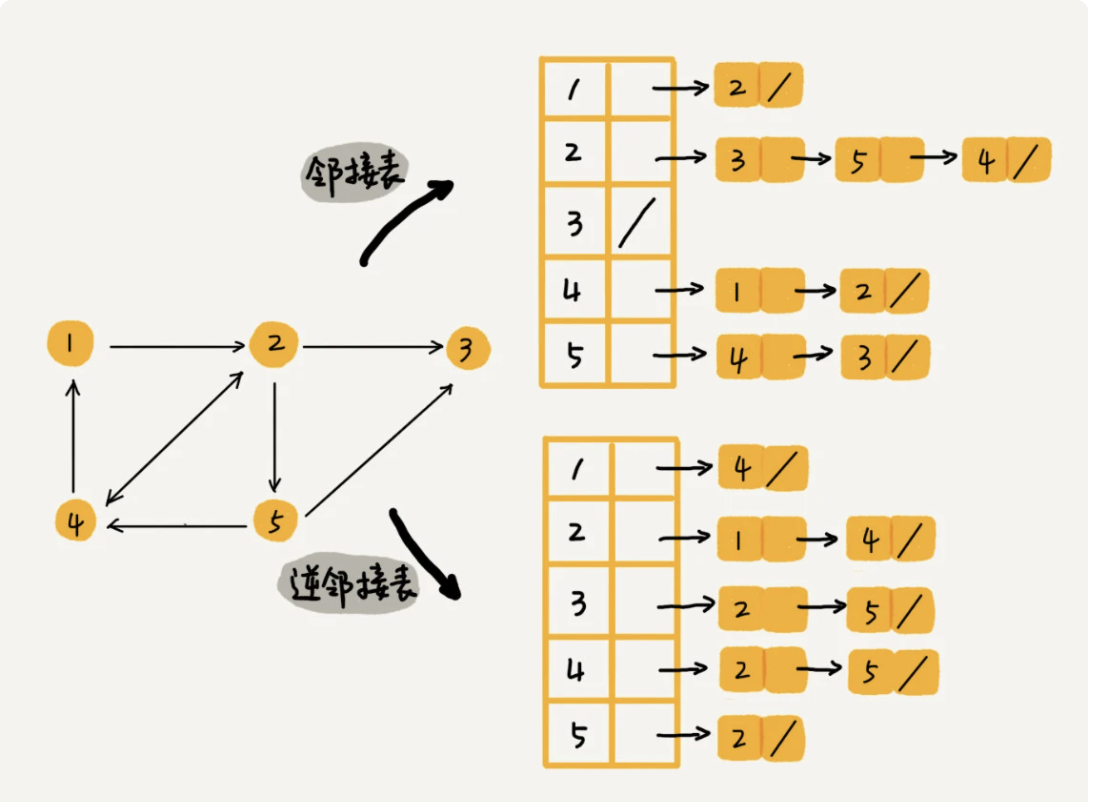
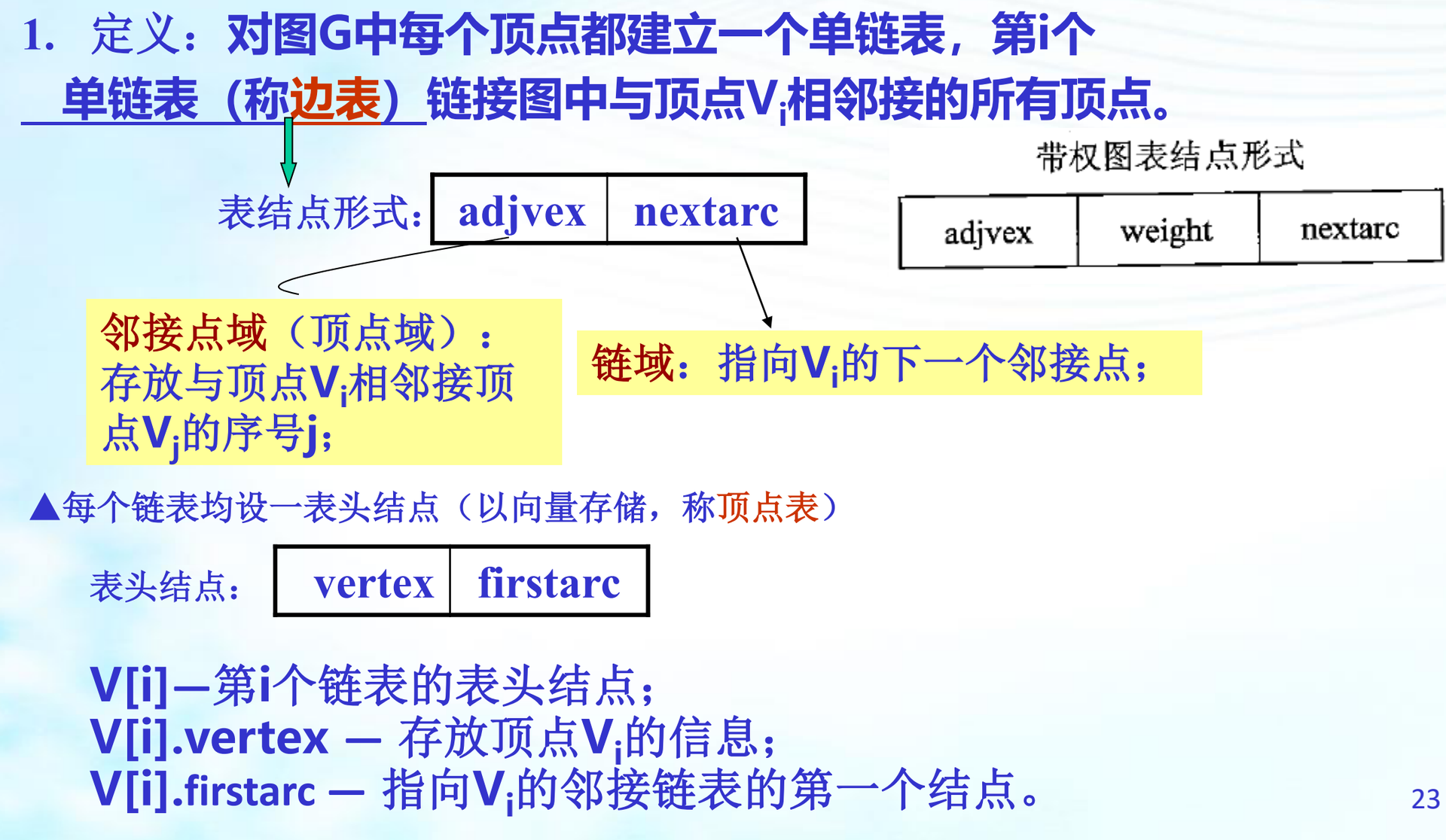
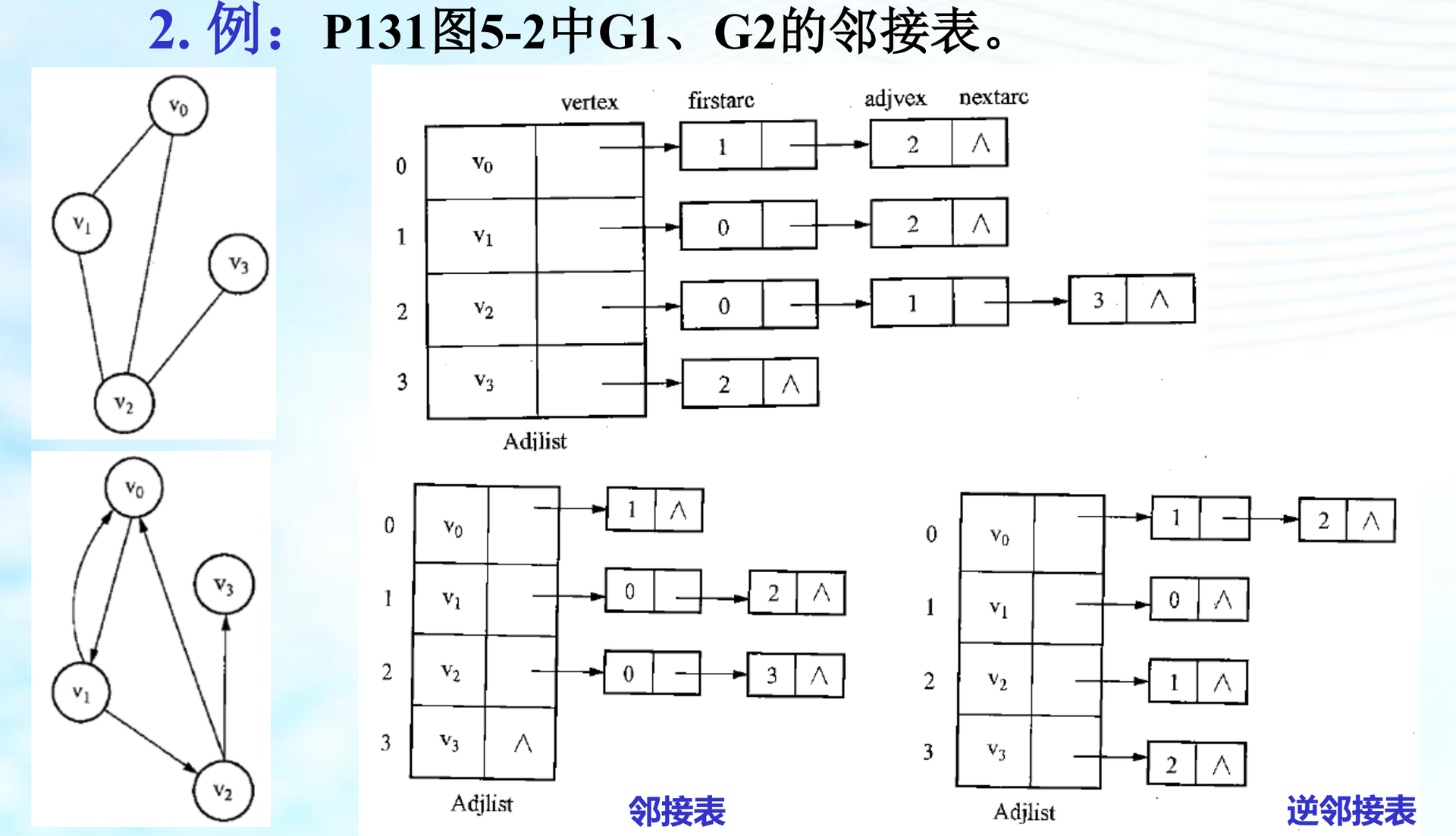
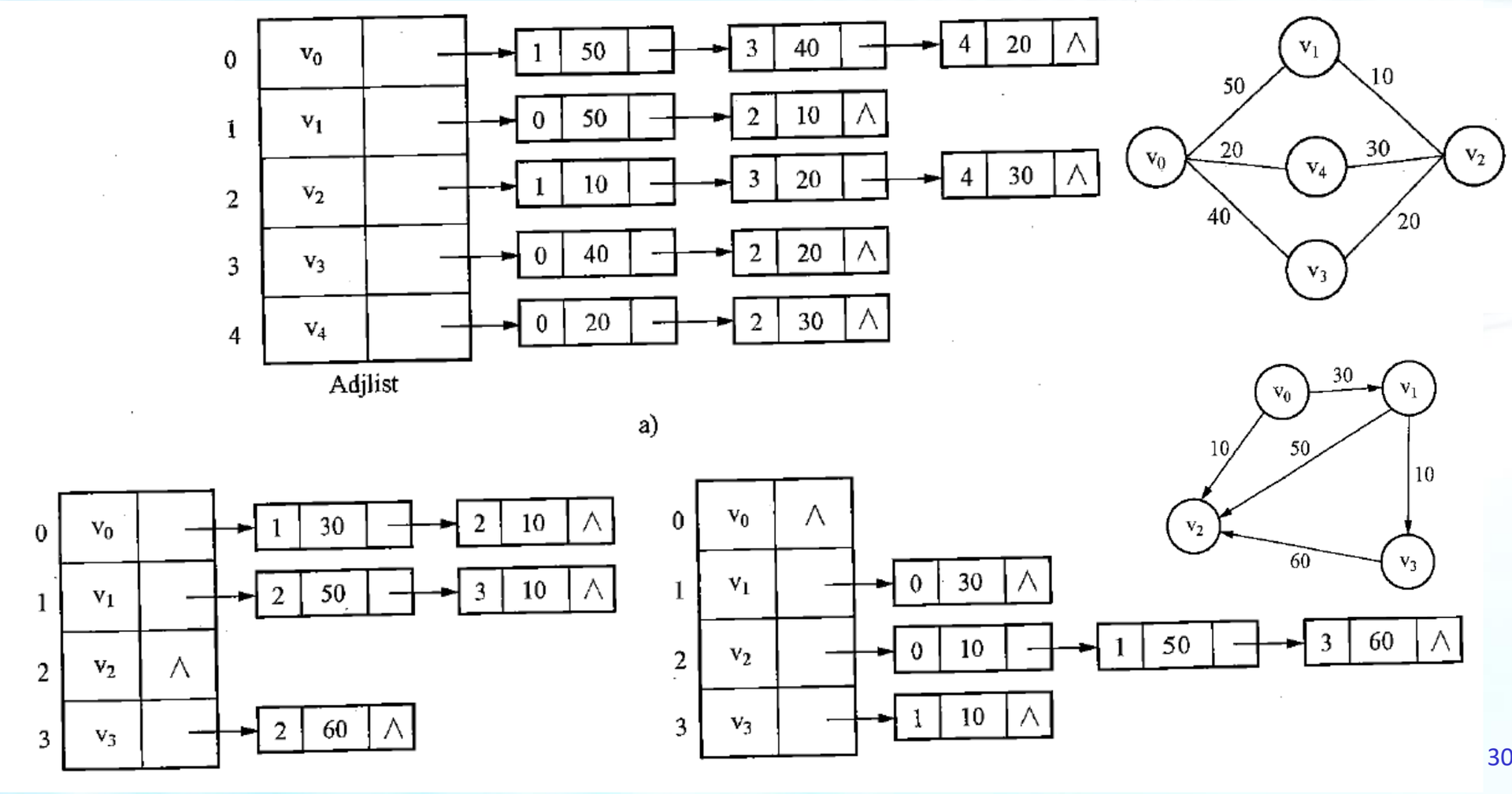
2.3、hash分片存储顶点关系

 

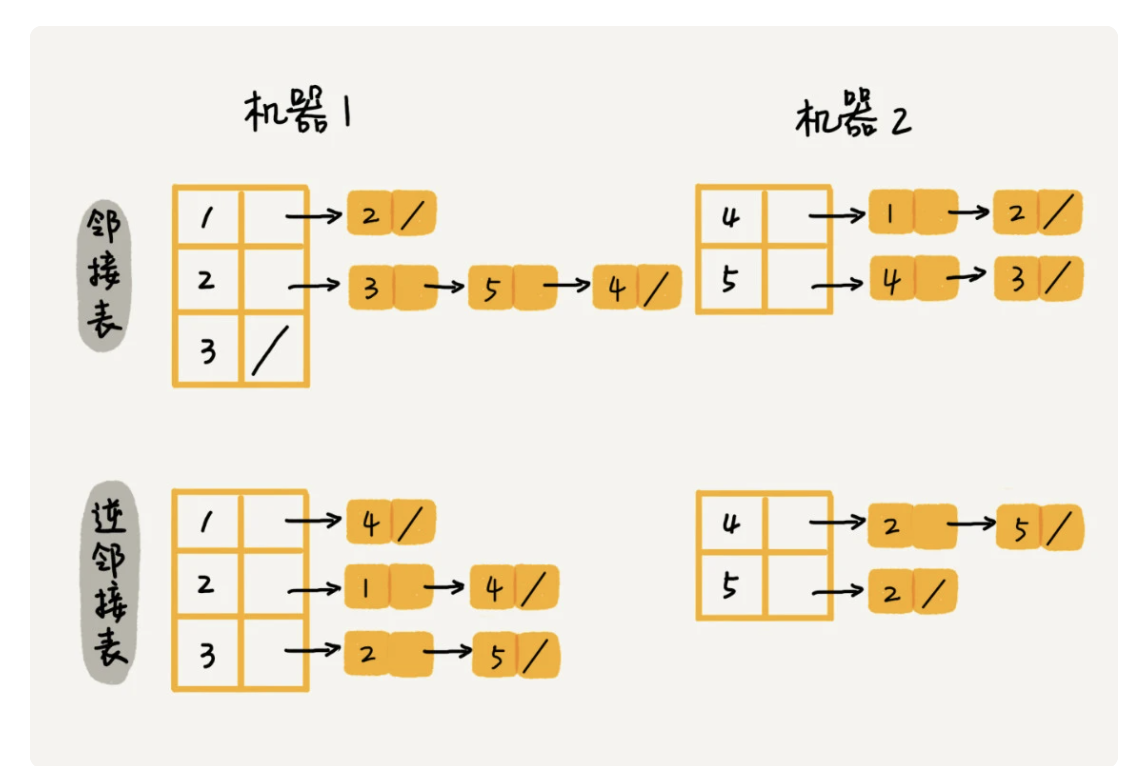
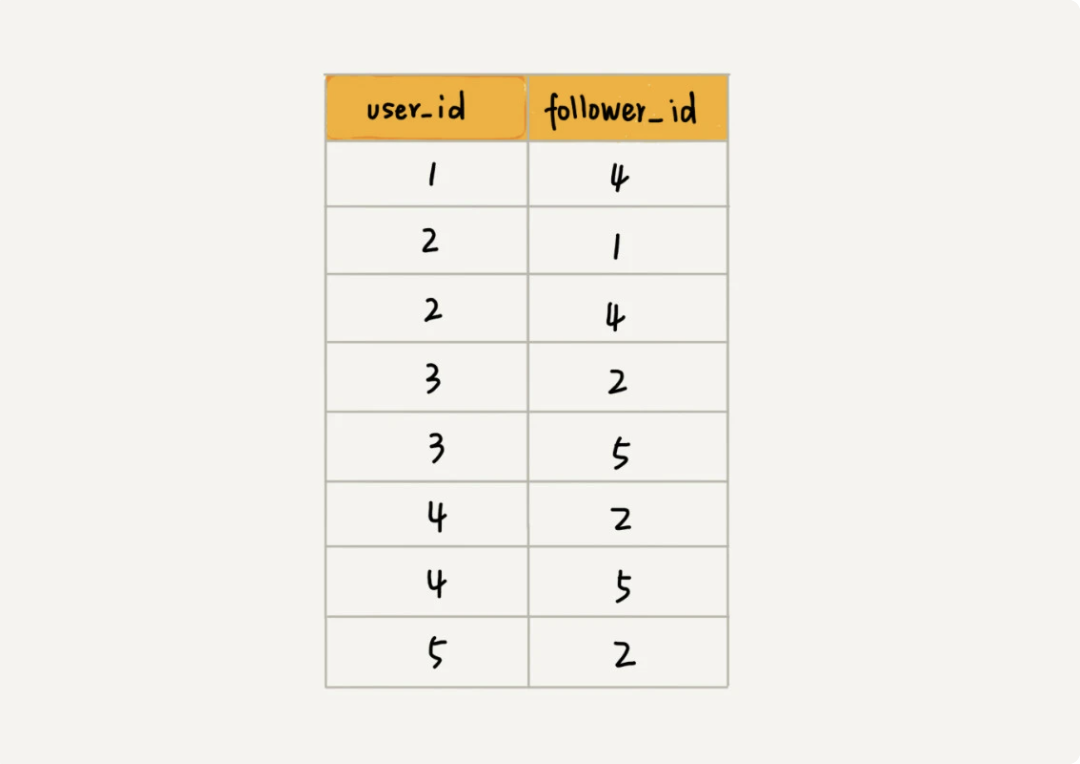
2.4、关系数据库存储顶点关系

 

 

 

三、图的遍历和搜索

3.1、广度优先搜素-邻接表

3.1.1代码

public class BFS {
    /**
     * 图的顶点个数
     */
    private int v;
    /**
     * 临接表的数组
     */
    private Grap[] adj;

    /**
     * 遍历
     *
     * @param s 出发的顶点
     * @param t 目标顶点
     */
    public void bfs(int s, int t) {
        if (s == t) {
            return;
        }
        //记录节点被访问过标记，防止重复访问
        boolean[] visited = new boolean[v];
        visited[s] = true;

        //基于队列缓存第K+1层节点
        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);

        //记录访问顶点的上一个顶点
        int[] prev = new int[v];
        for (int i = 0; i < v; ++i) {
            prev[i] = -1;
        }

        while (queue.size() != 0) {
            int w = queue.poll();
            for (int i = 0; i < adj[w].size(); ++i) {
                int q = adj[w].get(i);
                if (!visited[q]) {
                    prev[q] = w;
                    if (q == t) {
                        print(prev, s, t);
                        return;
                    }
                    visited[q] = true;
                    queue.add(q);
                }
            }
        }
    }

    private void print(int[] prev, int s, int t) { // 递归打印s->t的路径
        if (prev[t] != -1 && t != s) {
            print(prev, s, prev[t]);
        }
        System.out.print(t + " ");
    }
}


/**
 * 邻接表
 */
class Grap {
    /**
     * 顶点
     */
    int v;
    /**
     * 对应的邻接表
     */
    LinkedList<Integer> linkTable;

    /**
     * 图中顶点-连接的顶点个数大小
     *
     * @return
     */
    public Integer size() {
        return linkTable.size();
    }

    /**
     * 图中的顶点-获取邻接表的顶点
     *
     * @param i
     * @return
     */
    public Integer get(int i) {
        return linkTable.get(i);
    }
}

顶点 t 离起始顶点 s 很远，需要遍历完整个图才能找到。这个时候，每个顶点都要进出一遍队列，每个边也都会被访问一次，所以，广度优先搜索的时间复杂度是 O(V+E)，其中，V 表示顶点的个数，E 表示边的个数。当然，对于一个连通图来说，也就是说一个图中的所有顶点都是连通的，E 肯定要大于等于 V-1，所以，广度优先搜索的时间复杂度也可以简写为 O(E)。广度优先搜索的空间消耗主要在几个辅助变量 visited 数组、queue 队列、prev 数组上。这三个存储空间的大小都不会超过顶点的个数，所以空间复杂度是 O(V)。

3.1.2、搜索S到T的最短路径

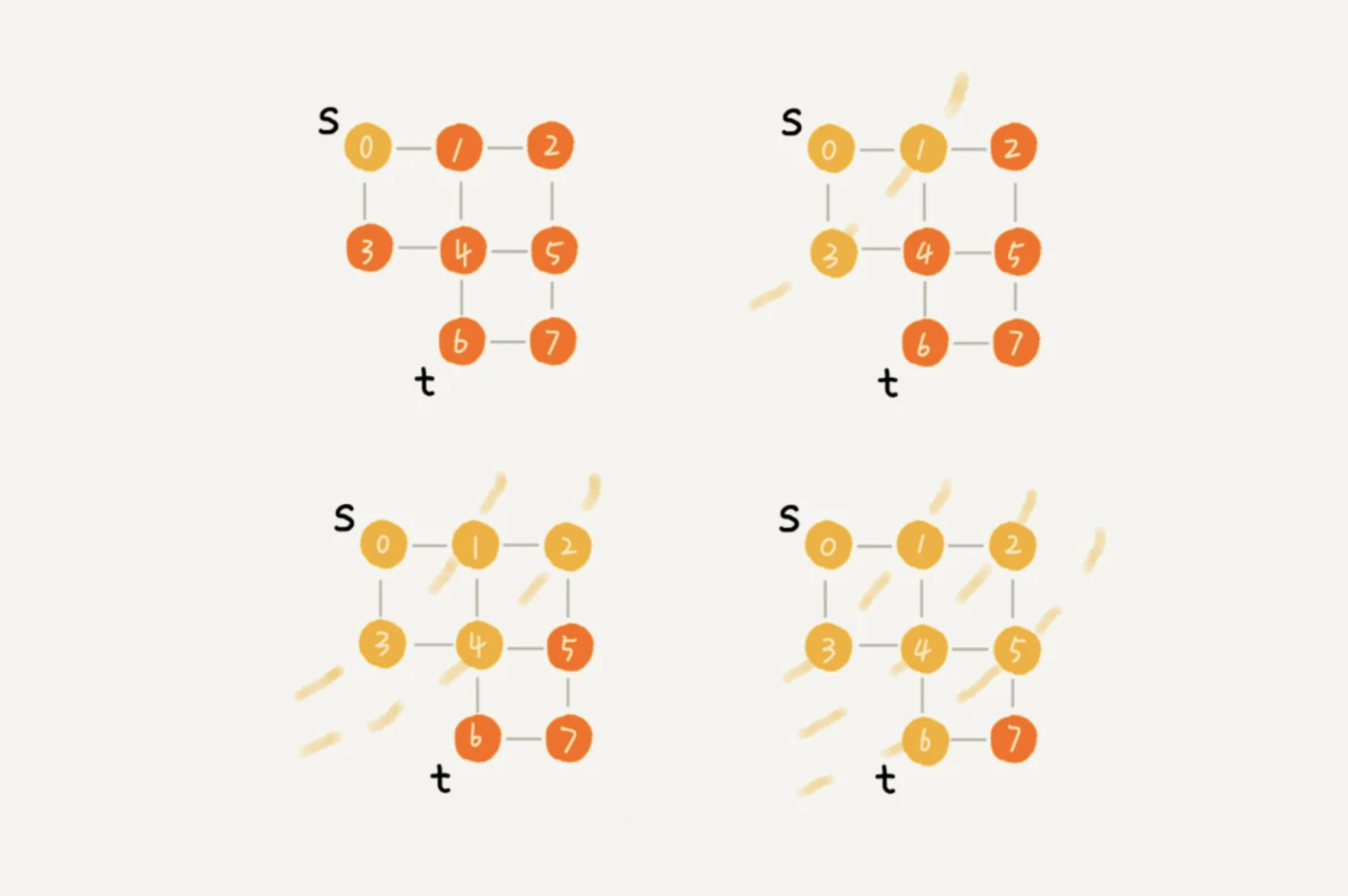
3.1.3、搜索步骤的分解图

 

 

 

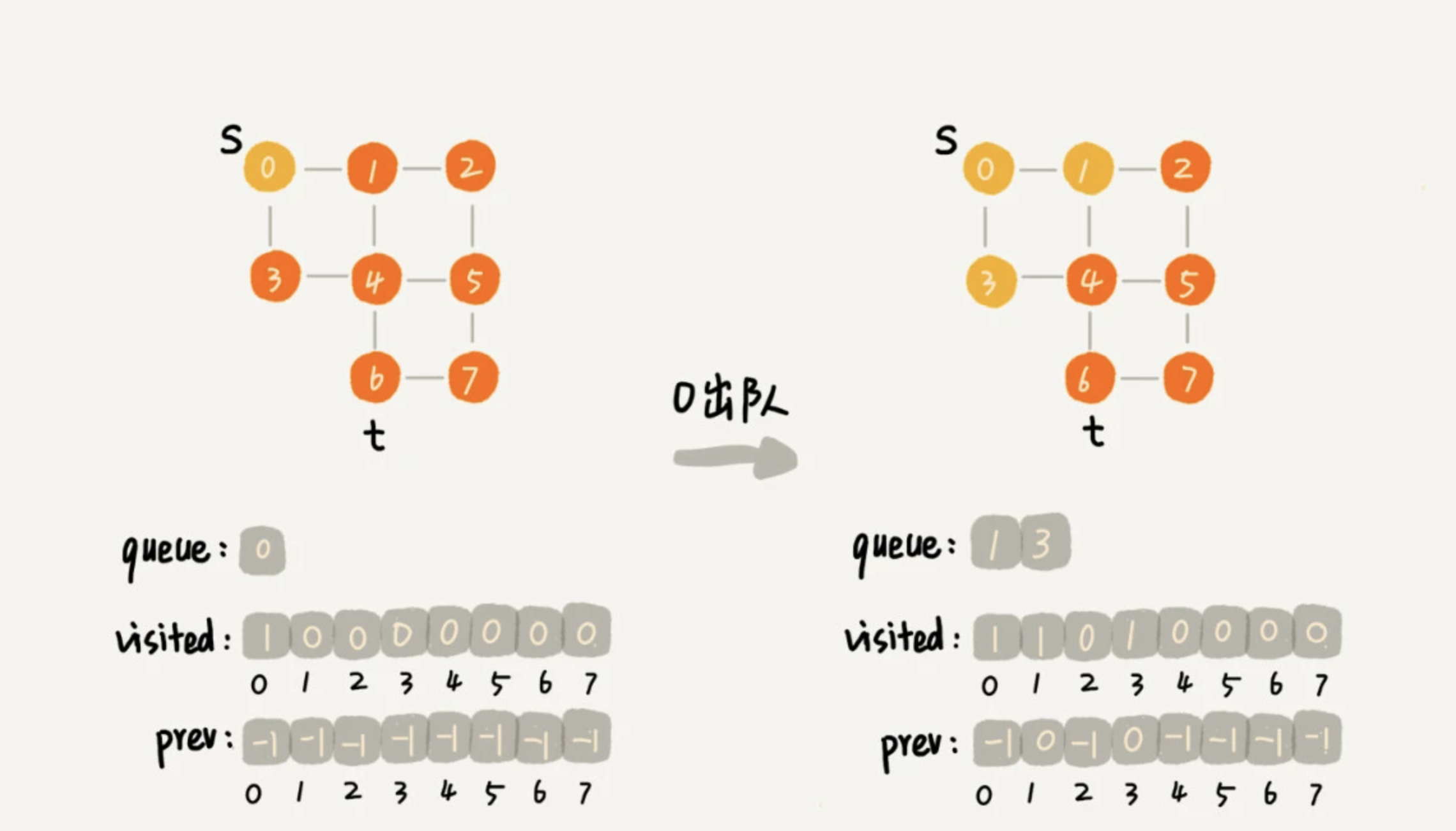
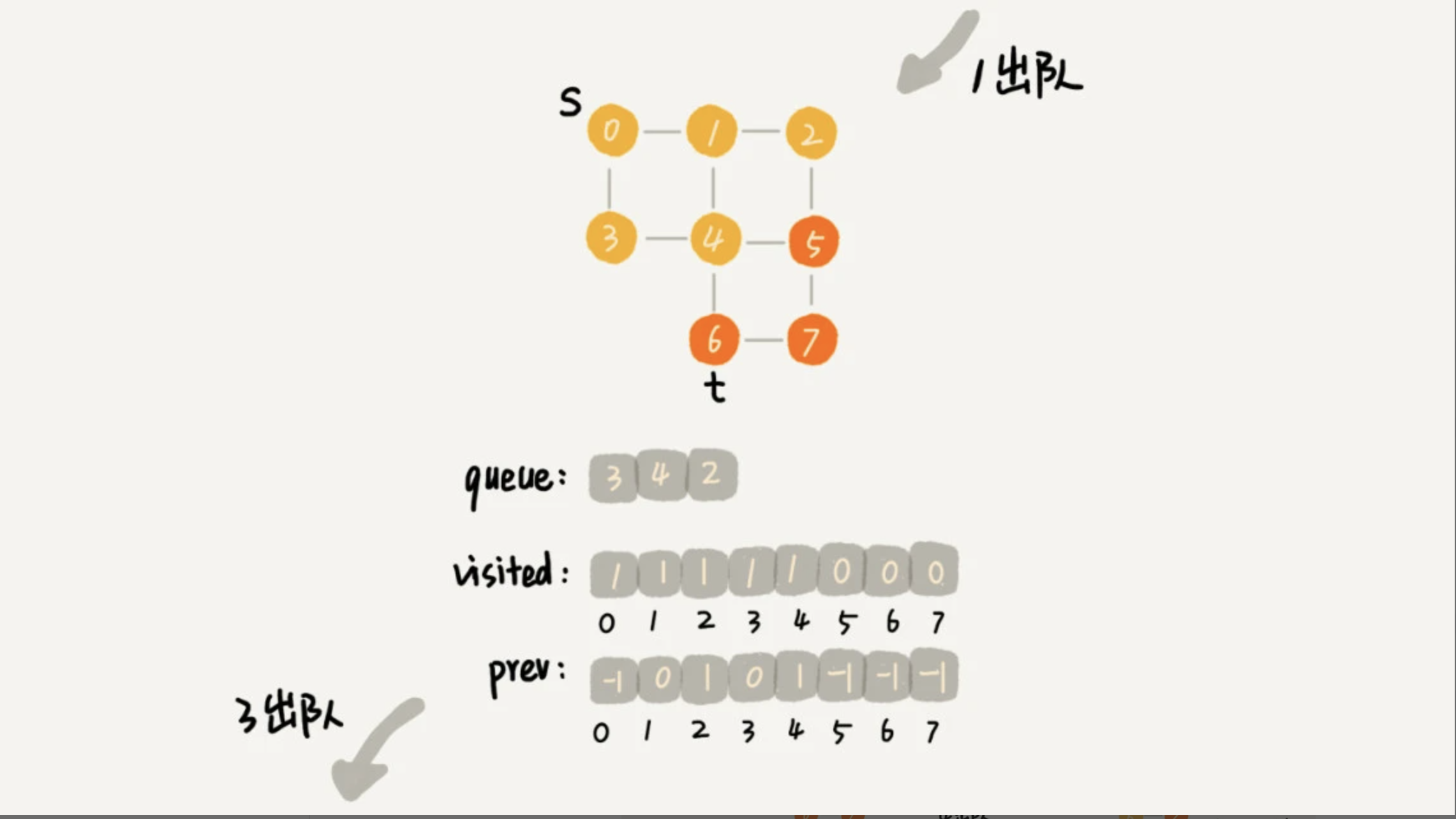
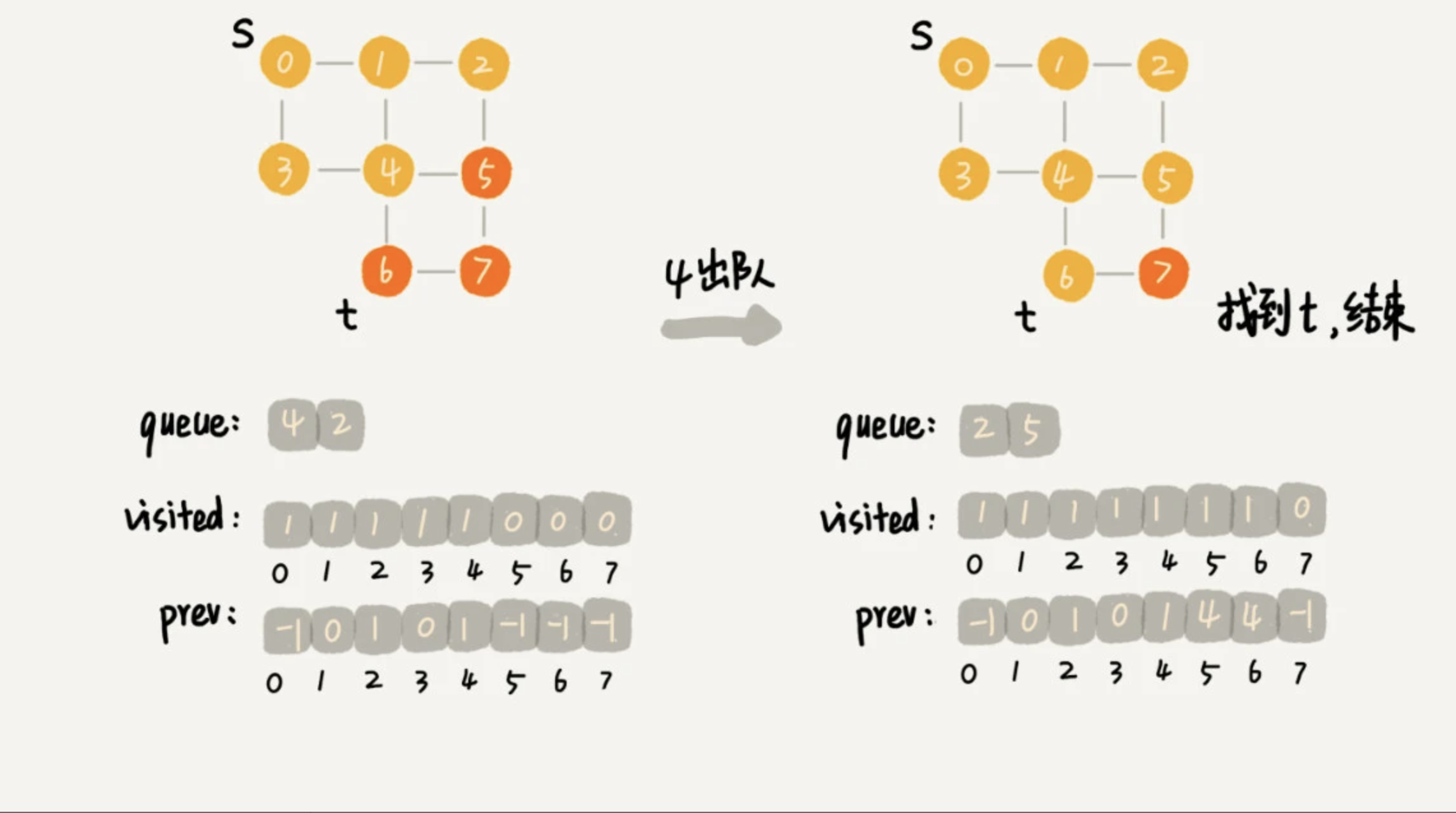
3.2、深度优先搜素-邻接表

3.2.1、代码

public class DFS {

    /**
     * 图的顶点个数
     */
    private int v;
    /**
     * 临接表的数组
     */
    private DFS.Grahp[] adj;

    boolean found = false; // 全局变量或者类成员变量


    public void dfs(int s, int t) {
        found = false;
        boolean[] visited = new boolean[v];
        int[] prev = new int[v];
        for (int i = 0; i < v; ++i) {
            prev[i] = -1;
        }
        recurDfs(s, t, visited, prev);
        print(prev, s, t);
    }


    private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
        if (found == true) {
            return;
        }
        visited[w] = true;
        if (w == t) {
            found = true;
            return;
        }
        for (int i = 0; i < adj[w].size(); ++i) {
            int q = adj[w].get(i);
            if (!visited[q]) {
                prev[q] = w;
                recurDfs(q, t, visited, prev);
            }
        }
    }

    private void print(int[] prev, int s, int t) { // 递归打印s->t的路径
        if (prev[t] != -1 && t != s) {
            print(prev, s, prev[t]);
        }
        System.out.print(t + " ");
    }

    public static class Grahp {
        /**
         * 顶点
         */
        int v;
        /**
         * 对应的邻接表
         */
        LinkedList<Integer> linkTable;

        /**
         * 图中顶点-连接的顶点个数大小
         *
         * @return
         */
        public Integer size() {
            return linkTable.size();
        }

        /**
         * 图中的顶点-获取邻接表的顶点
         *
         * @param i
         * @return
         */
        public Integer get(int i) {
            return linkTable.get(i);
        }
    }
}

3.2.2、搜索路径

深度优先搜索用的是一种比较著名的算法思想，回溯思想。这种思想解决问题的过程，非常适合用递归来实现。

从下面画的图可以看出，每条边最多会被访问两次，一次是遍历，一次是回退。所以，图上的深度优先搜索算法的时间复杂度是 O(E)，E 表示边的个数。深度优先搜索算法的消耗内存主要是 visited、prev 数组和递归调用栈。visited、prev 数组的大小跟顶点的个数 V 成正比，递归调用栈的最大深度不会超过顶点的个数，所以总的空间复杂度就是 O(V)。

 

 

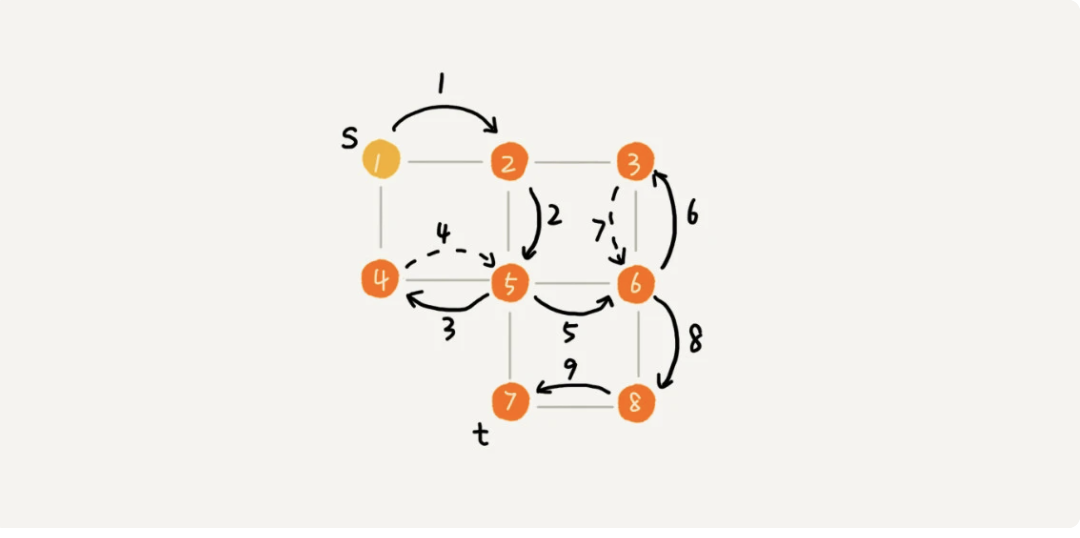
3.3、深度和广度优先搜索算法总结

广度优先搜索和深度优先搜索是图上的两种最常用、最基本的搜索算法，比起其他高级的搜索算法，比如 A*、IDA* 等，要简单粗暴，没有什么优化，所以，也被叫作暴力搜索算法。所以，这两种搜索算法仅适用于状态空间不大，也就是说图不大的搜索。

广度优先搜索，通俗的理解就是，地毯式层层推进，从起始顶点开始，依次往外遍历。

广度优先搜索需要借助队列来实现，遍历得到的路径就是，起始顶点到终止顶点的最短路径。

深度优先搜索用的是回溯思想，非常适合用递归实现。换种说法，深度优先搜索是借助栈来实现的。

在执行效率方面，深度优先和广度优先搜索的时间复杂度都是 O(E)，空间复杂度是 O(V)。