【数据结构和算法】排序之线性排序-桶排序,计数排序,基数排序
一、线性排序概念
三种时间复杂度是 O(n) 的排序算法:桶排序、计数排序、基数排序。
排序算法的时间复杂度是线性的,所以我们把这类排序算法叫作线性排序(Linear sort)。
能做到线性的时间复杂度,主要原因是,这三个算法是非基于比较的排序算法,都不涉及元素之间的比较操作。
桶排序,计数排序,基数排序的数据要求:
- 桶排序和计数排序的排序思想是非常相似的,都是针对范围不大的数据,将数据划分成不同的桶来实现排序。
- 基数排序要求数据可以划分成高低位,位之间有递进关系。比较两个数,我们只需要比较高位,高位相同的再比较低位。而且每一位的数据范围不能太大,因为基数排序算法需要借助桶排序或者计数排序来完成每一个位的排序工作。
二、桶排序
1、桶排序示意
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。

桶排序的时间复杂度为什么是 O(n) 呢?我们一块儿来分析一下。如果要排序的数据有 n 个,我们把它们均匀地划分到 m 个桶内,每个桶里就有 k=n/m 个元素。
每个桶内部使用快速排序,时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk),因为 k=n/m,所以整个桶排序的时间复杂度就是 O(n*log(n/m))。
当桶的个数 m 接近数据个数 n 时,log(n/m) 就是一个非常小的常量,这个时候桶排序的时间复杂度接近 O(n)。
2、适用桶排序的条件
- 要排序的数据需要很容易就能划分成 m 个桶
- 桶与桶之间有着天然的大小顺序
- 每个桶内的数据都排序完之后,桶与桶之间的数据不需要再进行排序
- 数据在各个桶之间的分布是比较均匀的
- (有些桶里的数据非常多,有些非常少,很不平均,那桶内数据排序的时间复杂度就不是常量级了。在极端情况下,如果数据都被划分到一个桶里,那就退化为 O(nlogn) 的排序算法了。)
3、桶排序的案例
比如说我们有 10GB 的订单数据,我们希望按订单金额(假设金额都是正整数)进行排序,但是我们的内存有限,只有几百 MB,没办法一次性把 10GB 的数据都加载到内存中.
答案:
(1)扫描文件,找出最小金额,最大金额
(2)将金额划分为多个桶(文件)
(3)如果数据分布不均匀,继续对不均匀的数据,划分多个桶(桶中的数据使用快排,桶中数据必须是内存能承受的住)。
(4)所有桶排序好后,然后根据桶的顺序,将各个桶中的数据,写入到一个大文件中,完成排序。
4、桶排序的一个伪代码
假设有30个数,机器一次排序,只能处理10个数,完成排序。
分3个桶,每个桶装10个数据,对每个桶进行快排,再合并3个桶的数据

public class BucketSort { /** * 每个桶容量的大小(可以想像一次数据排序,机器允许处理的最大条数) */ public static final int oneBucketMaxCount = 10; public static void main(String[] args) { int[] array = new int[]{30, 20, 10, 3, 2, 1, 13, 12, 11, 23, 22, 21, 24, 25, 26, 14, 15, 16, 4, 5, 6, 29, 28, 27, 9, 8, 7, 19, 18, 17}; System.out.println("排序前:" + Arrays.toString(array)); array = bucketSort(array); System.out.println("排序后:" + Arrays.toString(array)); } /** * 要排序的大数组 * * @param array */ public static int[] bucketSort(int[] array) { //===========step1:分桶================= //总数据量 int count = array.length; //每个桶的数据量(一次排序的内存最多允许的数据数量) int bucketMaxCount = oneBucketMaxCount; //根据总数据量求出分桶数据量( 总数据量/每个桶的上限值) int bucketCount = count / bucketMaxCount; //计算出一个桶索引的配置:key是分桶的key value是往该桶中放入数据的入口 Map<String, Bucket> map = new HashMap<>(); for (int i = 0; i < bucketCount; i++) { String key = buildBucketKey(i); map.put(key, new Bucket()); } //循环遍历往桶中放入对应桶的数据 for (int i = 0; i < array.length; i++) { //输入数据找到对应的桶key String bucketKey = mapBucketKey(array[i], bucketCount); //获取桶并放入数据 map.get(bucketKey).addElement(array[i]); } //===========step3:每个桶逐步排序=========== for (Map.Entry<String, Bucket> entry : map.entrySet()) { Bucket bucket = entry.getValue(); //获取所有数据,并进行排序 quickSort(bucket.getAllData()); } //===========step4:合并桶分桶成1个大桶完成排序===== //假设总数是这30个 Bucket allData = new Bucket(30); for (Map.Entry<String, Bucket> entry : map.entrySet()) { for (int data : entry.getValue().getAllData()) { allData.addElement(data); } } return allData.getAllData(); } /** * 根据通号生成桶key * * @param bucketIndex * @return */ private static String buildBucketKey(int bucketIndex) { return String.valueOf(bucketIndex); } /** * 根据数据生成桶key * * @param data * @return */ private static String mapBucketKey(int data, int bucketCount) { if (data >= 1 && data <= 10) { return String.valueOf(0); } else if (data > 10 && data <= 20) { return String.valueOf(1); } else if (data > 20 && data <= 30) { return String.valueOf(2); } return "-1"; } /** * 桶 */ public static class Bucket { //加入每个桶有10个数 private int[] datas = new int[10]; private int index = 0; public Bucket() { } public Bucket(int dataLength) { datas = new int[dataLength]; } //向桶中加入数据 public void addElement(int data) { datas[index++] = data; } //假设获取到该桶中的所有数据 public int[] getAllData() { return datas; } } //================快排的代码 start==================== private static int[] quickSort(int[] array) { if (array == null || array.length <= 1) { return array; } //快速排序 quickSort(array, 0, array.length - 1); return array; } private static void quickSort(int[] array, int leftIndex, int rightIndex) { if (leftIndex >= rightIndex) { return; } //对数组进行分区 int partitionIndex = partition(array, leftIndex, rightIndex); //排序左边数组 quickSort(array, leftIndex, partitionIndex - 1); //排序右边数组 quickSort(array, partitionIndex + 1, rightIndex); } private static int partition(int[] array, int leftIndex, int rightIndex) { //用数组的最右边的元素作为分区元素 int target = array[rightIndex]; //声明一个分区的下标元素(作为左侧扫描下标) int i = leftIndex; int tmp; for (int j = leftIndex; j < rightIndex; j++) { if (array[j] < target) { tmp = array[j]; array[j] = array[i]; array[i] = tmp; //左边指针向右移动1位 i++; } } tmp = array[rightIndex]; array[rightIndex] = array[i]; array[i] = tmp; return i; } //================快排的代码 end==================== }
测试结果:
排序前:[30, 20, 10, 3, 2, 1, 13, 12, 11, 23, 22, 21, 24, 25, 26, 14, 15, 16, 4, 5, 6, 29, 28, 27, 9, 8, 7, 19, 18, 17]
排序后:[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]
三、计数排序
我个人觉得,计数排序其实是桶排序的一种特殊情况。当要排序的n个数据,所处的范围并不大的时候,比如最大值是k,我们就可以把数据划分成k个桶。每个桶内的数据值都是相同的,省掉了桶内排序的时间。
我们都经历过高考,高考查分数系统你还记得吗?我们查分数的时候,系统会显示我们的成绩以及所在省的排名。如果你所在的省有50万考生,如何通过成绩快速排序得出名次呢?
考生的满分是900分,最小是0分,这个数据的范围很小,所以我们可以分成901个桶,对应分数从0分到900分。根据考生的成绩,我们将这50万考生划分到这901个桶里。桶内的数据都是分数相同的考生,所以并不需要再进行排序。我们只需要依次扫描每个桶,将桶内的考生依次输出到一个数组中,就实现了50万考生的排序。因为只涉及扫描遍历操作,所以时间复杂度是O(n)。
想弄明白这个问题,我们就要来看计数排序算法的实现方法。我还拿考生那个例子来解释。为了方便说明,我对数据规模做了简化。假设只有8个考生,分数在0到5分之间。这8个考生的成绩我们放在一个数组A[8]中,它们分别是:2,5,3,0,2,3,0,3。
考生的成绩从0到5分,我们使用大小为6的数组C[6]表示桶,其中下标对应分数。不过,C[6]内存储的并不是考生,而是对应的考生个数。像我刚刚举的那个例子,我们只需要遍历一遍考生分数,就可以得到C[6]的值。
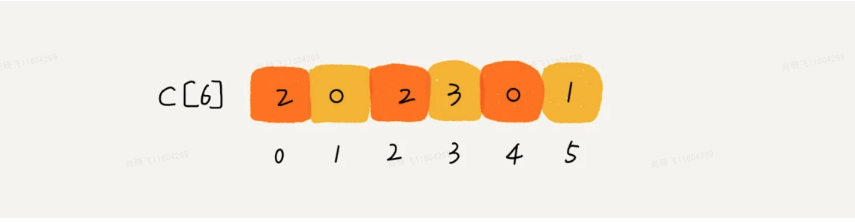
【图A】
从图中可以看出,分数为3分的考生有3个,小于3分的考生有4个,所以,成绩为3分的考生在排序之后的有序数组R[8]中,会保存下标4,5,6的位置。
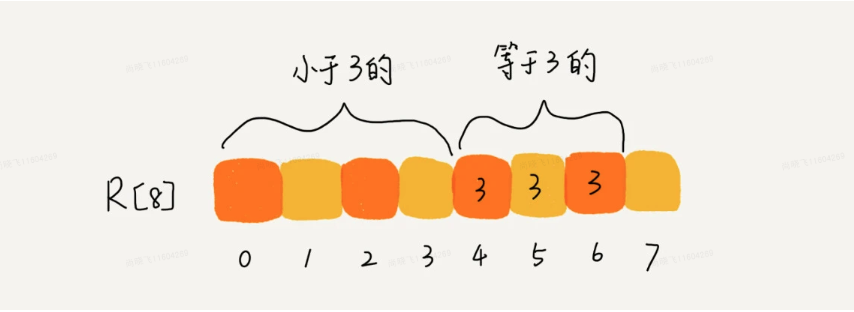
【图B】
那我们如何快速计算出,每个分数的考生在有序数组中对应的存储位置呢?这个处理方法非常巧妙,很不容易想到。
思路是这样的:我们对C[6]数组顺序求和,C[6]存储的数据就变成了下面这样子。C[k]里存储小于等于分数k的考生个数。
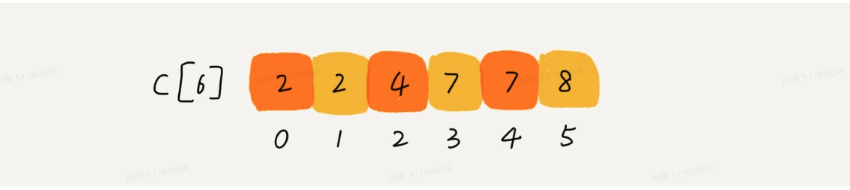
【图C】
对【图A】从第二个数开始遍历执行 C[i]=C[i]+C[i-1],就变成了【图C】, 这边遍历完之后,C[i]表示当前该数据i 在有序数组中有几个小于和等于i的数,同时也表示了自己应该放在有序数组中的下标。
有了前面的数据准备之后,现在我就要讲计数排序中最复杂、最难理解的一部分了,请集中精力跟着我的思路!
我们从后到前依次扫描数组A。比如,当扫描到3时,我们可以从数组C中取出下标为3的值7,也就是说,到目前为止,包括自己在内,分数小于等于3的考生有7个,也就是说3是数组R中的第7个元素(也就是数组R中下标为6的位置)。当3放入到数组R中后,小于等于3的元素就只剩下了6个了,所以相应的C[3]要减1,变成6。
以此类推,当我们扫描到第2个分数为3的考生的时候,就会把它放入数组R中的第6个元素的位置(也就是下标为5的位置)。当我们扫描完整个数组A后,数组R内的数据就是按照分数从小到大有序排列的了。
具体过程如下图:
1、计数排序的场景(桶排序的特殊情况)
对A[8]==>2,5,3,0,2,3,0,3。 进行计数排序。
计数排序中可以从头向后取数据吗?个人感觉似乎是一样的过程==>可以的 但就不是稳定排序算法了

2、计数排序使用场景
整体过程:
- step1:遍历【待排序原数组】,确认范围,并对数据进行桶计数,产出【桶计数数组】
- step2:遍历【桶计数数组】,对其内容执行C[i] = C[i] +C[i-1] , 产生排序的依据数据。
- step3:生成一个【有序空数组】,从后向前遍历扫描【待排序原数组】,结合【桶计数数组】,将数据有序放在【有序空数组】中,完成排序
计数排序只能用在数据范围不大的场景中,如果数据范围 k 比要排序的数据 n 大很多,就不适合用计数排序了。
计数排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数。

还是拿考生这个例子。如果考生成绩精确到小数后一位,我们就需要将所有的分数都先乘以 10,转化成整数,然后再放到 9010 个桶内。再比如,如果要排序的数据中有负数,数据的范围是[-1000, 1000],那我们就需要先对每个数据都加 1000,转化成非负整数。
3、计数排序的案例

// 计数排序,a是数组,n是数组大小。假设数组中存储的都是非负整数。 public void countingSort(int[] a, int n) { if (n <= 1) { return; } // 查找数组中数据的范围 int max = a[0]; for (int i = 1; i < n; ++i) { if (max < a[i]) { max = a[i]; } } int[] c = new int[max + 1]; // 申请一个计数数组c,下标大小[0,max] for (int i = 0; i <= max; ++i) { c[i] = 0; } // 计算每个元素的个数,放入c中 for (int i = 0; i < n; ++i) { c[a[i]]++; } // 依次累加 for (int i = 1; i <= max; ++i) { c[i] = c[i - 1] + c[i]; } // 临时数组r,存储排序之后的结果 int[] r = new int[n]; // 计算排序的关键步骤,有点难理解 for (int i = n - 1; i >= 0; --i) { int index = c[a[i]] - 1; r[index] = a[i]; c[a[i]]--; } // 将结果拷贝给a数组 for (int i = 0; i < n; ++i) { a[i] = r[i]; } }
四、基数排序
1、基数排序分解图
我用字符串排序的例子,画了一张基数排序的过程分解图,
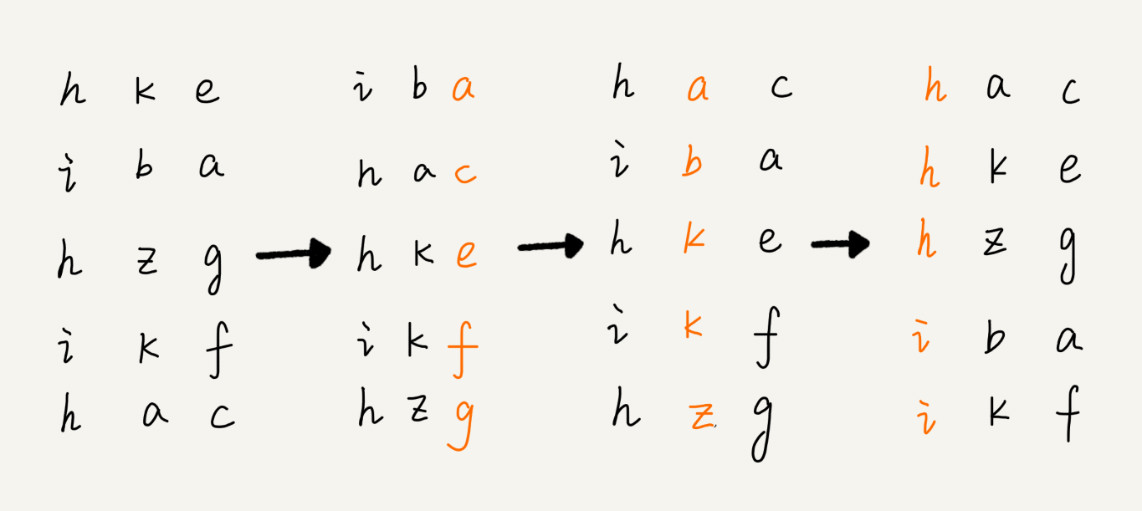
代码实现:

/** * 基数排序 **/ public class BaseDataSort { public static final Map<Character,Integer> charMap =new HashMap<>(); static { charMap.put(Character.valueOf('a'),0); charMap.put(Character.valueOf('b'),1); charMap.put(Character.valueOf('c'),2); charMap.put(Character.valueOf('d'),3); charMap.put(Character.valueOf('e'),4); charMap.put(Character.valueOf('f'),5); charMap.put(Character.valueOf('g'),6); charMap.put(Character.valueOf('h'),7); charMap.put(Character.valueOf('i'),8); charMap.put(Character.valueOf('j'),9); charMap.put(Character.valueOf('k'),10); charMap.put(Character.valueOf('l'),11); charMap.put(Character.valueOf('m'),12); charMap.put(Character.valueOf('n'),13); charMap.put(Character.valueOf('o'),14); charMap.put(Character.valueOf('p'),15); charMap.put(Character.valueOf('q'),16); charMap.put(Character.valueOf('r'),17); charMap.put(Character.valueOf('s'),18); charMap.put(Character.valueOf('t'),19); charMap.put(Character.valueOf('u'),20); charMap.put(Character.valueOf('v'),21); charMap.put(Character.valueOf('w'),22); charMap.put(Character.valueOf('x'),23); charMap.put(Character.valueOf('y'),24); charMap.put(Character.valueOf('z'),25); } public static void main(String[] args) { String[] array = new String[]{"hke","iba","hzg","ikf","hac"}; baseDataSort(array,2); } public static String[] baseDataSort(String[] array,int charIndex){ if(charIndex <0){ return array; } Bucket[] buckets = new Bucket[26]; //对最后一位进行排序 for(int i=0;i<array.length;i++){ String String = array[i]; int index = charMap.get(String.charAt(charIndex)); if(buckets[index] == null){ buckets[index] = new Bucket(); } buckets[index].addElement(array[i]); } String[] first= new String[array.length]; int j=0; for(int i=0;i<buckets.length;i++){ if(buckets[i]!=null){ String[] a= buckets[i].getAllData(); for(String e:a){ first[j]=e; j++; } } } System.out.println("第"+(3-charIndex)+"次的排序结果"+ Arrays.toString(first)); return baseDataSort(first,charIndex-1); } private static class Bucket{ private List<String> data = new ArrayList<>(); private char c; public void addElement(String e){ data.add(e); } public String[] getAllData(){ return data.toArray(new String[data.size()]); } } }
测试结果:
第1次的排序结果[iba, hac, hke, ikf, hzg]
第2次的排序结果[hac, iba, hke, ikf, hzg]
第3次的排序结果[hac, hke, hzg, iba, ikf]
2、基数排序的场景
- 基数排序对要排序的数据是有要求的,需要可以分割出独立的“位”来比较,而且位之间有递进的关系。
- 如果 a 数据的高位比 b 数据大,那剩下的低位就不用比较了
- 每一位的数据范围不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到 O(n) 了。
3、基数排序的案例
1.算法原理(以排序10万个手机号为例来说明)
1)比较两个手机号码a,b的大小,如果在前面几位中a已经比b大了,那后面几位就不用看了。
2)借助稳定排序算法的思想,可以先按照最后一位来排序手机号码,然后再按照倒数第二位来重新排序,以此类推,最后按照第一个位重新排序。
3)经过11次排序后,手机号码就变为有序的了。
4)每次排序有序数据范围较小,可以使用桶排序或计数排序来完成。



