【数据结构和算法】排序之归并排序，快速排序

分治思想跟我们前面讲的递归思想很像。是的，分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧

一、归并排序

1、归并排序的原理

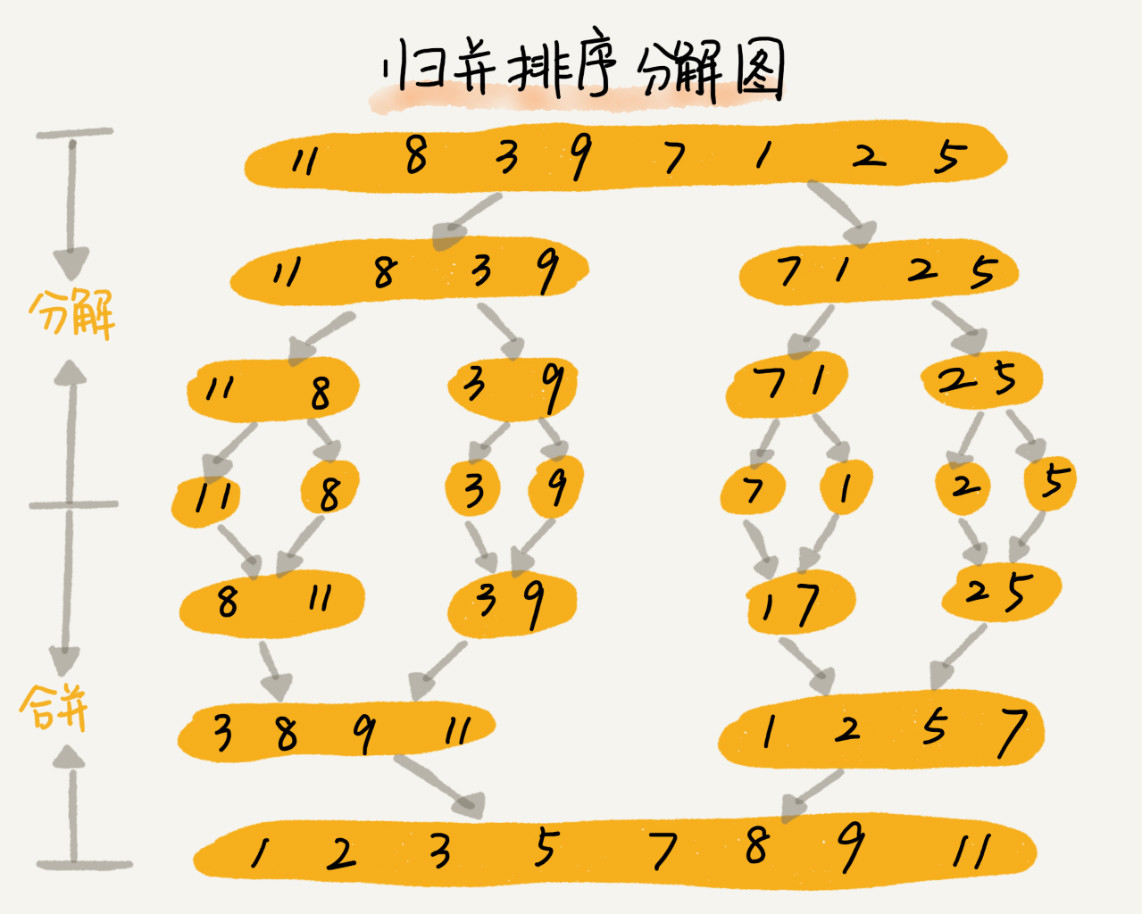
2、归并排序的分析

• 是否是稳定排序：在合并数组的环节，当左右数组的元素相同时，优先放左侧元素到合并数组中，则为稳定排序算法。
• 空间复杂度：O(n),在merge阶段需要申请临时数组进行合并，故不是原地排序算法
• 时间复杂度：T(n)=O(nlogn)

3、归并排序的案例

（1）递推公式

递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))

终止条件：
p >= r 不用再继续分解

（2）案例：

https://www.cnblogs.com/shangxiaofei/articles/10890150.html

 

二、快速排序

1、快速排序的原理

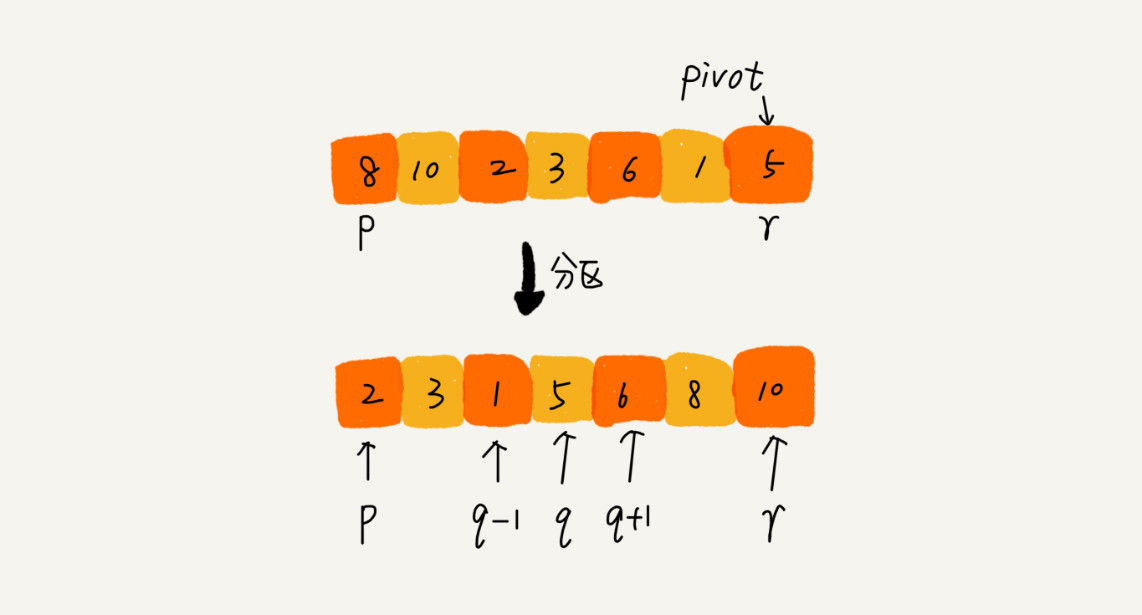
快排的思想是这样的：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

2、快速排序的分析

空间复杂度：原地排序，O(1)

是否为稳定排序算法：不是稳定的排序算法，寻找分区的时候,会对数据进行交换导致相同值顺序变化。

时间复杂度

• 平均时间复杂度：O(n*lgn) (取决于分区数据的选择，是否会将数组拆成对等的左，右两部分)
• 时间复杂度会退化为O(n^2):我举一个比较极端的例子。如果数组中的数据原来已经是有序的了，比如 1，3，5，6，8。如果我们每次选择最后一个元素作为 pivot，那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素，这种情况下，快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。

 

3、快速排序的案例

（1）递推公式

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)

终止条件：
p >= r

（2）代码案例

 /**
     * 快速排序
     *
     * @param array
     * @return
     */
    public static int[] quickSort(int[] array) {
        if (array == null || array.length <= 1) {
            return array;
        }
        //快速排序
        quickSort(array, 0, array.length - 1);
        return array;
    }

    private static void quickSort(int[] array, int leftIndex, int rightIndex) {
        if (leftIndex >= rightIndex) {
            return;
        }
        //对数组进行分区
        int partitionIndex = partition(array, leftIndex, rightIndex);
        //排序左边数组
        quickSort(array, leftIndex, partitionIndex - 1);
        //排序右边数组
        quickSort(array, partitionIndex + 1, rightIndex);
    }


    private static int partition(int[] array, int leftIndex, int rightIndex) {
        //用数组的最右边的元素作为分区元素
        int target = array[rightIndex];
        //声明一个分区的下标元素(作为左侧扫描下标)
        int i = leftIndex;
        int tmp;

        for (int j = leftIndex; j < rightIndex; j++) {
            if (array[j] < target) {
                tmp = array[j];
                array[j] = array[i];
                array[i]=tmp;
                //左边指针向右移动1位
                i++;
            }
        }

        tmp = array[rightIndex];
        array[rightIndex] = array[i];
        array[i]=tmp;

        return i;
    }

 

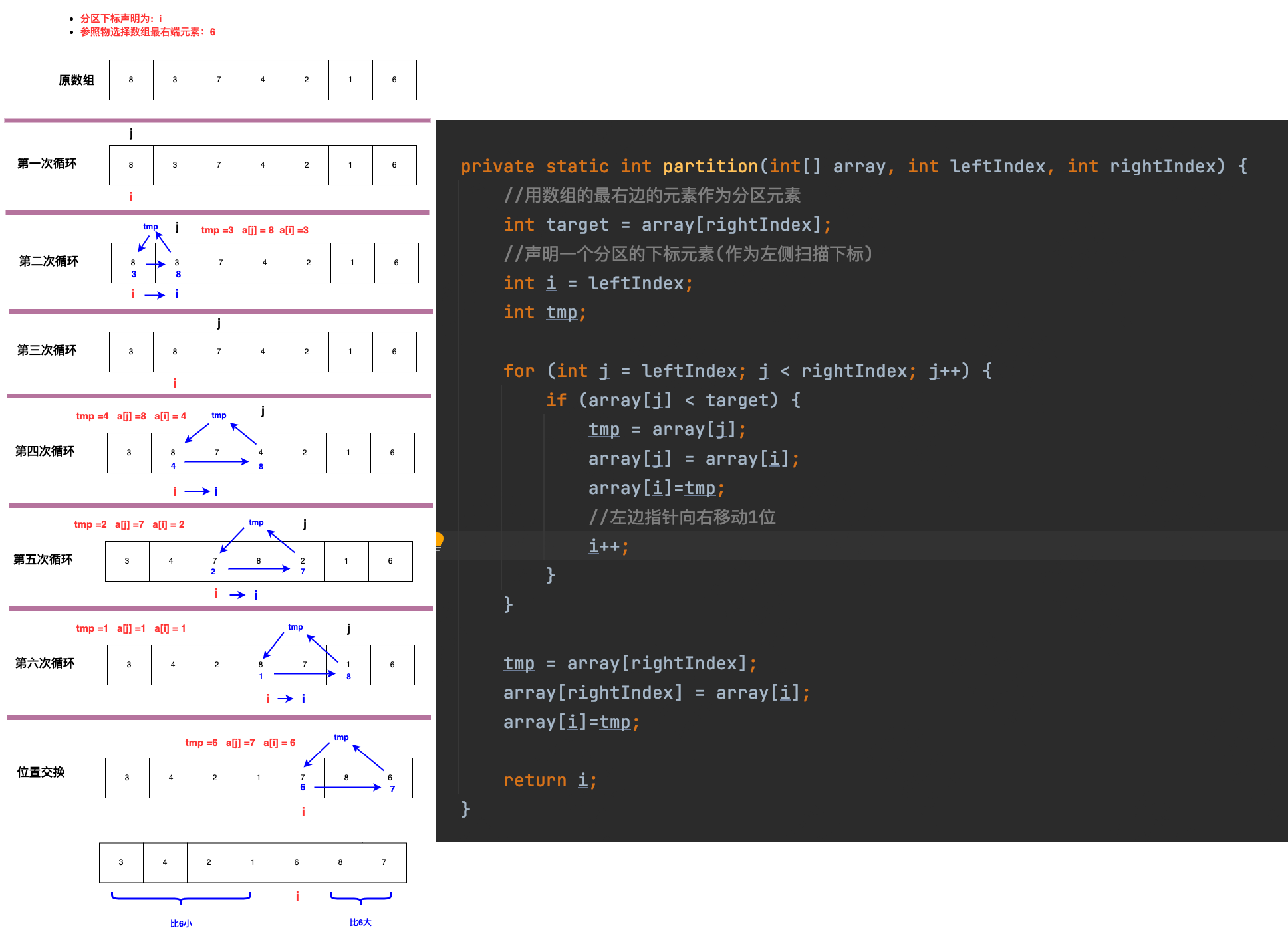
https://www.cnblogs.com/shangxiaofei/articles/10978864.html

 

 

快速排序和归并排序的区别

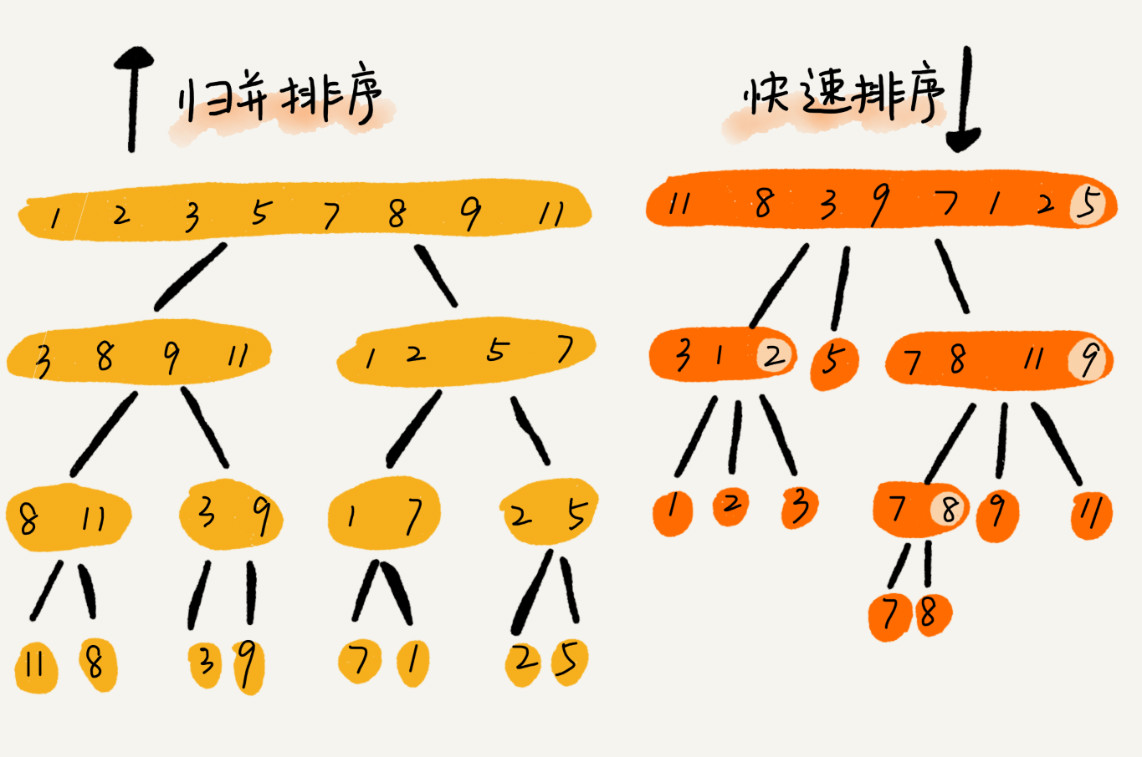
可以发现，归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。我们前面讲过，归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。

 

 

算法题：如何用快排思想在O(n)内查找第K大元素？

快排核心思想就是分治和分区，我们可以利用分区的思想，来解答开篇的问题：O(n) 时间复杂度内求无序数组中的第 K 大元素。比如，[6,1,3,5,7,2,4,9,11,8]这样一组数据，第 3 大元素就是 8。

我们选择数组区间 A[0…n-1]的最后一个元素 A[n-1]作为 pivot，对数组 A[0…n-1]原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。

• 如果 p+1=K，那 A[p]就是要求解的元素；
• 如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1]区间，我们再按照上面的思路递归地在 A[p+1…n-1]这个区间内查找。
• 如果 K<p+1，那我们就在 A[0…p-1]区间查找。

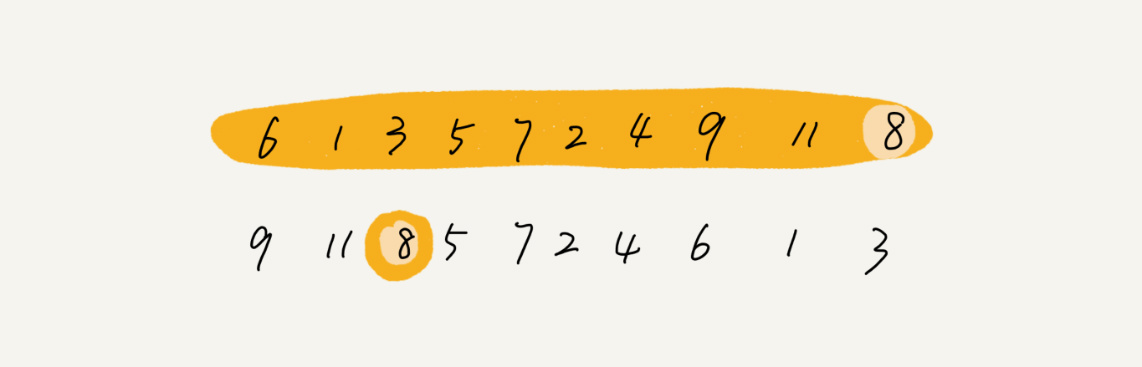
我们再来看，为什么上述解决思路的时间复杂度是 O(n)？

• 第一次分区查找，我们需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。
• 第二次分区查找，我们只需要对大小为 n/2 的数组执行分区操作，需要遍历 n/2 个元素。
• 依次类推，分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。
• 如果我们把每次分区遍历的元素个数加起来，就是：n+n/2+n/4+n/8+…+1。这是一个等比数列求和，最后的和等于 2n-1。所以，上述解决思路的时间复杂度就为 O(n)。

案例：

public static void main(String[] args) {

        int[] array = {10,1,2,3,4,8,8,11,0,1,2};
        int data = findKnData(array,0,array.length-1,3 );
        System.out.println(data);

    }


    public static int findKnData(int[] array, int left, int right, int kn) {
        if (array == null || kn <= 0 || array.length < kn) {
            //如果数组为空，或数组的长度小于Kn,则认为入参有问题
            throw new IllegalArgumentException();
        }
        int partitionIn = partitionIn(array, left, right);
        if (partitionIn + 1 == kn) {
            //则表名该元素为数组中第kn大元素
            return array[partitionIn];
        } else if (partitionIn + 1 > kn) {
            return findKnData(array, left, partitionIn - 1, kn);
        } else {
            return findKnData(array, partitionIn + 1, right, kn);
        }
    }


    private static int partitionIn(int[] array, int left, int right) {
        if (left == right) {
            return left;
        }

        int i = left;
        int tmp;
        int compareData = array[right];
        for (int j = left; j <= right - 1; j++) {
            //如果j位置的元素比比较元素大，则进行位置交换，交换至i的左边
            if (array[j] > compareData) {
                tmp = array[j];
                array[j] = array[i];
                array[i] = tmp;
                i++;
            }
        }
        //将比较的元素和i的位置进行交换
        tmp=array[i];
        array[i]=array[right];
        array[right]=tmp;
        return i;
    }

 

 

算法题：基于选择排序找第N大的元素

   //将数组分为有序 和 无序两部分。 
    public static int findMaxData2(int[] array,int sortIndex){
        if(array==null || array.length<sortIndex){
            return -1;
        }
        if(array.length==1&&sortIndex==1){
            return array[0];
        }

        int maxData=0;
        int maxIndex=-1;
        int tmp=0;
        //外层控制有序数组的增长
        for(int i=0;i<array.length;i++){
            maxData=array[i];
            maxIndex=i;

            //内层控制，在无序数组中找到最大元素，并扩大有序数组
            for(int j=i;j<array.length;j++){

                if(array[j]>maxData){
                    maxData=array[j];
                    maxIndex=j;
                }
            }
            
           //将从无序数组部分的最大元素加入到有序数据的末尾 
           tmp =array[i];
           array[i]=maxData;
           array[maxIndex] =tmp;
           
           //如果当前有序数组的长度等于了第N大元素的位置，则表示找到了第N大元素
           if(i==sortIndex-1){
               return array[i];
           }
        }
        return -1;
    }