【数据结构和算法】之排序算法-冒泡，插入，选择排序

算法过程动态图：https://visualgo.net/

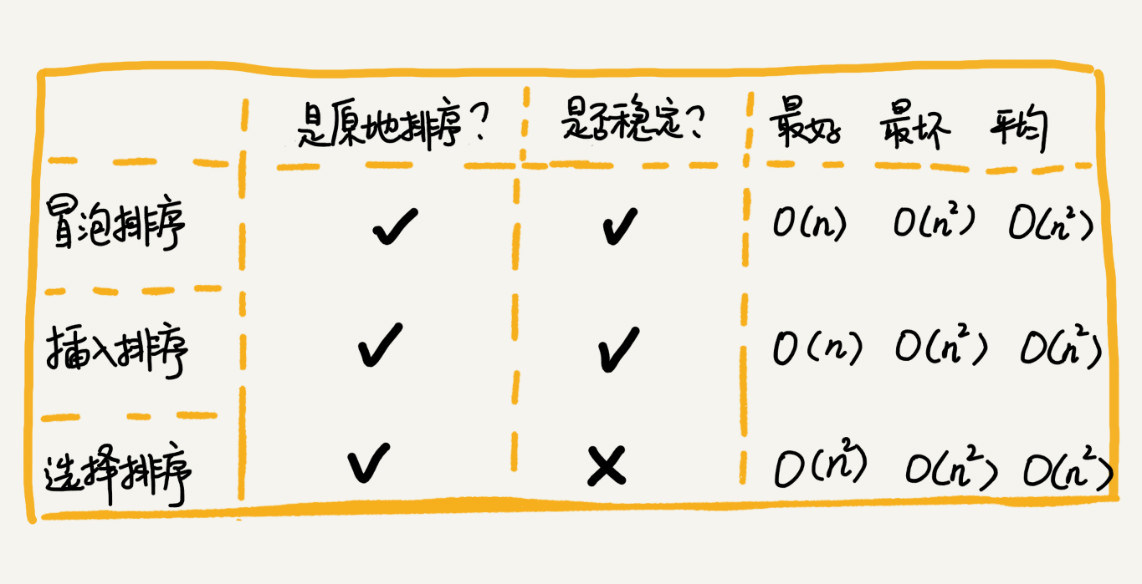
一、排序算法对比

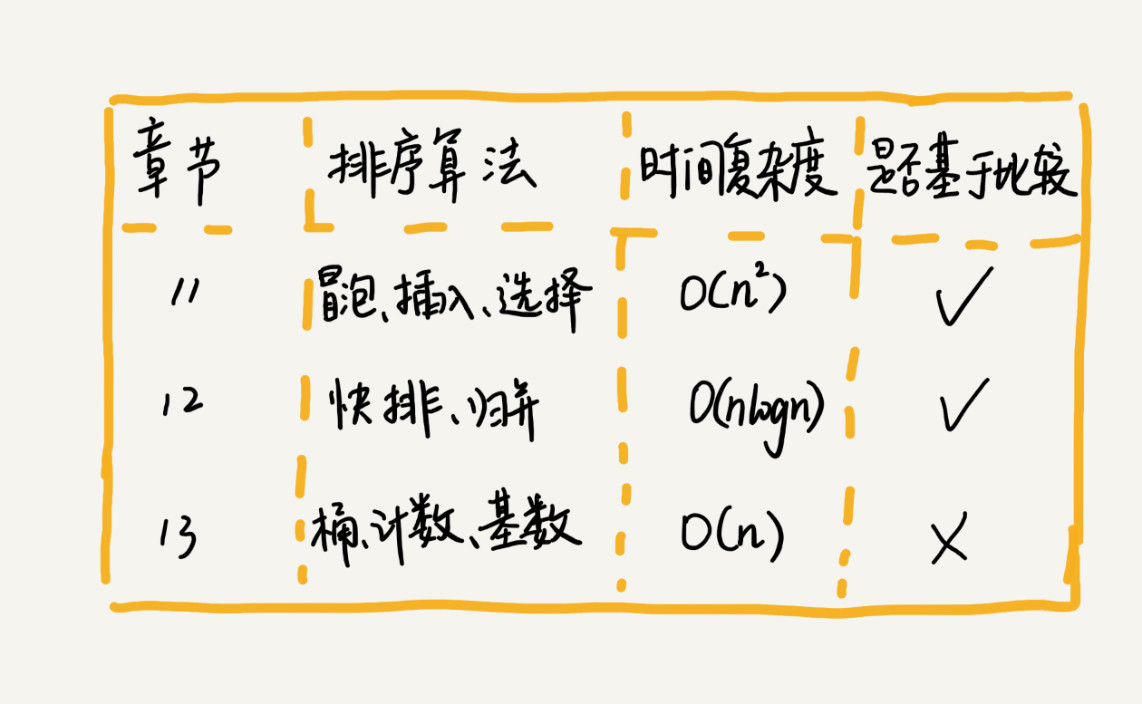
二、如何衡量排序算法

1、排序算法的执行效率

• 最好情况、最坏情况、平均情况时间复杂度。（依赖-数据的有序性）
• 时间复杂度的系数、常数 、低阶。（在同一级别数据量时，衡量，就需要把系统，常数，低阶数据考虑在内）
• 比较次数和交换（或移动）次数（排序过程中，数据交换的次数）

2、排序算法的内存消耗

• 算法的内存消耗可以通过空间复杂度来衡量，排序算法也不例外
• 原地排序（Sorted in place）。原地排序算法，就是特指空间复杂度是 O(1) 的排序算法

3、排序算法的稳定性

• 如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变，叫稳定的排序算法。否则叫不稳定的排序算法。
• 稳定排序算法，减少对象交换的次数。

 

排序算法稳定性的案例

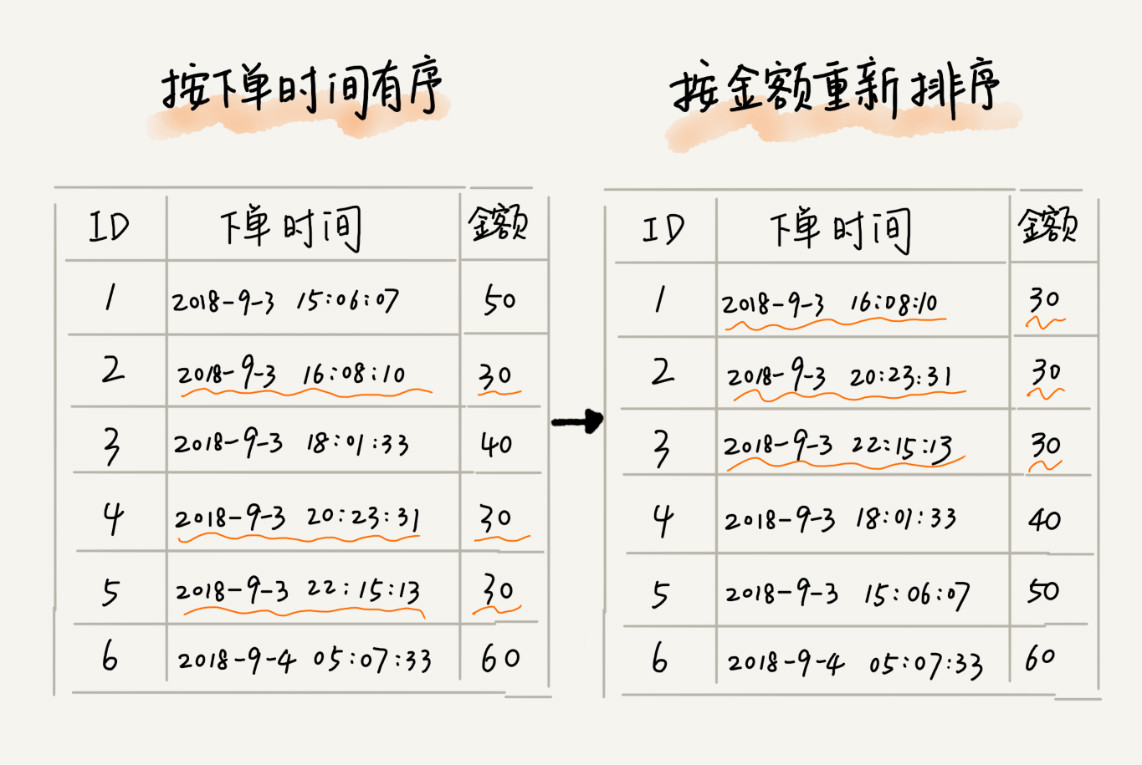
我们现在要给电商交易系统中的“订单”排序。订单有两个属性，一个是下单时间，另一个是订单金额。如果我们现在有 10 万条订单数据，我们希望按照金额从小到大对订单数据排序。对于金额相同的订单，我们希望按照下单时间从早到晚有序。

做法：

（1）先对订单时间进行排序，形成新的数组。

（2）使用稳定排序算法，对新数组使用稳定排序算法，按金额进行排序。

 

稳定排序算法可以保持金额相同的两个对象，在排序之后的前后顺序不变。第一次排序之后，所有的订单按照下单时间从早到晚有序了。在第二次排序中，我们用的是稳定的排序算法，所以经过第二次排序之后，相同金额的订单仍然保持下单时间从早到晚有序。

 

 

三、冒泡排序算法

1、第一次冒泡操作的过程

每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作。

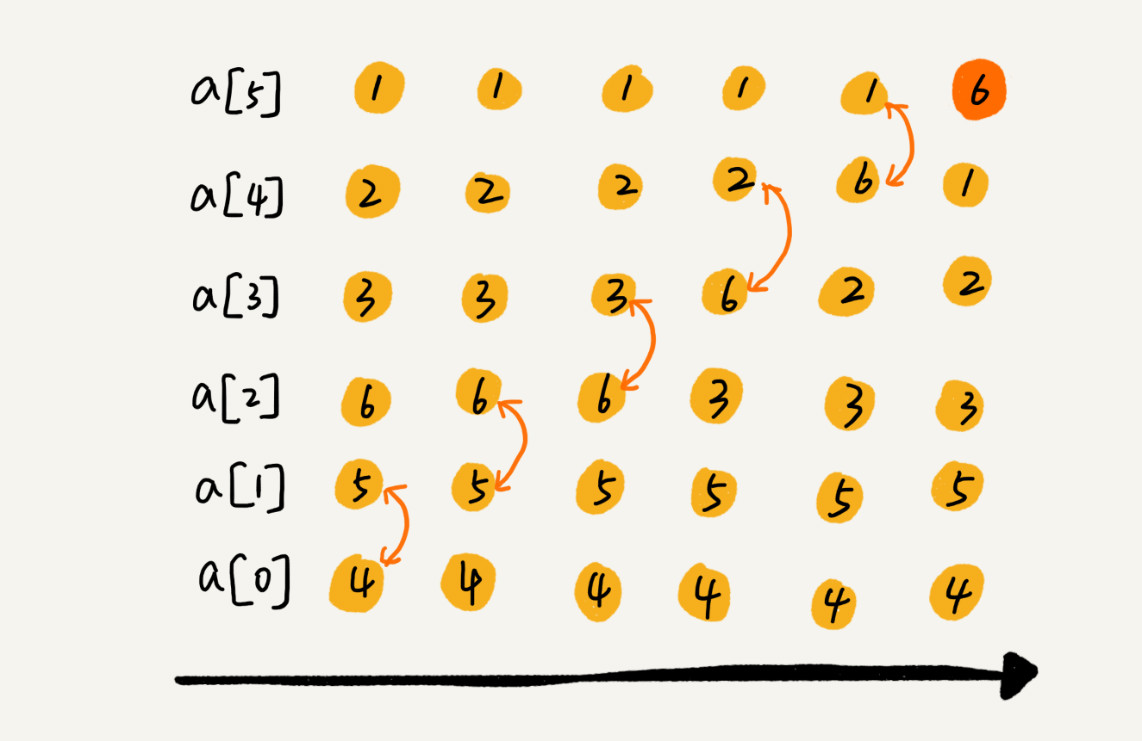
2、整个冒泡操作的过程

 

3、算法实现

 /**
     * 冒泡:从小到大排序
     * @param array
     * @return
     */
    public static int[] bubbleSort(int[] array) {
        if (array == null || array.length <= 1) {
            return array;
        }

        int tmp = 0;
        //冒泡排序，数组长度为n,只需要冒n-1次泡，即可完成排序
        //外层循环是为了控制冒泡次数的。(因为1次冒泡，能从数组中找到一个有序数)
        for (int i = 0; i < array.length-1; i++) {
            //如果在一次冒泡中未发生数字交换，则说明数组此时已经是有序了，无需再进行接下来的冒泡排序了。
            boolean already = true;
            //里层循环是每次从剩余未有序数组里找到1个最大的。
            //比如 不有序数组为[9,8,7,6,5]
            //第一次排序结果[8,7,6,5,9]，其中不有序是[8,7,6,5] , 有序是[9]
            //第二次排序结果[7,6,5,8,9], 其中不有序是[7,6,5]   , 有序是[8,9]
            //第三次排序结果[6,5,7,8,9], 其中不有序是[6,5]   ,   有序是[7,8,9]
            //第四次排序结果[5,6,7,8,9], 其中不有序是[5]   ,   有序是[6,7,8,9]
            for (int j = 0; j <= array.length-1-i;j++) {
                if(array[j]>array[j+1]){
                    tmp =array[j];
                    array[j]=array[j+1];
                    array[j+1]=tmp;
                    //有发生交换,说明此时数组还是无序状态
                    already=false;
                }
            }
            if(already){
                break;
            }
        }
        return array;
    }

4、算法分析

• 空间复杂度：原地排序，则为O(1)
• 是否为稳定排序算法：相邻两个元素大小相等，不进行交换，故是稳定排序算法。
• 时间复杂度：0(n^2)

平均情况下的时间复杂是多少呢?前面讲过，平均时间复杂度就是加权平均期望时间复杂度，分析的时候要结合概率论的知识.

有序度:是数组中具有有序关系的元素对的个数。有序元素对用数学表达式表示就是这样：

有序元素对：a[i] <= a[j], 如果i < j。

同理，对于一个倒序排列的数组，比如 6，5，4，3，2，1，有序度是 0；对于一个完全有序的数组，比如 1，2，3，4，5，6，有序度就是 n*(n-1)/2，也就是 15。我们把这种完全有序的数组的有序度叫作满有序度。

逆序度：

逆序元素对：a[i] > a[j], 如果i < j。

逆序度 = 满有序度 - 有序度

冒泡排序包含两个操作原子，比较和交换。每交换一次，有序度就加 1。不管算法怎么改进，交换次数总是确定的，即为逆序度，也就是n*(n-1)/2–初始有序度。

此例中就是 15–3=12，要进行 12 次交换操作。

对于包含 n 个数据的数组进行冒泡排序，平均交换次数是多少呢？

• 最坏情况下，初始状态的有序度是 0，所以要进行 n*(n-1)/2 次交换。
• 最好情况下，初始状态的有序度是 n*(n-1)/2，就不需要进行交换。
• 我们可以取个中间值 n*(n-1)/4，来表示初始有序度既不是很高也不是很低的平均情况。换句话说，平均情况下，需要 n*(n-1)/4 次交换操作，比较操作肯定要比交换操作多，而复杂度的上限是 O(n2)，所以平均情况下的时间复杂度就是 O(n2)。
• 这个平均时间复杂度推导过程其实并不严格，但是很多时候很实用，毕竟概率论的定量分析太复杂，不太好用。等我们讲到快排的时候，我还会再次用这种“不严格”的方法来分析平均时间复杂度。

 

三、插入排序算法

我们将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束。

1、插入排序分析

空间复杂度：O(1)

是否稳定排序算法：插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

时间复杂度：

• 最好时间复杂度O(n)
• 最坏时间复杂度O(n^2)
• 平均时间复杂度为 O(n^2)。

2、插入排序的案例

/**
     * 插入排序：从小到大
     *
     * @param array
     * @return
     */
    public static int[] insertSort(int[] array) {
        if (array == null || array.length <= 1) {
            //临界条件
            return array;
        }
        int length = array.length;

        //比如原始数组是[8,3,6,4,2,10,4]
        //第一次外层循环, 其中有序数组是[8]              待插入元素是3,      排序结果[3,8,6,4,2,10,4]
        //第二次外层循环, 其中有序数组是[3,8]            待插入元素是6,      排序结果[3,6,8,4,2,10,4]
        //第三次外层循环, 其中有序数组是[3,6,8]          待插入元素是4,      排序结果[3,4,6,8,2,10,4]
        //第四次外层循环, 其中有序数组是[3,4,6,8]        待插入元素是2,      排序结果[2,3,4,6,8,10,4]
        //第五次外层循环, 其中有序数组是[2,3,4,6,8]      待插入元素是10,     排序结果[2,3,4,6,8,10,4]
        //第六次外层循环, 其中有序数组是[2,3,4,6,8,10]   待插入元素是4,      排序结果[2,3,4,4,6,8,10]

        //默认第一个元素就是有序数组，从第二个元素开始进行插入排序
        for (int i = 1; i < length; i++) {

            int compare = array[i];//给比较元素赋值
            int j = i - 1;
            //开始从有序数字的尾巴向前找合适的位置
            for (; j >= 0; --j) {
                if (array[j] > compare) {
                    array[j + 1] = array[j];
                } else {
                    //已经找到合适位置,需要进行循环中断
                    break;
                }
            }
            array[j + 1] = compare;
        }

        return array;

    }

public static int[] insertSortArray(int[] target){
        if(target==null||target.length<=1){
            return target;
        }
        int length=target.length;
        //外层循环从第一个元素开始向后排序
        //例如 [8,4,7,9,10]从4开始向后遍历
        //第一轮遍历结果：[4,8       7,9,10]
        //第二轮遍历结果：[4,7,8     9,10]
        //第三轮遍历结果：[4,7,8,9   ,10]
        //第四轮遍历结果：[4,7,8,9,10   ]
        for(int i=1;i<length;i++){
            int tmp=0;
            //内存循环,从自身开始，向有序数组进行遍历比较
            for(int j=i;j>=1;j--){
                if(target[j]<target[j-1]){
                    tmp=target[j];
                    target[j]=target[j-1];
                    target[j-1] =tmp;
                    continue;
                }
                break;
            }
        }
        return target;
    }

四、选择排序算法

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

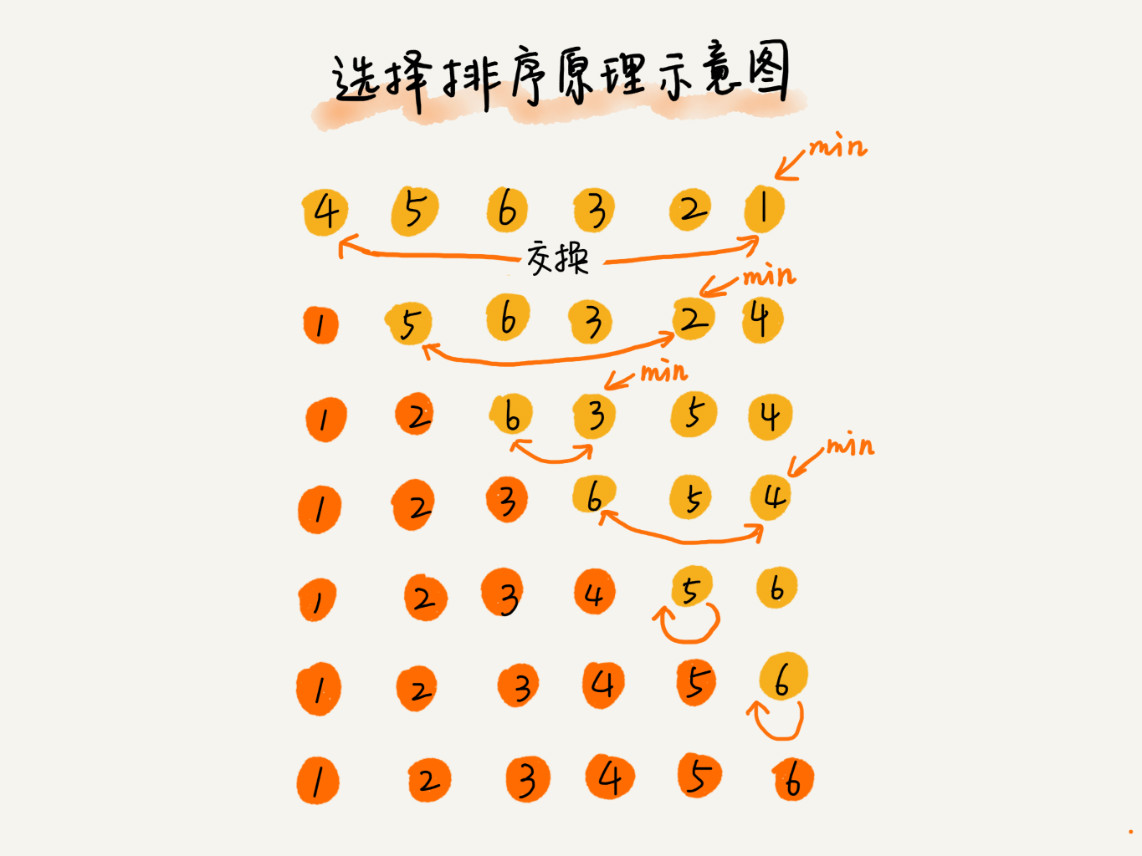
1、选择排序分析

空间复杂度:O(1)

是否稳定排序算法：不稳定排序算法;比如 5，8，5，2，9 这样一组数据，使用选择排序算法来排序的话，第一次找到最小元素 2，与第一个 5 交换位置，那第一个 5 和中间的 5 顺序就变了，所以就不稳定了。正是因此，相对于冒泡排序和插入排序，选择排序就稍微逊色了。

时间复杂度：

• 选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n2)

 

2、选择排序案例

public void selectionSort(int[] a,int n){
        if(n<=1){return ;}
        for(int i=0;i<n;i++){

            //声明最小变量为未排序空间的第一个值
            int min=a[i];
            //声明未排序空间最小值的下标
            int minIndex=i;

            for(int j=i;j<n;j++){
                //从未排序的部分找到最小值
                if(min>a[j]){
                    min=a[j];
                    minIndex=j;
                }
            }

            //将最小值放入已排序空间的最后1个位置
            int temp=a[i];
            a[i]=min;
            a[minIndex]=temp;
        }
    }

3、总结

 

如果对于链表进行排序的话，执行冒泡，插入，选择排序的如何进行

觉得应该有个前提，是否允许修改链表的节点value值，还是只能改变节点的位置。

一般而言，考虑只能改变节点位置

• 冒泡排序相比于数组实现，比较次数一致，但交换时操作更复杂；
• 插入排序，比较次数一致，不需要再有后移操作，找到位置后可以直接插入，但排序完毕后可能需要倒置链表；
• 选择排序比较次数一致，交换操作同样比较麻烦。
• 综上，时间复杂度和空间复杂度并无明显变化，若追求极致性能，冒泡排序的时间复杂度系数会变大，插入排序系数会减小，选择排序无明显变化。