【数据结构和算法】之栈
一、概念
- 栈是一种“操作受限”的线性表
- 当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出、先进后出的特性,我们就应该首选“栈”这种数据结构。
二、栈的类型
栈既可以用数组来实现,也可以用链表来实现。
- 顺序栈:用数组实现的栈
- 链式栈:用链表实现的栈
三、时间和空间复杂度
时间复杂度
入栈:O(1)
出栈:O(1)
四、算法应用
1、栈在函数调用中的应用

int main() { int a = 1; int ret = 0; int res = 0; ret = add(3, 5); res = a + ret; printf("%d", res); reuturn 0; } int add(int x, int y) { int sum = 0; sum = x + y; return sum; }
从代码中我们可以看出,main() 函数调用了 add() 函数,获取计算结果,并且与临时变量 a 相加,最后打印 res 的值。为了让你清晰地看到这个过程对应的函数栈里出栈、入栈的操作,我画了一张图。图中显示的是,在执行到 add() 函数时,函数调用栈的情况。
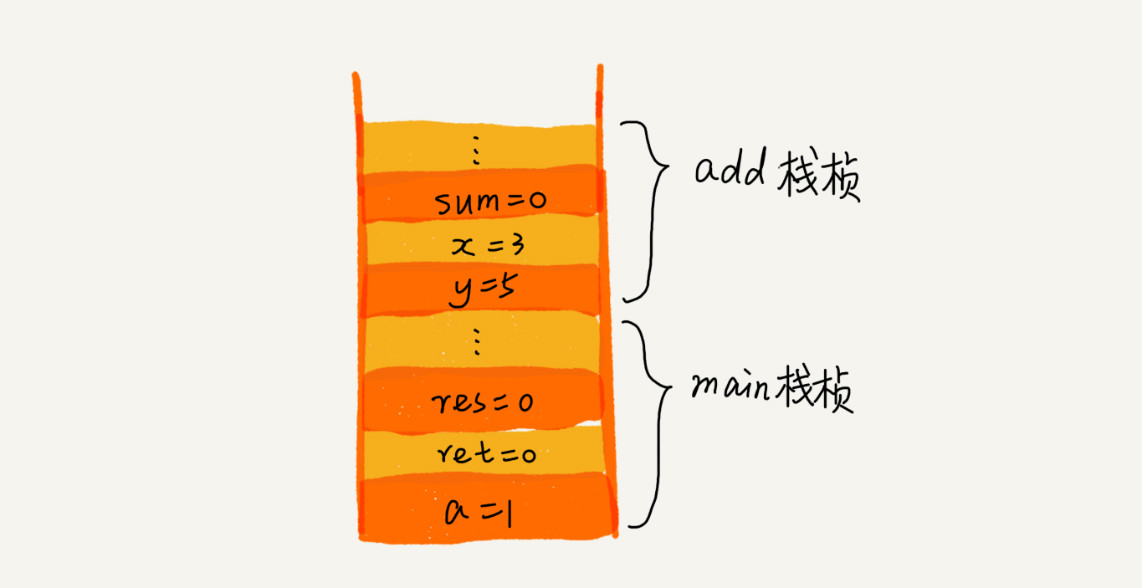
2、栈在表达式求值中的应用
我们再来看栈的另一个常见的应用场景,编译器如何利用栈来实现表达式求值。
编译器就是通过两个栈来实现的。其中一个保存操作数的栈,另一个是保存运算符的栈。我们从左向右遍历表达式,当遇到数字,我们就直接压入操作数栈;当遇到运算符,就与运算符栈的栈顶元素进行比较。
如果比运算符栈顶元素的优先级高,就将当前运算符压入栈;如果比运算符栈顶元素的优先级低或者相同,从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算完的结果压入操作数栈,继续比较。
将 3+5*8-6 这个表达式的计算过程画成了一张图,你可以结合图来理解我刚讲的计算过程。
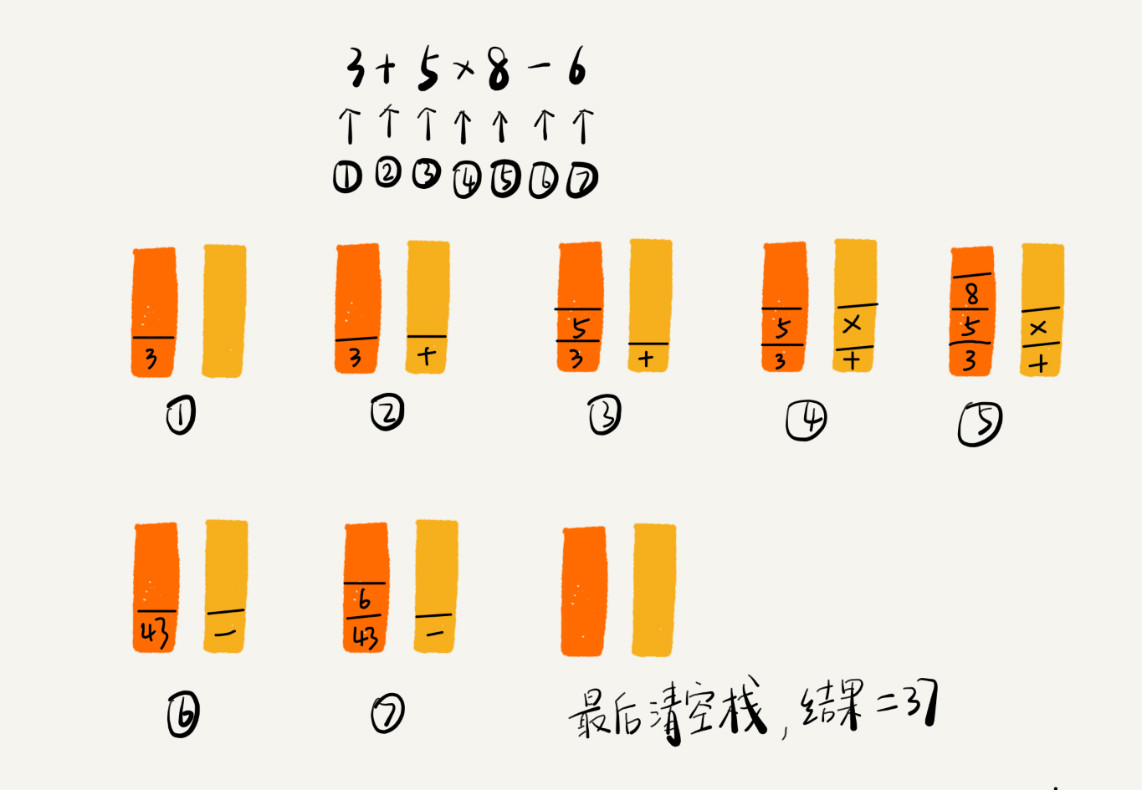
3、栈在括号匹配中的应用
我们同样简化一下背景。我们假设表达式中只包含三种括号,圆括号 ()、方括号[]和花括号{},并且它们可以任意嵌套。比如,{[] ()[{}]}或[{()}([])]等都为合法格式,而{[}()]或[({)]为不合法的格式。那我现在给你一个包含三种括号的表达式字符串,如何检查它是否合法呢?这里也可以用栈来解决。我们用栈来保存未匹配的左括号,从左到右依次扫描字符串。当扫描到左括号时,则将其压入栈中;当扫描到右括号时,从栈顶取出一个左括号。如果能够匹配,比如“(”跟“)”匹配,“[”跟“]”匹配,“{”跟“}”匹配,则继续扫描剩下的字符串。如果扫描的过程中,遇到不能配对的右括号,或者栈中没有数据,则说明为非法格式。当所有的括号都扫描完成之后,如果栈为空,则说明字符串为合法格式;否则,说明有未匹配的左括号,为非法格式。
五、栈的实现
1、数组栈

/** * count 充当计数,也充当了栈的指针 **/ public class ArrayStack { public static void main(String[] args) { ArrayStack arrayStack = new ArrayStack(10); arrayStack.putData(1); arrayStack.putData(2); arrayStack.putData(3); arrayStack.putData(4); arrayStack.putData(5); arrayStack.putData(6); arrayStack.putData(7); arrayStack.putData(8); arrayStack.putData(9); arrayStack.putData(10); try { arrayStack.putData(11); }catch (Exception e){ e.printStackTrace(); System.out.println("栈满"); } for(int i=0;i<10;i++){ System.out.println(arrayStack.pollData()); } try { arrayStack.pollData(); }catch (Exception e){ e.printStackTrace(); System.out.println("栈空"); } } //容量 private int capacity; //存储栈的数据 private int[] tab; //栈元素个数 && 担任栈的指针角色 private int count; public ArrayStack(int capacity){ this.capacity =capacity; this.count=0; this.tab = new int[capacity]; } /** * 向栈中放入一个元素 * @param data */ public void putData(int data){ //判断栈是否已经满了 if(this.count == this.capacity){ throw new IllegalArgumentException("栈满"); } //放入元素 tab[count++]=data; } public int pollData(){ //判断栈已经是空的了 if(this.count == 0){ throw new IllegalArgumentException("栈空"); } return tab[--count]; } }
2、链表栈

/** * 链表栈:尾巴节点进队,尾巴节点出队 * **/ public class LinkStack { public static void main(String[] args) { LinkStack linkStack = new LinkStack(10); linkStack.putData(1); linkStack.putData(2); linkStack.putData(3); linkStack.putData(4); linkStack.putData(5); linkStack.putData(6); linkStack.putData(7); linkStack.putData(8); linkStack.putData(9); linkStack.putData(10); try { linkStack.putData(11); }catch (Exception e){ e.printStackTrace(); System.out.println("栈满"); } for(int i=0;i<10;i++){ System.out.println(linkStack.popData()); } try { linkStack.popData(); }catch (Exception e){ e.printStackTrace(); System.out.println("栈空"); } } private final Node nodeTag = new Node(-1); private int capacity; private Node head; private Node tail; private int count; public LinkStack(int capacity){ this.capacity = capacity; this.head=this.tail = nodeTag; this.count=0; } /** * 向栈中加入元素 * @param data */ public void putData(int data){ if(count==capacity){ throw new IllegalArgumentException("栈满"); } Node node = new Node(data); if(head==tail){ head.next=node; node.pre=head; this.tail=node; }else{ this.tail.next=node; node.pre=this.tail; this.tail=node; } count++; } /** * 从栈中弹出元素 * @return */ public int popData(){ if(count==0){ throw new IllegalArgumentException("栈空"); } int result; if(tail.pre == nodeTag){ //表示,栈中只有一个元素 result = this.tail.value; this.head.next = null; this.tail = this.head; }else{ result = this.tail.value; Node pre = this.tail.pre; pre.next=null; this.tail.pre=null; this.tail = pre; } this.count--; return result; } private static class Node{ private Node pre; private Node next; private int value; public Node(int value){ this.value=value; } } }
3、数组双栈

/** * leftIndex 和 rightIndex 的指向,都是在左栈 和 右栈 认为当前位置待存储数据的位置 * =>左栈空:leftIndex==0 左栈满:leftIndex>rightIndex * =>右栈空:rightIndex = tab.length-1 右栈满:rightIndex<leftIndex * 案例没有对数据进行清空,是基于指针移动的覆盖形式完成数据的正确性。这个在实际应用时需要注意。 **/ public class DoubleStack { public static void main(String[] args) { DoubleStack doubleStack = new DoubleStack(10); doubleStack.putLeftData(1); doubleStack.putLeftData(2); doubleStack.putLeftData(3); doubleStack.putLeftData(4); doubleStack.putLeftData(5); doubleStack.putLeftData(6); doubleStack.putRightData(7); doubleStack.putRightData(8); doubleStack.putRightData(9); doubleStack.putRightData(10); try { doubleStack.putLeftData(11); }catch (Exception e){ System.out.println("左栈满"); } try { doubleStack.putRightData(12); }catch (Exception e){ System.out.println("右栈满"); } //弹栈 for(int i=0;i<6;i++){ System.out.println( doubleStack.popLeftData()); } //弹栈 for(int i=0;i<4;i++){ System.out.println( doubleStack.popRightData()); } //栈空 try { doubleStack.popLeftData(); }catch (Exception e){ System.out.println("左栈空"); } //栈空 try { doubleStack.popRightData(); }catch (Exception e){ System.out.println("右栈空"); } } /** * 存放数据的空间 */ private int[] tab; /** * 双栈共享的容量 */ private int capacity; /** * 左栈的索引 */ private int leftIndex; /** * 右栈的索引 */ private int rightIndex; public DoubleStack(int capacity ){ if(capacity<=0){ throw new IllegalArgumentException("参数异常"); } this.capacity = capacity; this.tab = new int[this.capacity]; this.leftIndex = 0; this.rightIndex = this.tab.length-1; } /** * 向左栈加入数据 * @param data */ public void putLeftData(int data){ //step1:判断栈满 if(leftIndex>rightIndex){ throw new IllegalArgumentException("左栈满"); } //step2:设置相应的数值 tab[leftIndex++]=data; } /** * 从左栈弹出数据 * @return */ public int popLeftData(){ if(leftIndex==0){ throw new IllegalArgumentException("左栈空"); } return tab[--leftIndex]; } /** * 向右栈加入数据 * @param data */ public void putRightData(int data){ //step1:判断栈满 if(rightIndex<leftIndex){ throw new IllegalArgumentException("右栈满"); } tab[rightIndex--]=data; } /** * 从右栈弹出数据 * @return */ public int popRightData(){ if(rightIndex==tab.length-1){ throw new IllegalArgumentException("右栈空"); } return tab[++rightIndex]; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号